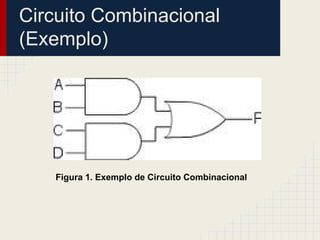
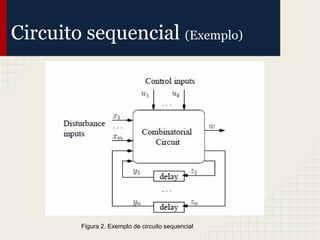
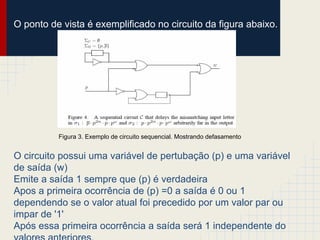
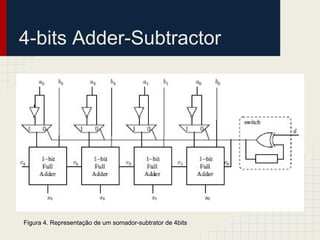
O documento discute a robustez de circuitos sequenciais. Aborda circuitos combinacionais e sequenciais, distância de Hamming e Common suffix, robustez como horizonte finito de perturbação, caracterização operacional da robustez para circuitos sequenciais e um exemplo detalhado de um somador-subtrator de 4 bits.