27-aula27.pdf

CADERNOS DE INTELIGÊNCIA ARTIFICIAL
Exemplos em Python
Prof. Ronaldo F. Ramos, Dr
24 de março de 2023
1/38

Lógica
Inferência em LPO
2/38

Instanciação Universal
Toda instância de uma sentença universalmente quantificada é
consequência lógica da mesma.
∀vα
subs({v/g}, α)
Ex. Todo Homem é Mortal tem como consequência lógica Pedro é
mortal, José é mortal, etc.
∀xHx → Mx |= Hpedro → Mpedro, Hjose → Mjose, Hjoao → Mjoao
3/38

Instanciação Existencial
Para toda sentença α , variável v e constante k que não apareça
em outro lugar na base de conhecimento.
∃vα
subs({v/k}, α)
Ex. Alguém é inteligente tem como consequência lógica A é
inteligente. Onde A é uma constante. Refere-se a alguém que não
conhecemos no momento, mas existe. É chamada de constante de
Skolem.
∃x Pessoax ∧ Inteligentex |= PessoaA ∧ InteligenteA
4/38

Proposicionalização
Seja a Base de Conhecimento (KB):
I Todos os gatos pretos são bonitos
∀xGatox ∧ Pretox → Bonitox
I Bigodinho é um gato 1
Gatobigodinho
I Bigodinho é Preto
Pretobigodinho
I Bigodinho é irmão de Orelinha
Irmaobigodinho,orelinha
1
Obrigado a Ana Vitória
5/38

Instâncias
Instanciado a quantificação universal em todas as formas possı́veis
teremos:
I Bigodinho é um gato preto bonito
Gatobigodinho ∧ Pretobigodinho → Bonitobigodinho
I O irmão de Bigodinho é um gato preto bonito
GatoIrmaobigodinho,orelinha
∧ PretoIrmaobigodinho,orelinha
→
BonitoIrmaobigodinho,orelinha
I Orelinha é um gato preto bonito
Gatoorelinha ∧ Pretoorelinha → Bonitoorelinha
I Bigodinho é um gato
Gatobigodinho
I Bigodinho é Preto
Pretobigodinho
I Bigodinho é irmão de Orelinha
Irmaobigodinho,orelinha
6/38

Proposicionalização
I Toda KB pode ser proposicionalizada de forma a preservar a
consequência lógica.
I Uma sentença básica (sem variáveis - ground) é consequência
lógica da nova KB sse ela é consequência da KB original.
I Inferência : “proposicionalizar” a KB e aplicar as perguntas,
resolução, por exemplo, e retornar os resultados.
I Problema: com funções existem infinitos termos básicos.
Ex.IrmaoIrmaoIrmao
7/38

Teorema de Herbrand (1930)
Se uma sentença α é consequência de uma KB em LPO, ela é
consequência de um subconjunto finito da KB proposicionalizada.
8/38

Loop de Redução
For n = 0 to ∞ do
I Criar uma KB proposicional instanciando com profundidade de
“n” termos
I verificar se α is consequência desta KB
9/38

Loop Infinito
Funciona se α é consequência, senão fica em loop infinito.
10/38

Teorema de Turing (1936), Church (1936)
Consequência lógica para a LPO é semidecidı́vel (Existem
algoritmos que dizem sim para toda sentença dedutı́vel, mas
nenhum algoritmo existe que diga não para toda sentença não
dedutı́vel)
11/38

Problemas
I Geração de Sentenças irrelevantes
Ex. Pretoorelinha
I Com p predicados de aridade k e n constantes teremos p ∗ nk
instâncias.
12/38

Modus Ponens Generalizado
Podemos obter uma inferência imediata se pudermos encontrar
uma substituição θ tal que Gatox e Pretox . Neste caso
encontramos Gatobigodinho e Pretobigodinho.
Logo:
θ = {x/bigodinho}
Então temos e expressão instanciada (Aplicada a substituição):
Gatobigodinho ∧ Pretobigodinho → Bonitobigodinho
Temos também:
Gatobigodinho e também Pretobigodinho Aplicando o Modos Pones
teremos como consequência:
Bonitobigodinho
Que é o que querı́amos saber...
13/38

Modus Ponens Generalizado
p10, p20, . . . , pn0, (p1 ∧ p2 ∧ . . . ∧ pn → q)
qθ
Onde, P10 pode ser algo como Gatox e P1 seria Gatobigodinho
Detalhes:
I GMP é utilizado com KB de cláusulas definidas (conjunto de
disjunções com exatamente um literal positivo)
I Todas as variáveis são universalmente quantificadas.
14/38

Unificação
Uma substituição que iguala duas expressões é chamada de
unificação e a substituição é chamada de unificador.
p q theta
Conhece(Pedro,x) Conhece(Pedro,Carla) x/Carla
Conhece(Pedro,x) Conhece(y,Bill) x/Bill, y/Pedro
Conhece(Pedro,x) Conhece(y,Mae(y)) y/Pedro,x/Mae(Pedro)
Conhece(Pedro,x) Conhece(x,OJ) = falha
Solução para conflitos :
I Padronização separada elimina sobreposição de variáveis, e.g.,
Conhece(Z17, Bill)
15/38

Unificador Mais Geral
I Para unificar Conhece(Pedro, x) e Conhece(y, z) teremos as
seguintes possibilidades,
θ = {y/Pedro, x/z}ou θ = {y/Pedro, x/Pedro, z/Pedro}
I O primeiro unificador é mais geral que o segundo.
I Existe um único Unificador Mais Geral (UMG) que é exclusivo
para renomear variáveis.
UMG = {y/Pedro, x/z}
16/38

Algoritmo de Unificação
função Unifica(x,y,temp):
I se temp = ”falhou”então retorne ”falhou”
I senão se x == y retorne temp
I senão se x é uma variável retorne UnificaVariavel(x,y,temp)
I senão se y é uma variável retorne UnificaVariável(x,y,temp)
I senão se x e y são termos compostos retorne Unifica
(argumentos[x],argumentos(y),Unifica(operando[x],operando2[y]))
I senão se x e y são listas retorne
Unifica(resto[x],resto[y],Unificar(primeiro[x],primeiro[y]))
I senão retorne ”falhou”
2
Nome da função
17/38

Funçao UnificaVariável
função UnificaVariável(var,x,temp):
I se { var/val } ∈ temp retorne Unifica(val,x,temp)
I senão se { x/val } ∈ temp retorne Unifica(var,val,temp)
I senão se verificaOcorrência(var,x) retorne ”falhou”
I senão retorne adicionar{ var/x } a temp
18/38

Uma base de conhecimento não estruturada. FONTE:
Russel and Norvig
A lei americana estabelece que é crime um americano vender
armas para nações hostis. O paı́s Nono, um inimigo dos EUA, tem
alguns mı́sseis, e todos estes mı́sseis foram vendidos pelo coronel
West, que é americano.
Coronel West é criminoso?
19/38

Encadeamento Pra Frente
Conforme já vimos, o encadeamento pra frente se dá pela aplicação
de Modus Ponens sucessivos sobre expressões na forma de cláusulas
definidas. Vejamos alguns exemplos de cláusulas definidas.
20/38

Formalizando em Cláusulas Definidas]
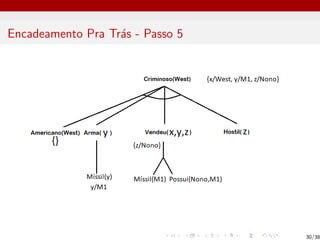
I É um crime para um americano vender armas para nações
hostis
Americanox ∧ Armay ∧ Vendeux,y,z ∧ Hostilz → Criminosox
I Nono tem alguns mı́sseis
PossuiNono,M1
MissilM1
I Todos os mı́sseis foram vendidos pelo coronel West
Missilx ∧ PossuiNono,x → VendeuWest,x,Nono
I Mı́sseis são armas
Missilx → Armax
21/38

Formalizando em Cláusulas Definidas]
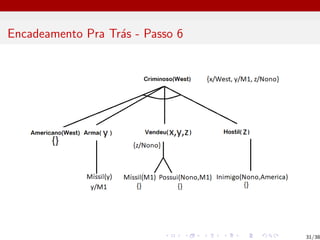
I Um inimigo da América é hostil
Inimigox,America → Hostilx
I West é americano
AmericanoWest
I Nono é inimigo da América
InimigoNono,America
Esta base de conhecimento é conhecida como Datalog (Cláusulas
definidas em lógica de primeira ordem sem funções)
22/38

Encadeamento Para a Frente - Passo 1
23/38

24/38

25/38

Encadeamento Pra Trás - Passo 1
26/38

27/38

28/38

29/38

30/38

31/38

Propriedades do Encadeamento Pra Frente
I Consistente e completo para LPO com cláusulas definidas.
I EF conclui um Datalog em um número finito de iterações.
I Em geral não termina se α não é consequência
lógica(semidescidı́vel).
I Casamento pode ser complicado (NP-HARD)
I Utilizado em bancos de dados dedutivos.
I Pode ser feito de forma incremental
32/38

Propriedades do Encadeamento Pra Trás
I Busca recursiva em profundidade: espaço linear no tamanho
da prova.
I Incompleta (loops infinitos)(corrige-se checando a meta atual
em relação com todas as metas na pilha).
I Em geral não termina se α não é consequência
lógica(semidescidı́vel).
I Ineficiente devido a sub metas repetidas. (Corrige-se
colocando os resultados prévios em uma cache (espaço extra))
I Muito usada em programação lógica
33/38

Resolução
Versão em primeira ordem.
l1 ∧ ... ∧ lk m1 ∧ ... ∧ mn
(l1 ∧ ... ∧ li−1 ∧ li+1 ∧ lk ∧ m1 ∧ mj−1 ∧ mj+1 ∧ ... ∧ ...mn)θ
Onde Unifica(li , ¬mj ) = θ
34/38

Resolução
Considera-se que as duas cláusulas foram padronizadas em
separado de forma que elas não compartilham variáveis.
¬Ricox ∧ Infelizx RicoKen
InfelizKen
Com θ = {x/Ken}.
Aplicar passos de resolução a FNC(KB ∧ ¬α); completo para LPO
35/38

Conversão para a forma Normal Conjuntiva
Convertendo a expressão: Todo Mundo que ama os animais é
amado por alguém.
∀x(∀yAnimaly → Amax,y ) → (∃yAma(y, x))
I Eliminar bicondicionais e implicações
∀x(¬∀y¬Animaly ∨ Amax,y ) ∨ (∃yAmay,x )
I Mover ¬ pra dentro: ¬∀xP ≡ ∃x¬P, ¬∃xP ≡ ∀x¬P
∀x(∃y¬(¬Animaly ∨ Amax,y )) ∨ (∃yAmay,x )
∀x(∃yAnimaly ∧ ¬Amax,y ) ∨ (∃yAmax,y )
∀x(∃yAnimaly ∨ ¬Amax,y ) ∨ (∃Amax,y )
I Padronização de Variáveis (Cada quantificador usa uma
variável diferente).
∀x(∃yAnimaly ∨ ¬Amax,y ) ∨ (∃zAmaz,x )
36/38

Conversão para a forma Normal Conjuntiva - Cont
I Skolemizar: uma forma mais geral de instanciação existencial.
Cada variável é substituı́da por uma função de Skolem das
variáveis quantificadas universalmente.
∀x(AnimalF(x) ∨ ¬Amax,F(x)) ∨ AmaG(x),x
I Desprezar quantificadores universais.
(AnimalF(x) ∨ ¬Amax,F(x)) ∨ AmaG(x),x
I Distribuir ∨ sobre o ∧
(AnimalF(x) ∨ AmaG(x),x ) ∧ (¬Amax,F(X) ∨ AmaG(x),x )
Voilà.
37/38

27-aula27.pdf

Mais conteúdo relacionado

Semelhante a 27-aula27.pdf

Mais de ronaldo ramos

Último

27-aula27.pdf