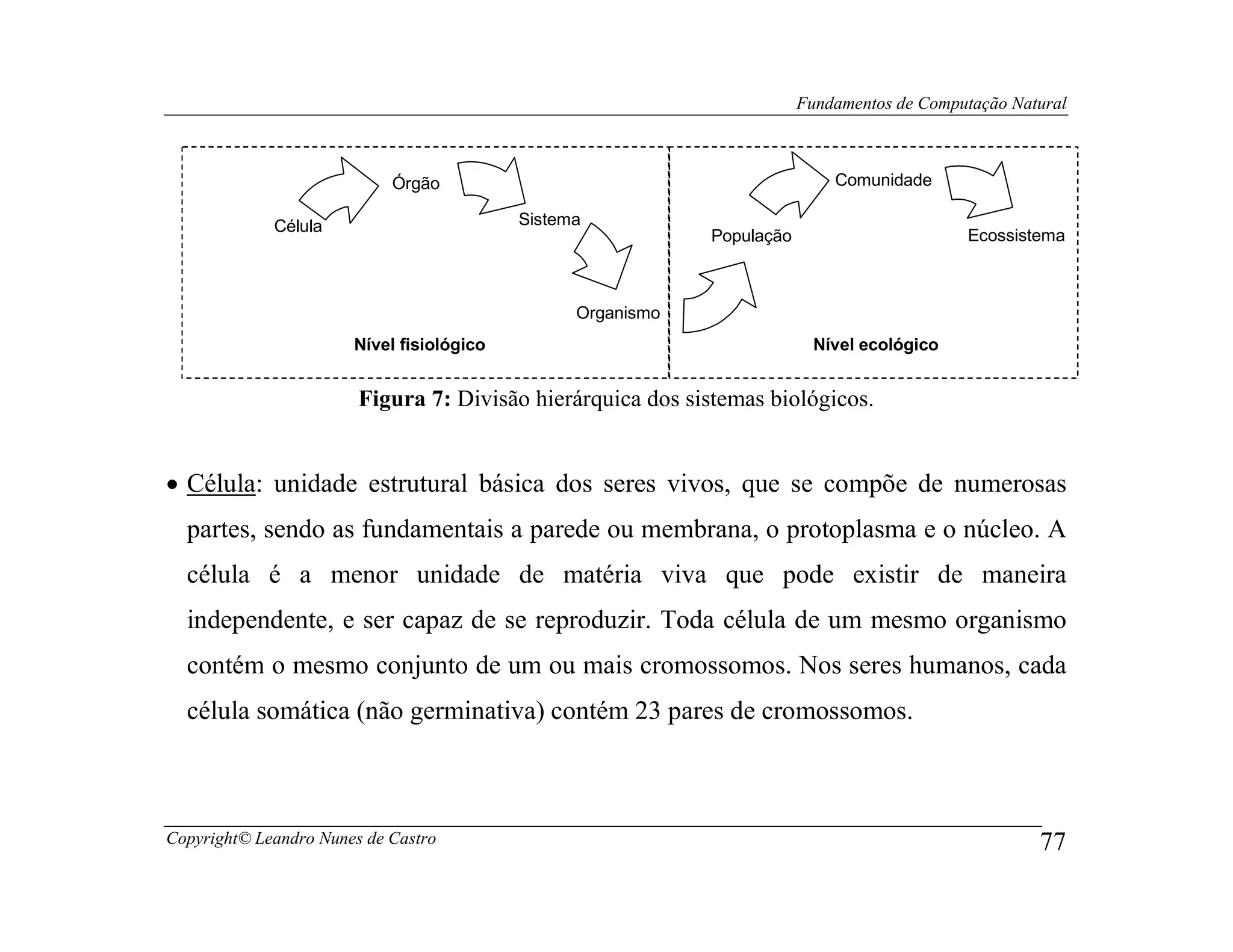
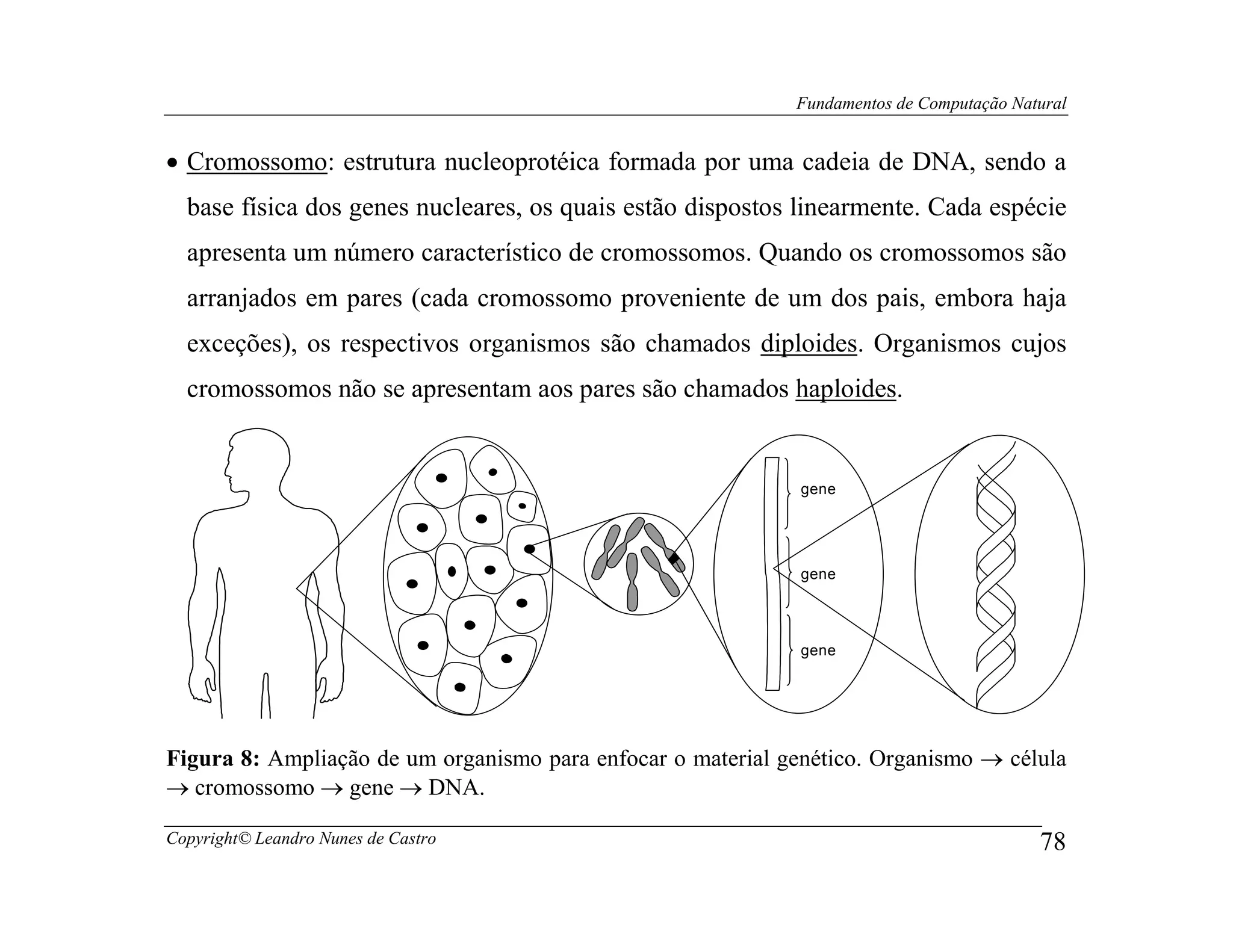
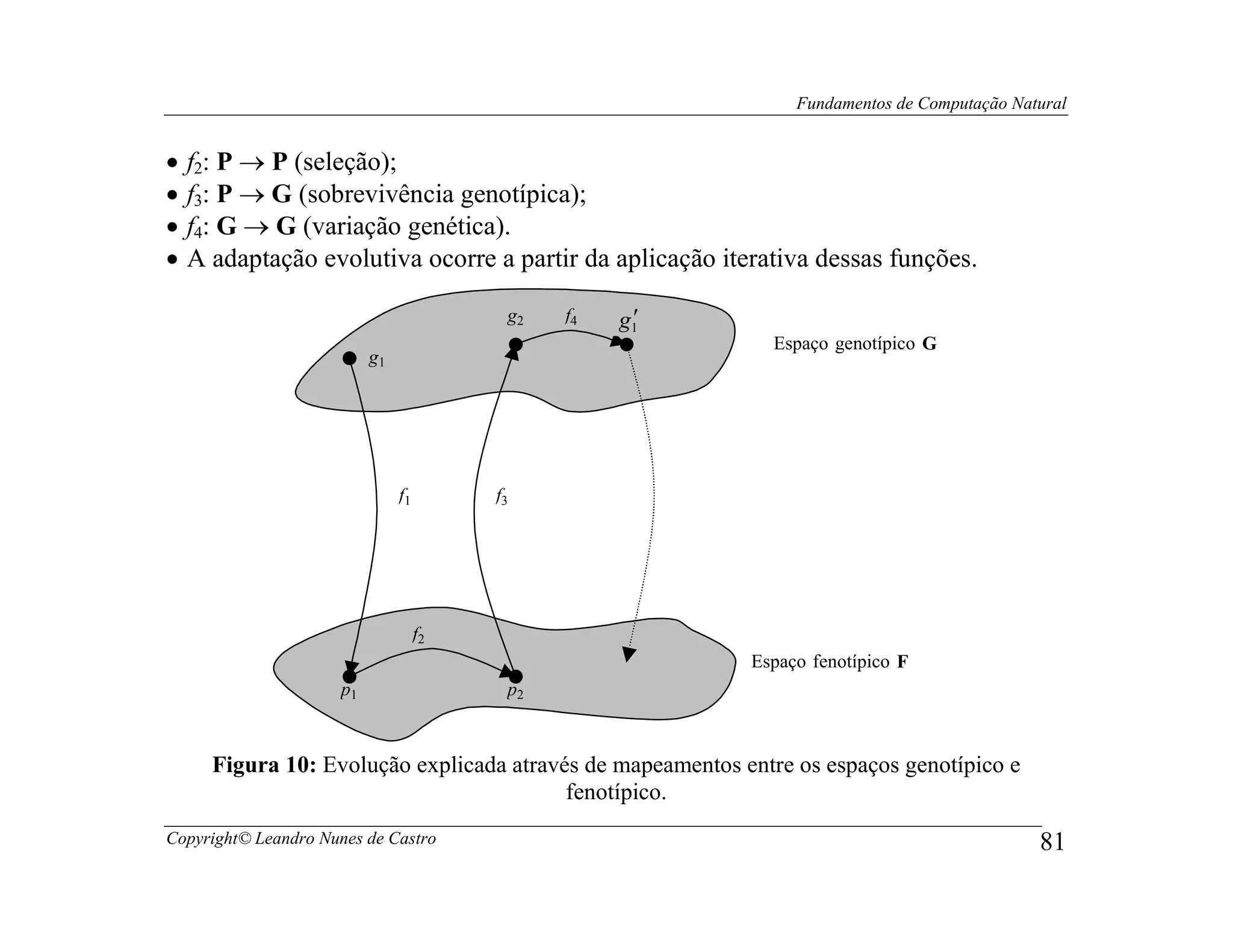
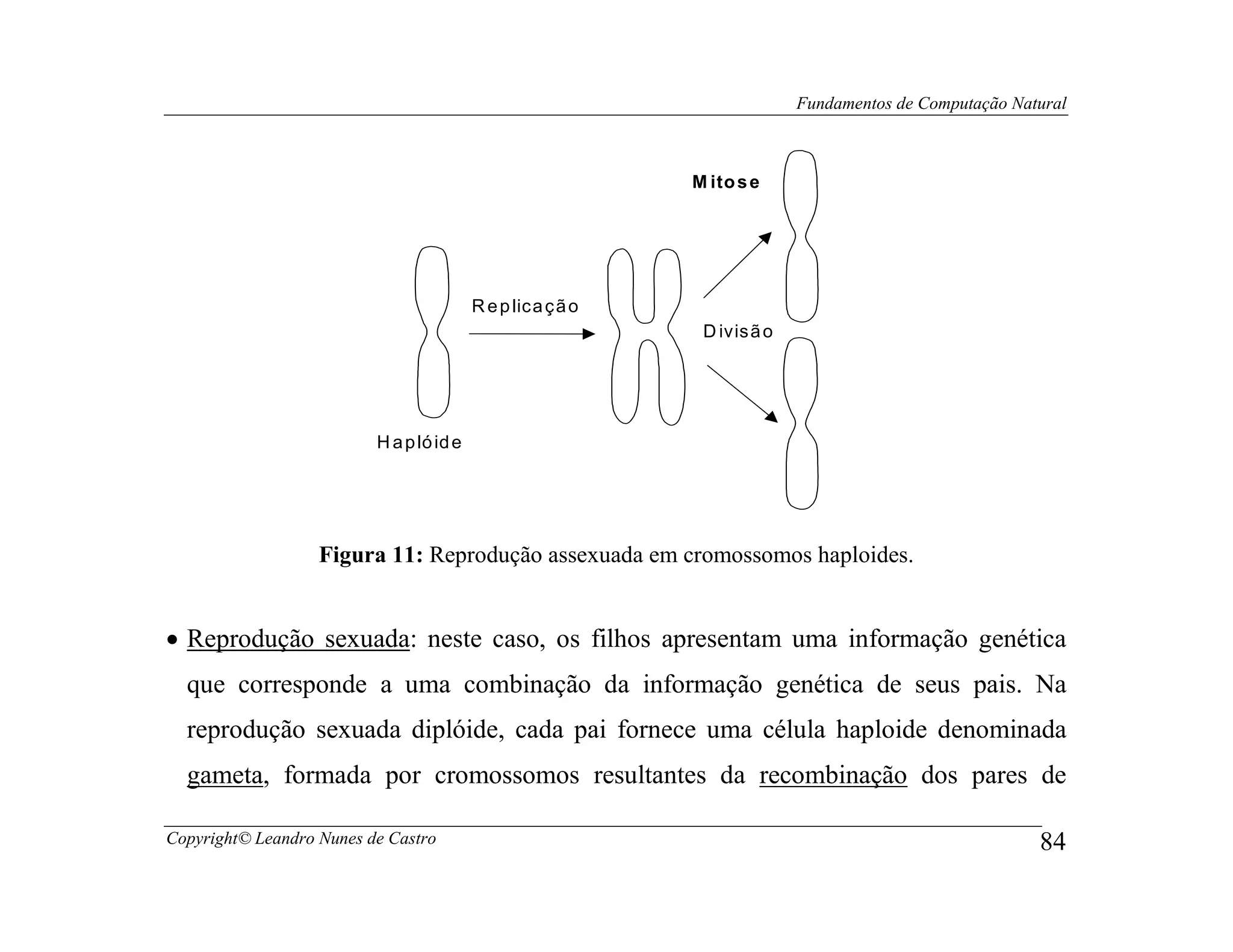
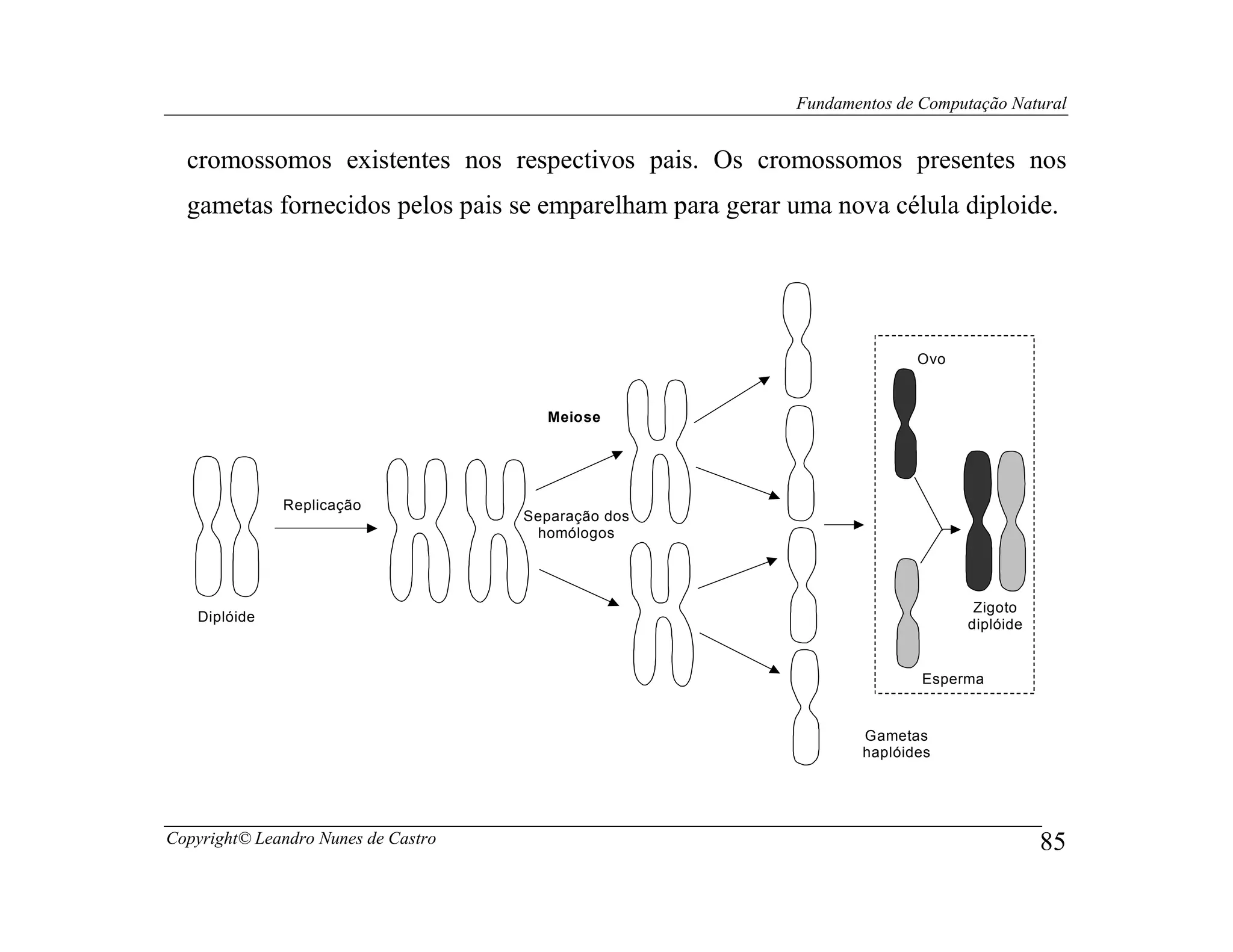
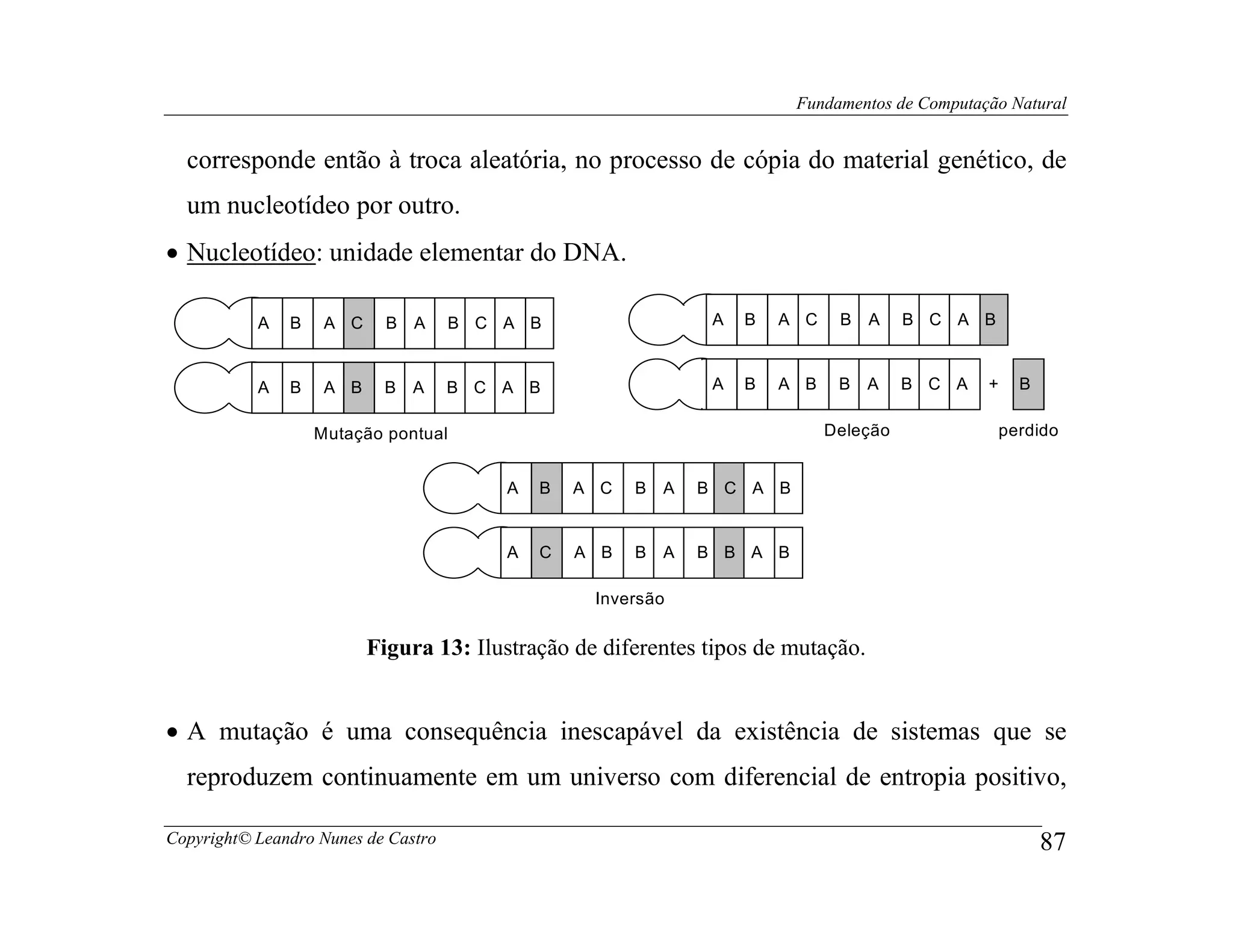
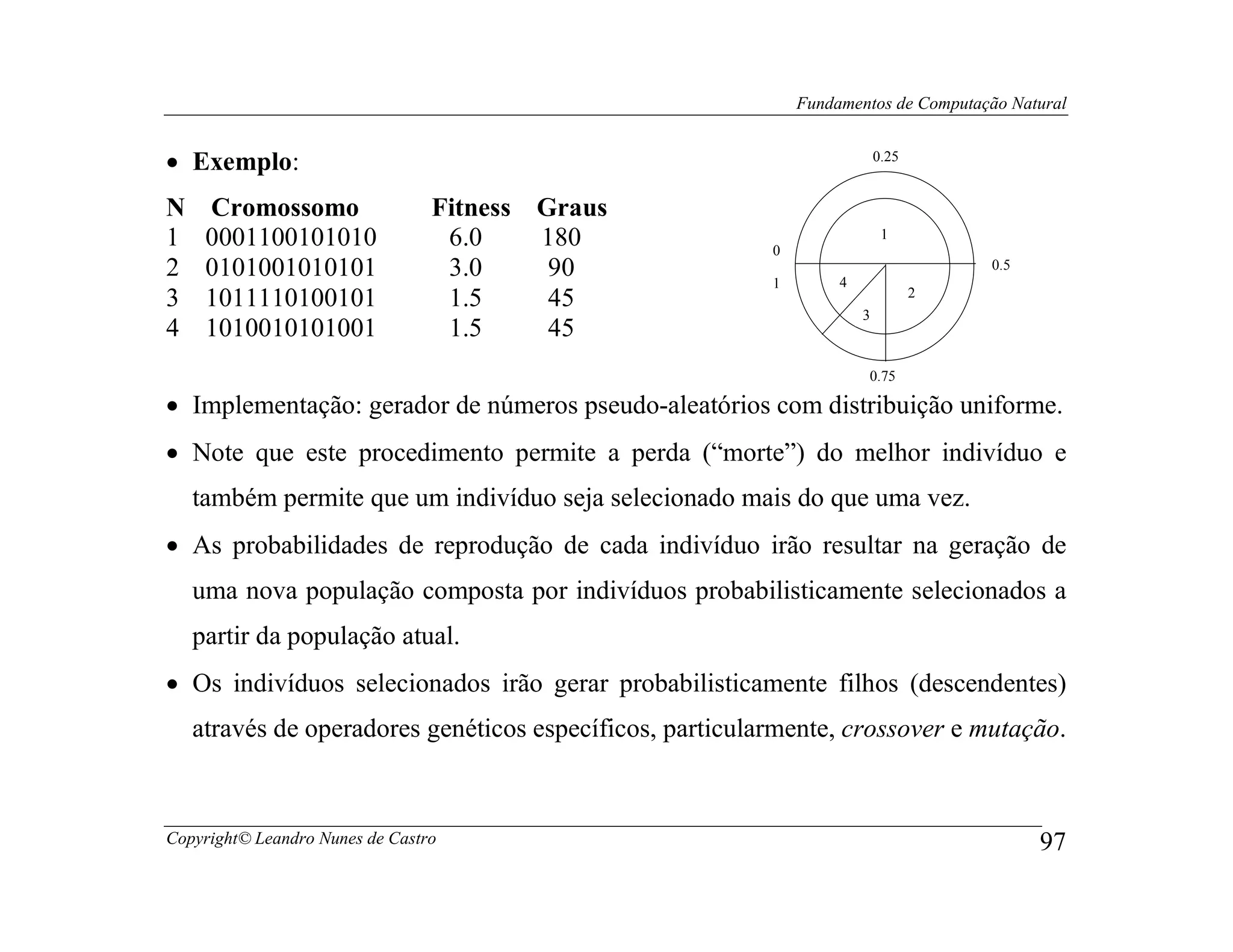
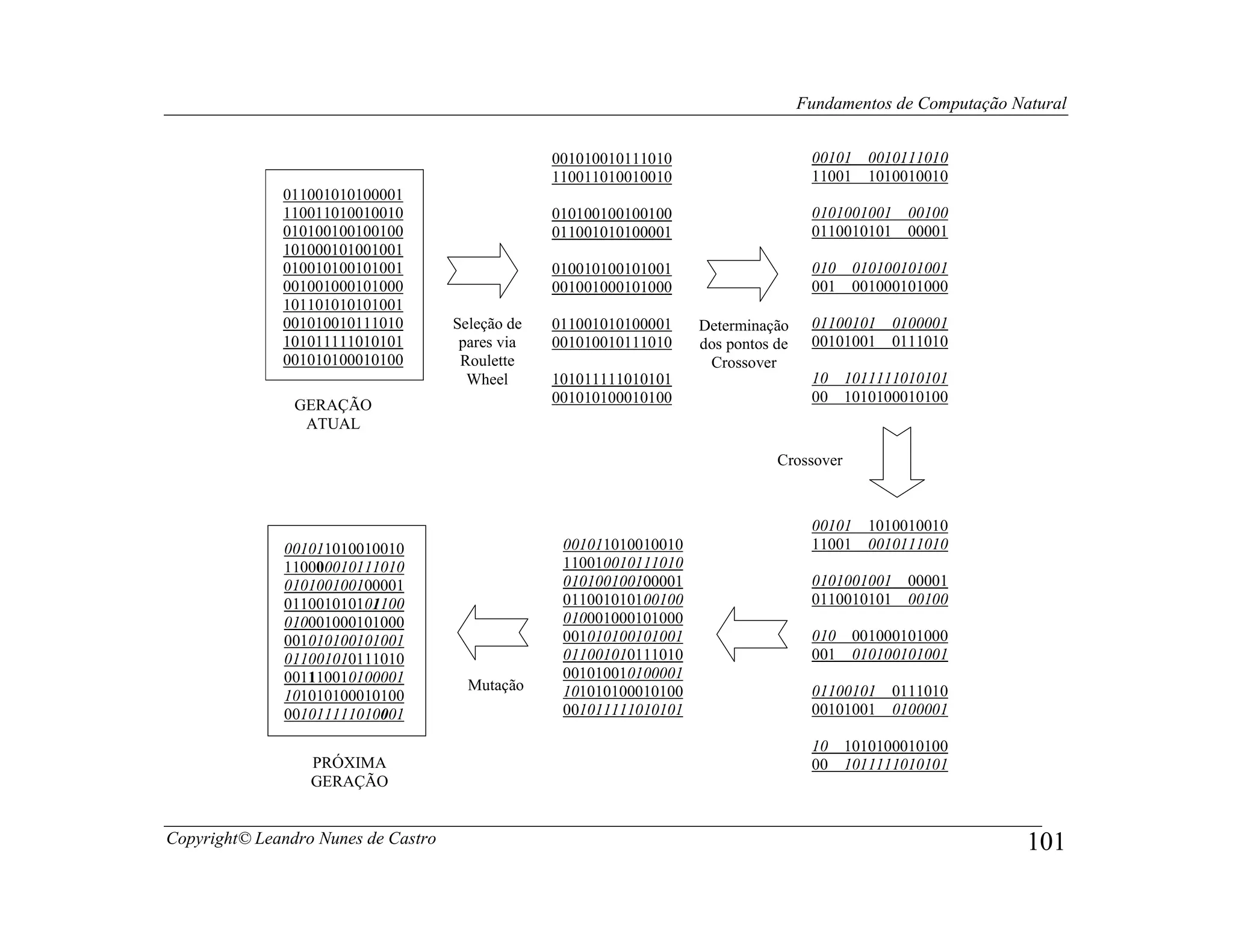
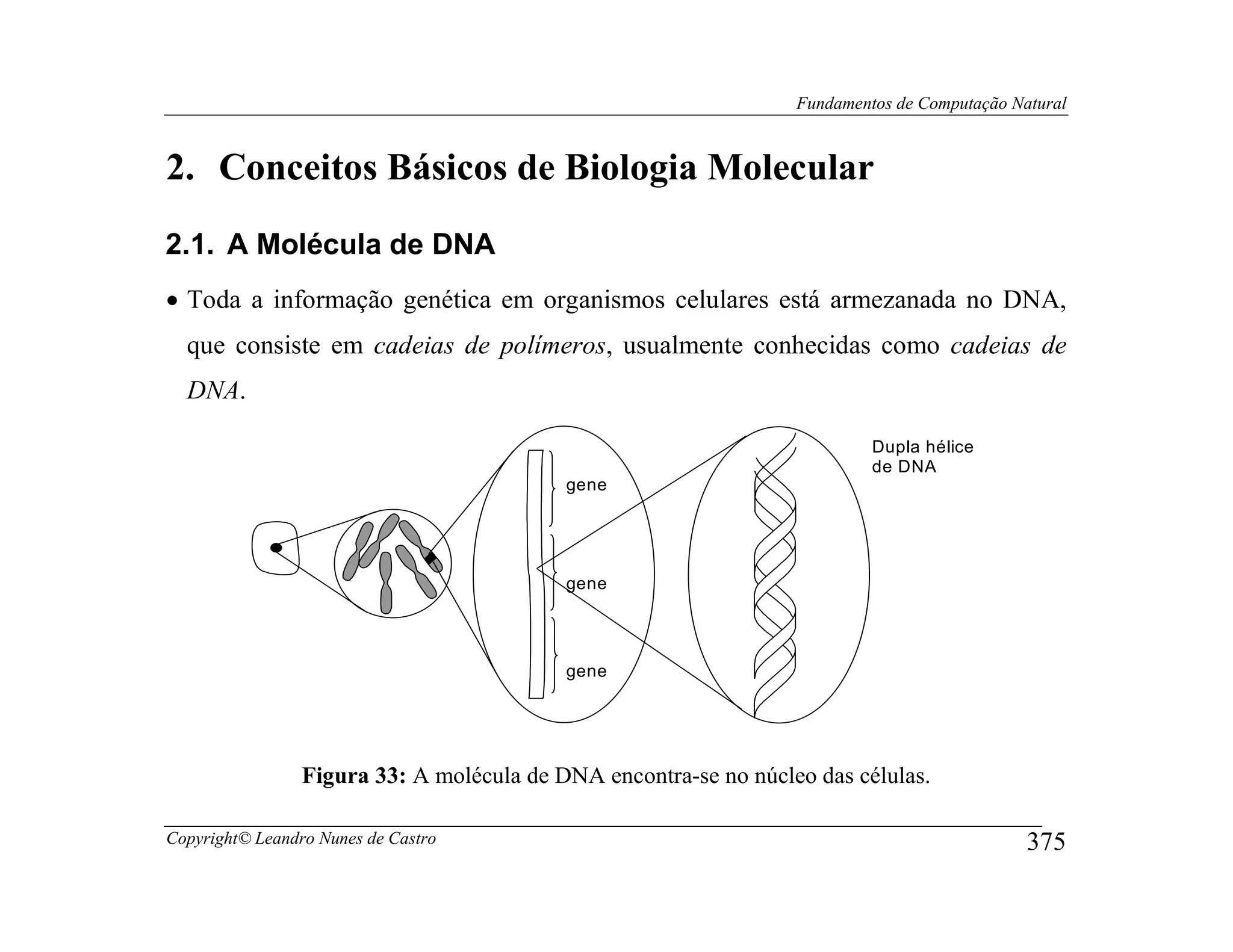
Este documento apresenta os fundamentos da computação natural, abordando tópicos como computação evolutiva, redes neurais artificiais, inteligência de enxame, geometria fractal e vida artificial. O documento também fornece uma introdução à computação de DNA e computação quântica.




















































































![Fundamentos de Computação Natural
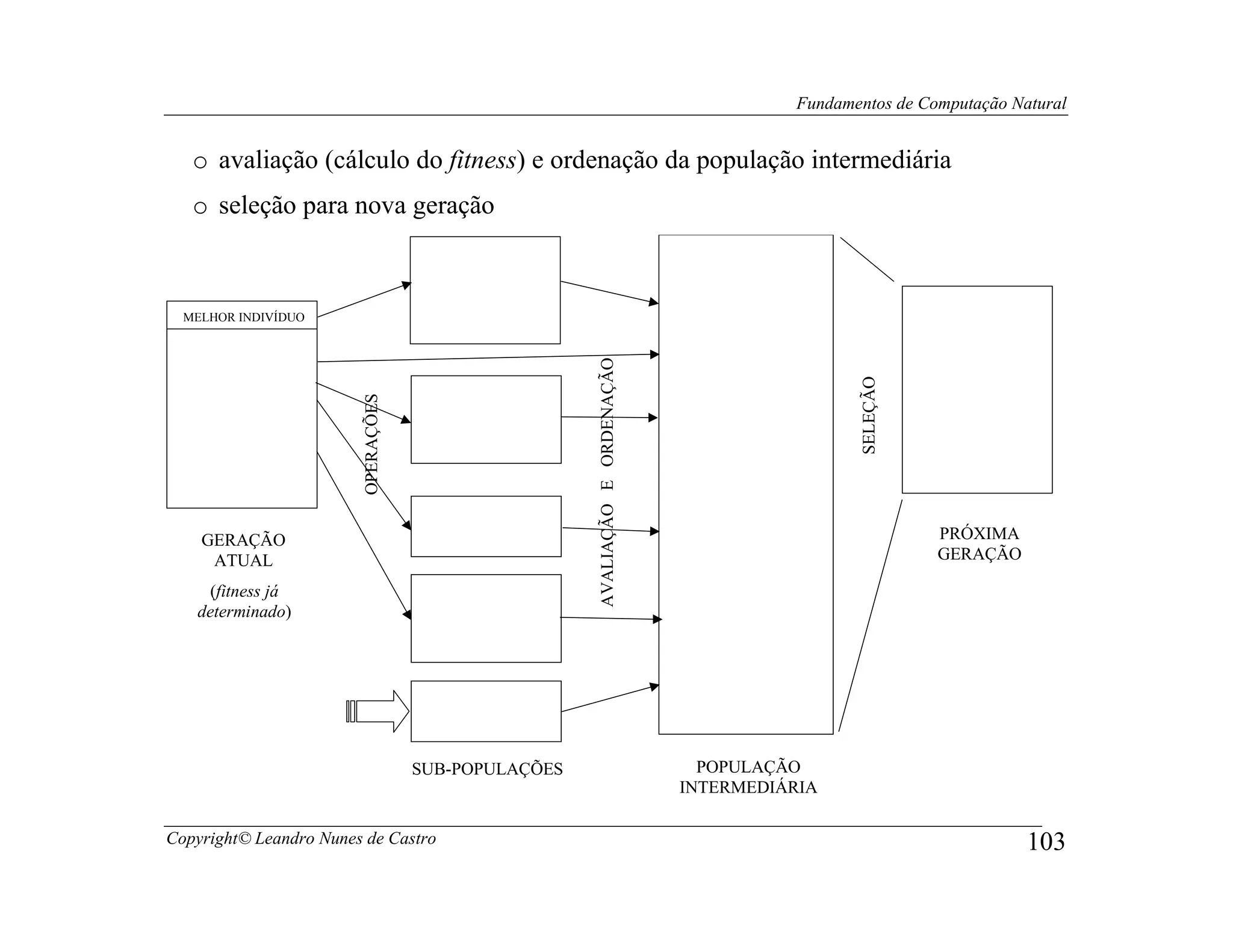
• Especificação de um objetivo
o Descrição de uma meta. Trata-se de uma expressão (e não uma função)
matemática que descreve o problema.
• Definição de uma função de avaliação
o Função que retorna um valor específico indicando a qualidade (relativa) de
uma solução candidata particular, dada a representação adotada. Trata-se
geralmente de um mapeamento do espaço de soluções candidatas, dada a
representação adotada, para um conjuto de números, onde cada elemento do
espaço de soluções candidatas possui um valor numérico indicativo de sua
qualidade. Geralmente o objetivo sugere uma função de avaliação particular.
• Exemplo: Suponha que seu objetivo seja maximizar a seguinte função de uma
2
−2 (( x − 0.1) / 0.9 )
única variável: g ( x) = 2 sen(5πx) 6 , x ∈ [0,1].
Copyright© Leandro Nunes de Castro 91](https://image.slidesharecdn.com/computacaonaturalfull-120823094923-phpapp02/75/2012-Computacao-Natural-Slides-do-Curso-91-2048.jpg)
![Fundamentos de Computação Natural
o Representação: suponha também que você irá representar a variável x
utilizando uma cadeia binária de comprimento l. Sendo assim, o espaço de
busca corresponde a todas as cadeias binárias de comprimento l, e portanto
possui dimensão 2l.
o Objetivo: max g(x), x ∈ [0,1].
o Função de avaliação: a avaliação da própria função serve para indicar a
qualidade relativa dos candidatos a solução.
1.1 Definição de um Problema de Busca
• Dado um espaço de busca S e uma região F factível deste espaço, F ⊆ S, encontre
x ∈ F tal que
eval(x*) ≤ eval(x), ∀x ∈ F
• Trata-se assim, de um problema de minimização, onde valores menores de x são
considerados de qualidade superior.
Copyright© Leandro Nunes de Castro 92](https://image.slidesharecdn.com/computacaonaturalfull-120823094923-phpapp02/75/2012-Computacao-Natural-Slides-do-Curso-92-2048.jpg)


















































![Fundamentos de Computação Natural
• Seja X ∈ ℜm×N, a matriz de dados de entradas com N padrões de dimensão m cada
(colunas de X), e d ∈ ℜ1×N o vetor de saídas desejadas. O algoritmo abaixo pode
ser utilizado para treinar o perceptron de um único neurônio:
procedure [w] = perceptron(max_it,E,α,X,d)
initialize w // por simplicidade, inicialize com 0
initialize b //por simplicidade, inicialize com 0
t ← 1
while t < max_it & E > 0 do,
for i from 1 to N do, //para cada padrão de entrada
yi ← f(wxi + b) //determine a saída para xi
ei ← di − yi //determine o erro para xi
w ← w + α ei xi //atualize o vetor de pesos
b ← b + α ei //atualize o bias
end for
E ← sum(ei)
t ← t + 1
end while
end procedure
Copyright© Leandro Nunes de Castro 157](https://image.slidesharecdn.com/computacaonaturalfull-120823094923-phpapp02/75/2012-Computacao-Natural-Slides-do-Curso-157-2048.jpg)
![Fundamentos de Computação Natural
Exemplo de Aplicação e Motivação Geométrica
• Considere o problema de utilizar o perceptron com um único neurônio para
representar a função lógica AND.
Entradas Saídas (0,1) (1,1)
x1 x2 x1 AND x2
0 0 0
0 1 0
1 0 0
1 1 1 (0,0) (1,0)
0 0 1 1
X= d = [0 0 0 1]
0 1 0 1
• A saída yi do neurônio para o vetor de dados xi pode ser representada na forma:
yi = f(wxi + b)
• Para quaisquer valores de w e b, a função f(u) separa o espaço de entradas em duas
regiões, sendo que a curva de separação (superfície de decisão) é uma linha reta.
Copyright© Leandro Nunes de Castro 158](https://image.slidesharecdn.com/computacaonaturalfull-120823094923-phpapp02/75/2012-Computacao-Natural-Slides-do-Curso-158-2048.jpg)
![Fundamentos de Computação Natural
• A equação desta reta é dada por:
w1 x1 + w2 x2 + b = 0
• Se a função de ativação do tipo sinal (degrau) possui θ = 0, então
w1 x1 + w2 x2 + b ≥ 0
resultará em uma saída positiva da rede.
• Inicializando todos os pesos e o limiar em zero w = [0 0] e b = 0, e definindo
α = 1, o algoritmo de treinamento do perceptron fornece o seguinte:
w1 = 2; w2 = 1; b = − 3, portanto 2x1 + 1x2 − 3 = 0.
• Obs.: note que os pesos do perceptron também poderiam ter sido inicializados com
valores aleatórios pequenos.
o Neste caso, a superfície de decisão obtida seria diferente.
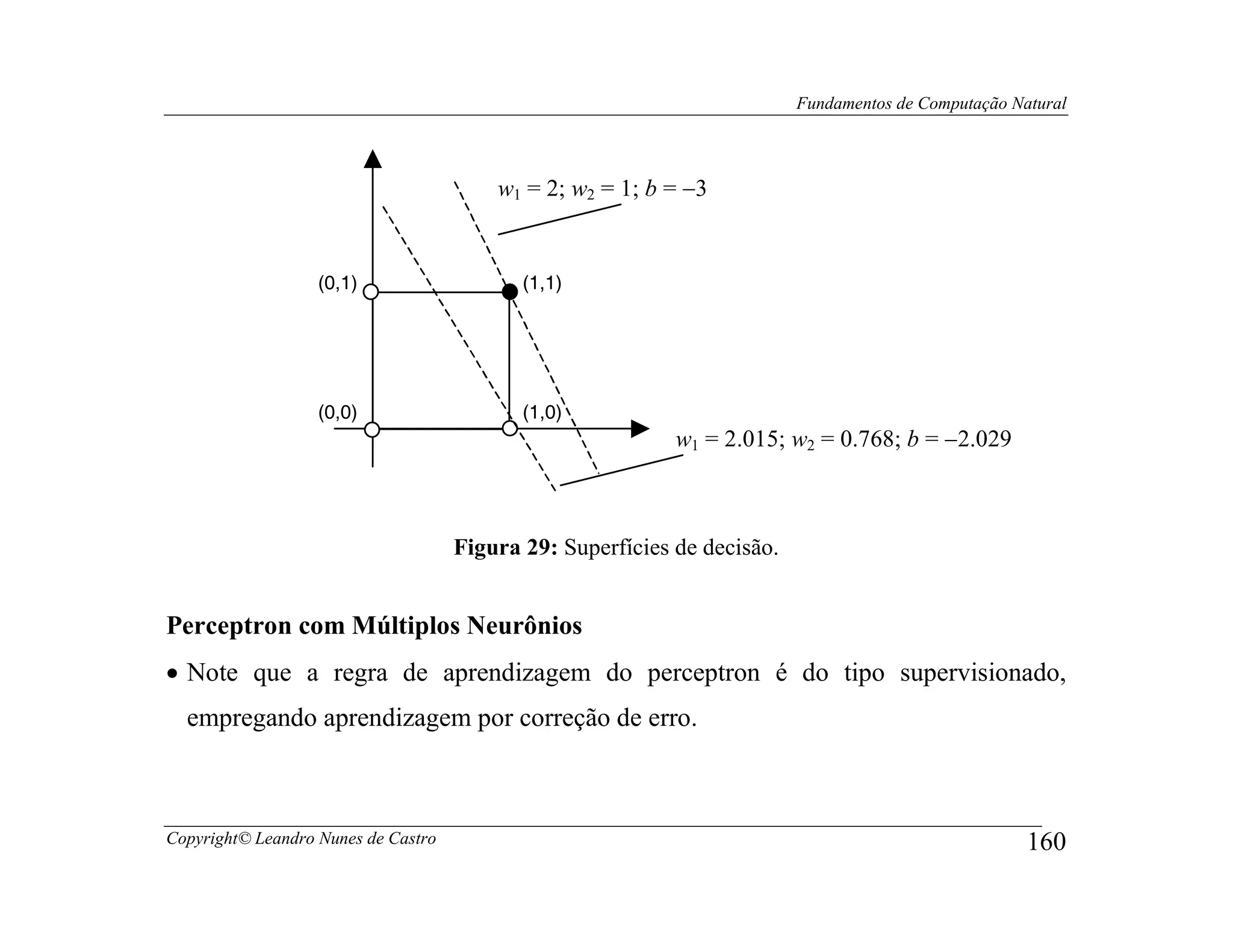
o Considere para efeitos ilustrativos: w1 = 0.015; w2 = 0.768; b = 0.971.
o A figura a seguir mostra as duas superfícies de decisão e os pesos e bias
determinados pelo algoritmo de treinamento do perceptron.
Copyright© Leandro Nunes de Castro 159](https://image.slidesharecdn.com/computacaonaturalfull-120823094923-phpapp02/75/2012-Computacao-Natural-Slides-do-Curso-159-2048.jpg)
![Fundamentos de Computação Natural
• Esta regra pode ser facilmente estendida para atualizar os pesos de uma rede de
neurônios em uma única camada.
• Neste caso, para cada vetor de entrada xi haverá um vetor de saídas da rede:
yi = f(Wxi + b); W ∈ ℜo×m, xi ∈ ℜm×1, i = 1,…,N, yi ∈ ℜo×1, e b ∈ ℜo×1, D ∈ ℜo×N.
• Existe agora um vetor de erros para cada padrão de entrada: ei = di − yi.
procedure [W] = perceptron(max_it,α,X,D)
initialize W //for simplicity set it to zero
initialize b //for simplicity set it to zero
t ← 1
while t < max_it do,
for i from 1 to N do, //para cada padrão de entrada
yi ← f(Wxi + b) //determine a saída da rede para xi
ei ← di − yi //determine o vetor de erros para xi
T
W ← W + α ei xi //atualize a matriz de pesos
b ← b + α ei //atualize o vetor de bias
end for
t ← t + 1
end while
end procedure
Copyright© Leandro Nunes de Castro 161](https://image.slidesharecdn.com/computacaonaturalfull-120823094923-phpapp02/75/2012-Computacao-Natural-Slides-do-Curso-161-2048.jpg)



![Fundamentos de Computação Natural
procedure [y] = perceptron(W,b,Z)
for i from 1 to N do, //para cada padrão de entrada xi
yi ← f(Wxi + b) //determine as saídas da rede
end for
end procedure
Copyright© Leandro Nunes de Castro 165](https://image.slidesharecdn.com/computacaonaturalfull-120823094923-phpapp02/75/2012-Computacao-Natural-Slides-do-Curso-165-2048.jpg)






















![Fundamentos de Computação Natural
procedure [best] = ACO(max_it)
initialize τij //usually every edge is initialized with the same τ0
place each ant k on a randomly selected edge
t ← 1
while t < max_it do,
for i = 1 to N do, //for each ant
build a solution by applying a probabilistic transition
rule (e − 1) times. The rule is a function of τ and η
//e is the number of edges on the graph G
end for
eval the cost of every solution built
if an improved solution is found,
then update the best solution found
end if
update pheromone trails
t ← t + 1
end while
end procedure
Copyright© Leandro Nunes de Castro 190](https://image.slidesharecdn.com/computacaonaturalfull-120823094923-phpapp02/75/2012-Computacao-Natural-Slides-do-Curso-190-2048.jpg)

![Fundamentos de Computação Natural
• Como no caso do TSP cada cidade não deve ser visitada mais do que uma vez, é
preciso armazenar informação sobre as cidades que já foram visitadas. Isso pode
ser feito empregando-se, por exemplo, uma lista tabu ou memória, que irá definir o
conjunto de cidades Jik que a formiga k ainda deve visitar enquanto na cidade i.
• A probabilidade de uma formiga k ir de uma cidade i para uma cidade j na iteração
t é dada pela seguinte regra de transição:
[τ ij (t )]α .[ηij ]β
se j ∈ J ik
pij (t ) = ∑ k [τ il (t )]α .[ηil ]β
k
l∈J i
0 caso contrário
onde τij(t) é o nível de feromônio na conexão (i,j), e ηij é a visibilidade da cidade j
quando na cidade i. Os parâmetros α e β são definidos pelo usuário e controlam o
peso relativo da intensidade da trilha (feromônio) e da visibilidade. Por exemplo, se
α = 0 cidades mais próximas tenderão a serem escolhidas, enquanto se β = 0, apenas
amplificação na quantidade de feromônio será considerada.
Copyright© Leandro Nunes de Castro 192](https://image.slidesharecdn.com/computacaonaturalfull-120823094923-phpapp02/75/2012-Computacao-Natural-Slides-do-Curso-192-2048.jpg)


![Fundamentos de Computação Natural
procedure [best] = AS-TSP(max_it)
initialize τij //usually every edge is initialized with the same τ0
place each ant k on a randomly selected city
Let best be the best tour found from the beginning and Lbest its length
t ← 1
while t < max_it do,
for i = 1 to N do, //for every ant
build tour T (t) by applying (e − 1) times the following step:
k
At city i, choose the next city j with a given probability
end for
eval the length of the tour performed by each ant
if a shorter tour is found, then update best and Lbest end if
for every city e do,
Update pheromone trails by applying the rule:
τij(t+1) ← (1−ρ)τij(t) + ∆τij(t) + b.∆τbij(t), where
∆τij(t) = ∑k ∆τkij(t), k = 1,…N;
Q / Lk (t ) if (i, j ) ∈ T k (t )
∆τ ij (t ) =
k
, and
0 otherwise
Q / Lbest if (i, j ) ∈ best
∆τ b (t ) =
ij .
0 otherwise
end for
t ← t + 1
end while
end procedure
Copyright© Leandro Nunes de Castro 195](https://image.slidesharecdn.com/computacaonaturalfull-120823094923-phpapp02/75/2012-Computacao-Natural-Slides-do-Curso-195-2048.jpg)










![Fundamentos de Computação Natural
procedure [] = ACA(max_it,N,k1,k2)
place every item i on a random cell of the grid
place every ant k on a random cell of the grid unoccupied by
ants
t ← 1
while t < max_it do,
for i = 1 to N do, //for every ant
if unladen ant AND cell occupied by item xi, then
compute f(xi) and pp(xi)
pick up item xi with probability pp(xi)
else if ant carrying item xi AND cell empty, then
compute f(xi) and pd(xi)
deposit (drop) item xi with probability pd(xi)
end if
move to a randomly selected neighboring and unoccupied
cell
end for
t ← t + 1
end while
print location of items
end procedure
Copyright© Leandro Nunes de Castro 206](https://image.slidesharecdn.com/computacaonaturalfull-120823094923-phpapp02/75/2012-Computacao-Natural-Slides-do-Curso-206-2048.jpg)



































![Fundamentos de Computação Natural
(Versão para Maximização)
procedure [X] = PSO(max_it,ϕ1,ϕ2,vmax)
initialize X //usually every particle xi is initialized at random
initialize vi //at random, vi ∈ [-vmax,vmax]
t ← 1
while t < max_it do,
for i = 1 to N do, //for each particle
if f(xi) > f(pi),
then pi = xi, //best individual performance so far
end if
for j = indexes of neighbors
if f(pj) > f(pg),
then g = j, // best neighbor performance so far
end if
end for
vi(t+1) = vi(t) + ϕ1(pi − xi(t)) + ϕ2(pg − xi(t))
vi ∈ [−vmax,vmax]
xi(t+1) = xi(t) + vi(t+1)
end for
t ← t + 1
end while
end procedure
Copyright© Leandro Nunes de Castro 243](https://image.slidesharecdn.com/computacaonaturalfull-120823094923-phpapp02/75/2012-Computacao-Natural-Slides-do-Curso-243-2048.jpg)









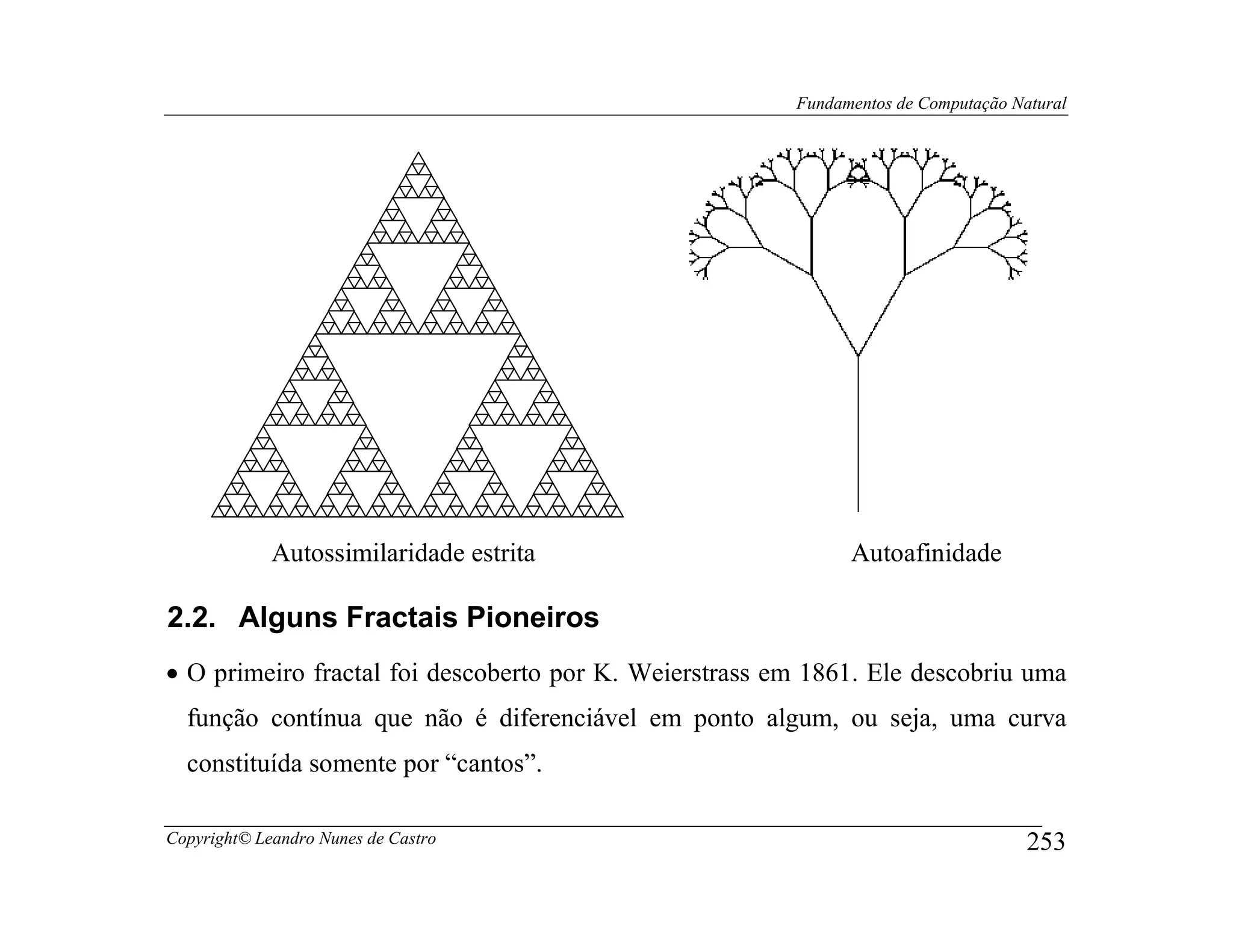




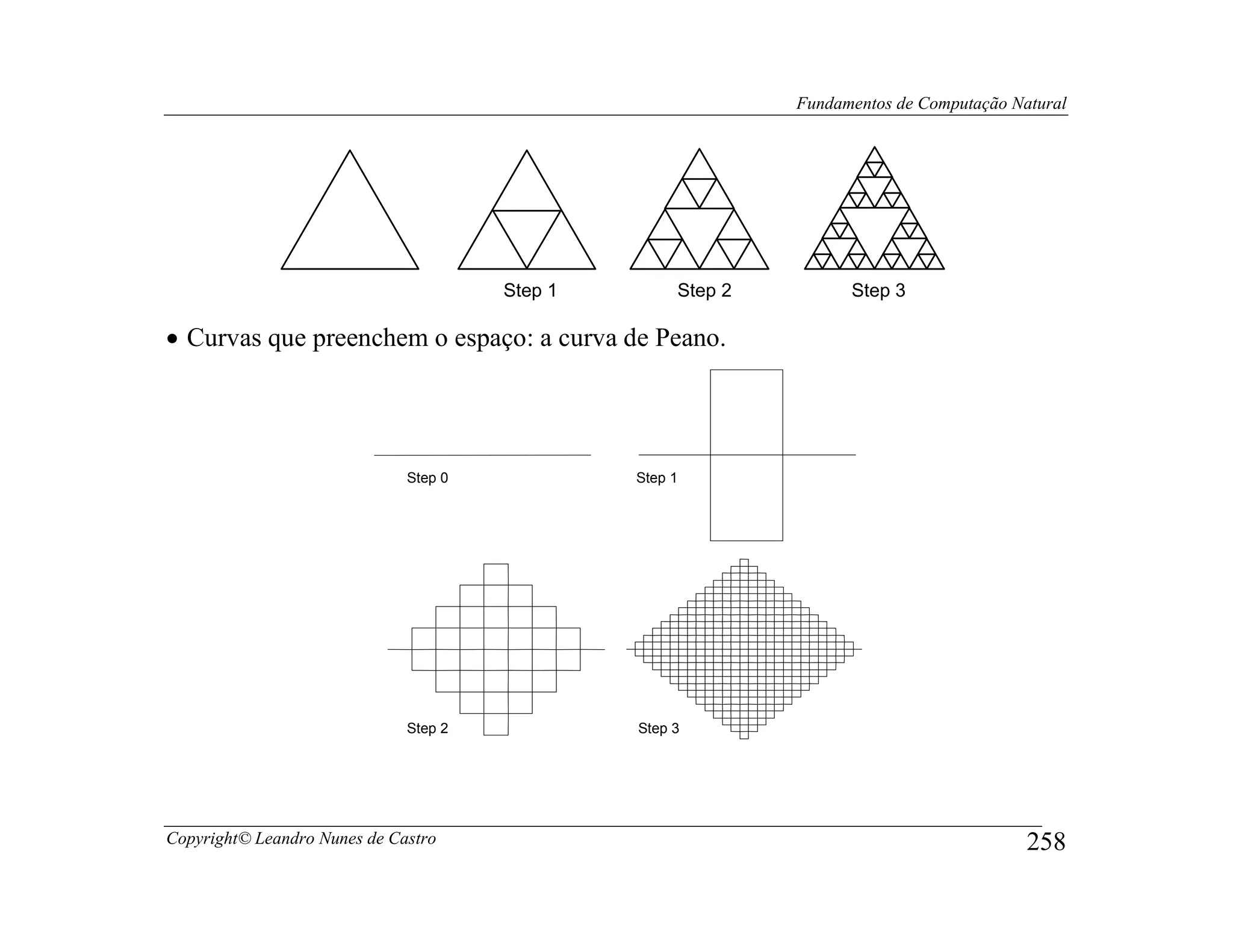





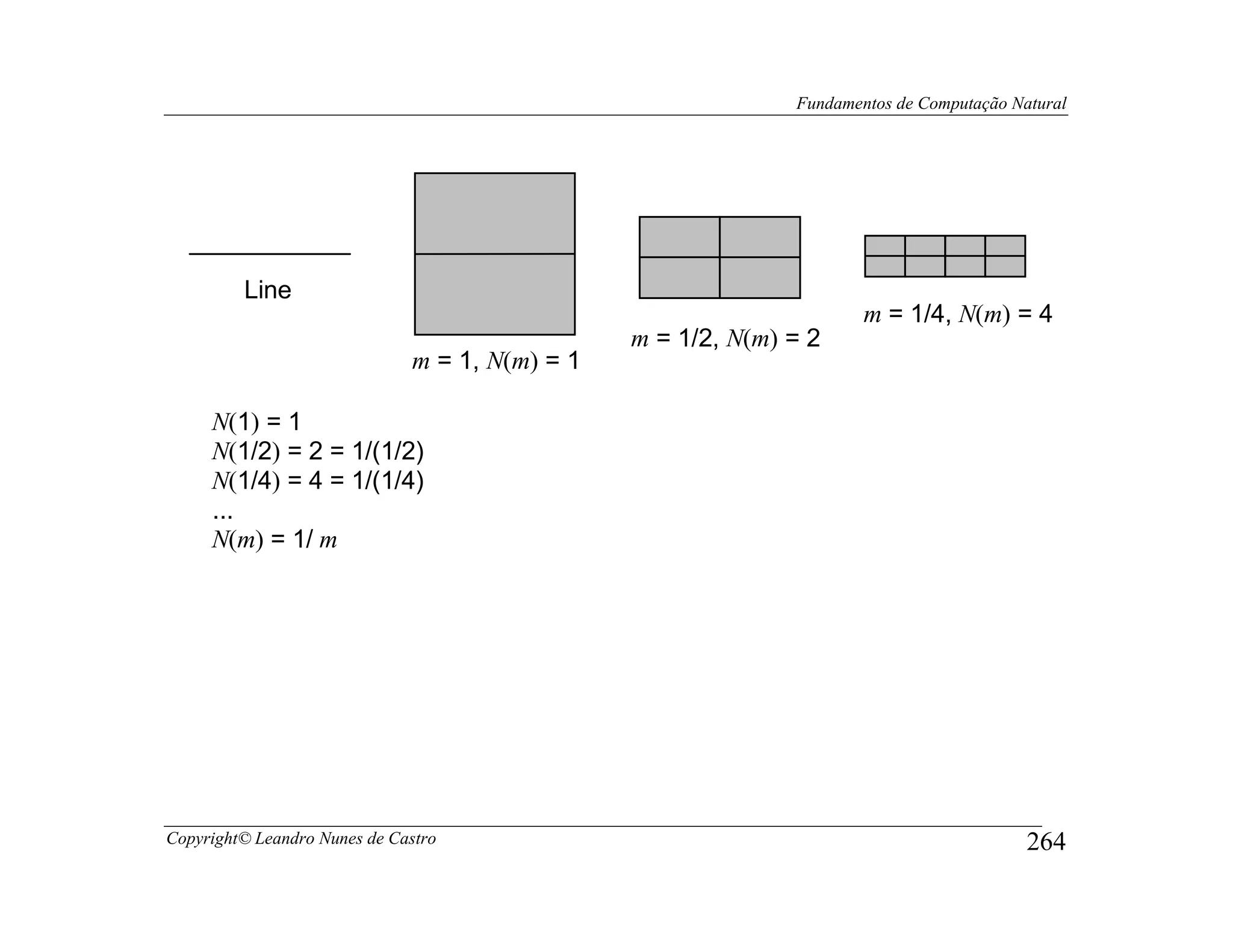















![Fundamentos de Computação Natural
4.4. Modelos de Arquiteturas de Plantas
• Em 1968, Lindenmayer estendeu os sistemas-L incluindo os colchetes {[,]} no
alfabeto dos sistemas-L, criando os bracketed L-systems.
• A motivação foi a de descrever formalmente estruturas ramificadas observadas em
plantas, algas, árvores, etc.
• Os dois novos símbolos ‘[’ e ‘]’ são interpretados pela tartaruga como a seguir:
[ Save the current state (x,y,α) of the turtle for later use onto a stack of saved
states.
] Remove the last saved state from the stack and use it to restore the turtle’s last
state. No line is drawn, although in general the position of the turtle changes.
• Exemplo: V = {F,G,[,],+,−}, axioma ω = F, δ = 45o, produções:
p1: F → G[−F]G[+F]F
p2: G → GG
p3: [ → [
Copyright© Leandro Nunes de Castro 280](https://image.slidesharecdn.com/computacaonaturalfull-120823094923-phpapp02/75/2012-Computacao-Natural-Slides-do-Curso-280-2048.jpg)
![Fundamentos de Computação Natural
p4: ] → ]
Iteration Word
0
F
1
G[−F]G[+F]F
2
GG[−G[−F]G[+F]F]GG[+G[−F]G[+F]F] G[−F]G[+F]F
• F: seta tracejada; G: seta sólida.
p2
p1
Copyright© Leandro Nunes de Castro 281](https://image.slidesharecdn.com/computacaonaturalfull-120823094923-phpapp02/75/2012-Computacao-Natural-Slides-do-Curso-281-2048.jpg)
![Fundamentos de Computação Natural
procedure [word] = DOL_turtle(max_it,ω,P,d,δ)
word ← ω
t ← 1
while t < max_it do,
word ← rewrite(word,P)
t ← t + 1
end while
turtle(word,d,δ);
end procedure
Copyright© Leandro Nunes de Castro 282](https://image.slidesharecdn.com/computacaonaturalfull-120823094923-phpapp02/75/2012-Computacao-Natural-Slides-do-Curso-282-2048.jpg)
![Fundamentos de Computação Natural
• Exemplos de plantas geradas com sistemas L.
t = 8, δ = 22.5o t = 5, δ = 22.5o
ω: G ω: G
G → F+[[G]−G]−F[−FG]+G G → FG[−F[G]−G][G+G][+F[G]+G]
F → FF F → FF
Copyright© Leandro Nunes de Castro 283](https://image.slidesharecdn.com/computacaonaturalfull-120823094923-phpapp02/75/2012-Computacao-Natural-Slides-do-Curso-283-2048.jpg)




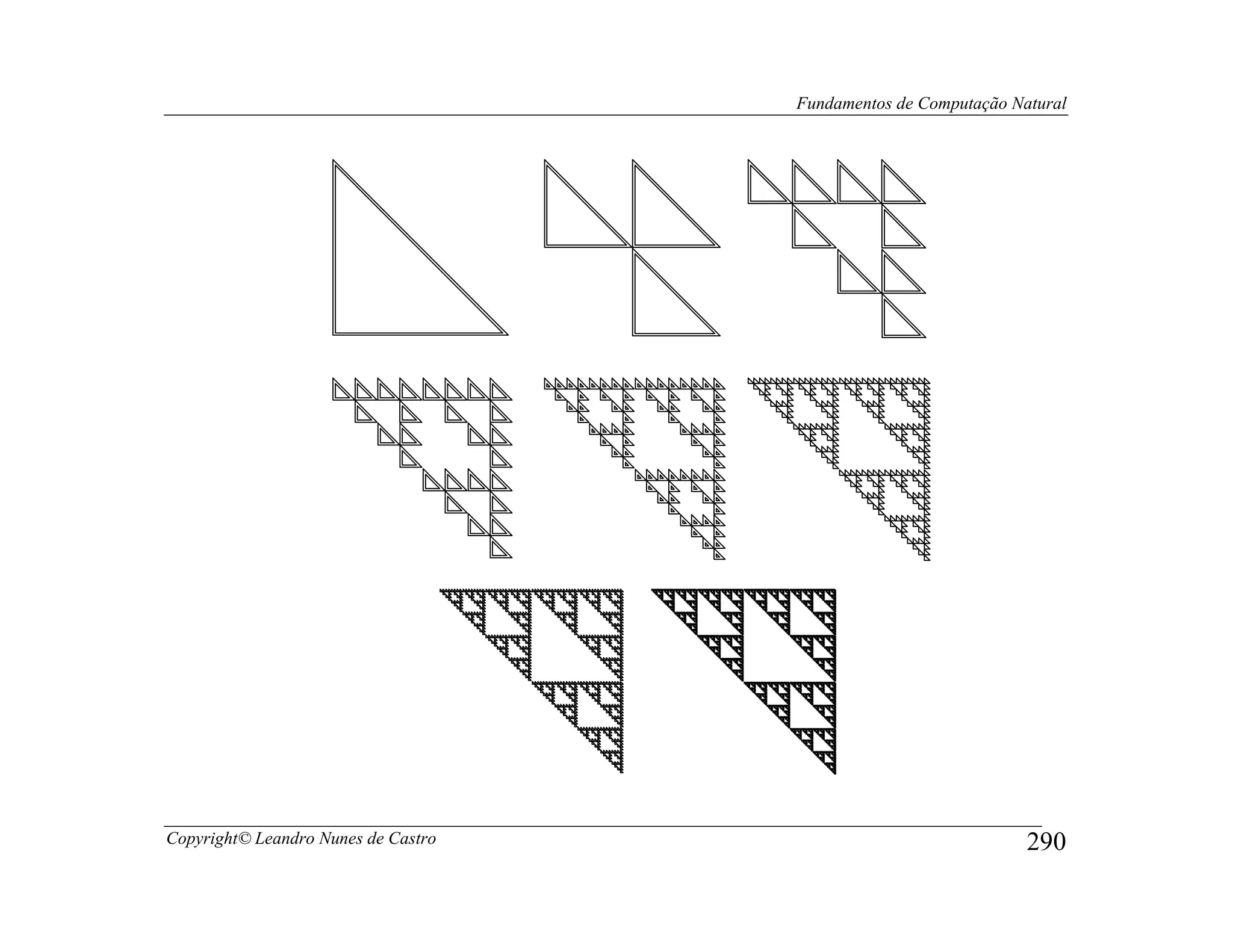
![Fundamentos de Computação Natural
Sistema aleatório de funções iterativas (random iterated function system – RIFS).
• Seja {X; w1, w2,…, wN} um IFS onde uma probabilidade pi > 0 é atribuída a cada
mapeamento wi, i = 1,…,N, ∑i pi = 1.
• Escolha x0 ∈ X e depois escolha recursivamente e independentemente
xn ∈ {w1(xn−1), w2(xn−1),…, wN(xn−1)}, ∀n
onde a probabilidade de um evento xn = wi(xn−1) ocorrer é pi.
• Portanto, construa uma sequência {xn : n = 0,1,2,…} ⊂ X.
procedure [] = RIFS(max_it,x0,W,p)
x ← x0;
t ← 1
while t < max_it do,
j ← select(p) //select a mapping j with probability pj
x ← wj(x) //apply mapping j to x
draw(x) //plot point x on the screen
t ← t + 1
end while
end procedure
Copyright© Leandro Nunes de Castro 291](https://image.slidesharecdn.com/computacaonaturalfull-120823094923-phpapp02/75/2012-Computacao-Natural-Slides-do-Curso-291-2048.jpg)
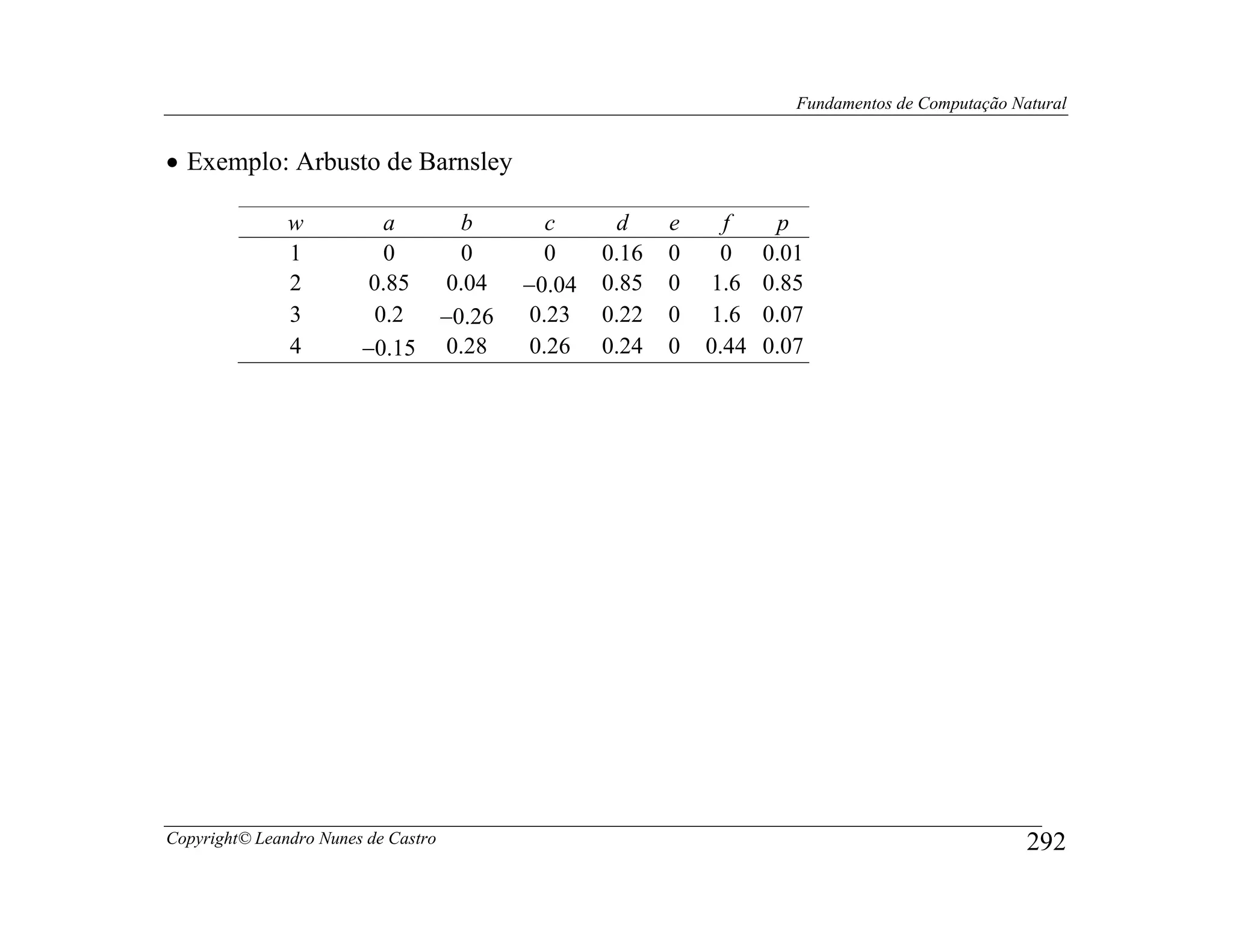






![Fundamentos de Computação Natural
procedure [] = DLA(seed)
C ← generate_C //generate Grid
Cr ← select_region(seed) //region around seed
p ← new_particle(Cr) //new particle within Cr
cs ← 1 //cluster size
while not_stopping_criterion do,
p ← move_particle //moving particle
if p meets cluster,
then attach p to cluster
cs ← cs + 1
p ← new_particle(Cr)
else
if p leaves Cr
p ← new_particle(Cr)
end if
end if
end while
end procedure
Copyright© Leandro Nunes de Castro 299](https://image.slidesharecdn.com/computacaonaturalfull-120823094923-phpapp02/75/2012-Computacao-Natural-Slides-do-Curso-299-2048.jpg)
![Fundamentos de Computação Natural
• Em uma dimensão o movimento Browniano é caracterizado por um processo
aleatório X(t), que corresponde a uma função X de uma variável real t (tempo),
cujos valores são variáveis aleatórias X(t1), X(t2), … , onde o incremento X(t2) −
X(t1) possui uma distribuição Gaussiana e os incrementos quadráticos médios têm
uma variância proporcional à diferença entre os tempos:
E[ | X(t2) − X(t2) |2 ] ∝ |t2 − t1|.
• Os incrementos de X são estatisticamente autossimilares no sentido que:
1
X(t0 + t) − X(t0) e ( X (t0 + rt ) − X (t0 )) ,
r
possuem as mesmas funções de distribuição conjuntas para quaisquer t0 e r > 0.
• Assumindo, por exemplo, t0 = 0 e X(t0) = 0, ambas as funções aleatórias
1
X(t) e ( X (rt ) ) são estatisticamente indistinguíveis; a segunda sendo uma
r
versão apropriadamente reescalonada da primeira.
Copyright© Leandro Nunes de Castro 300](https://image.slidesharecdn.com/computacaonaturalfull-120823094923-phpapp02/75/2012-Computacao-Natural-Slides-do-Curso-300-2048.jpg)
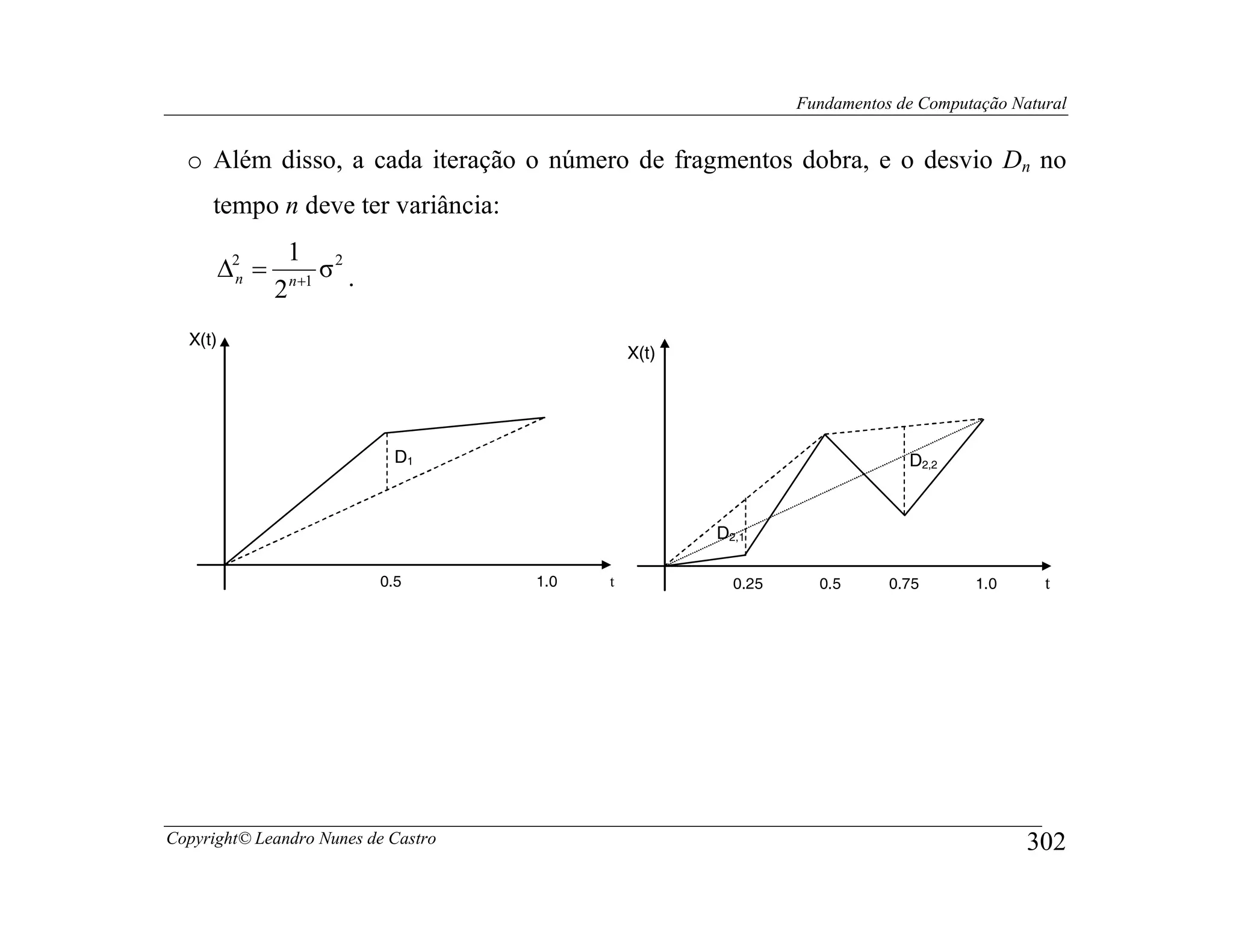
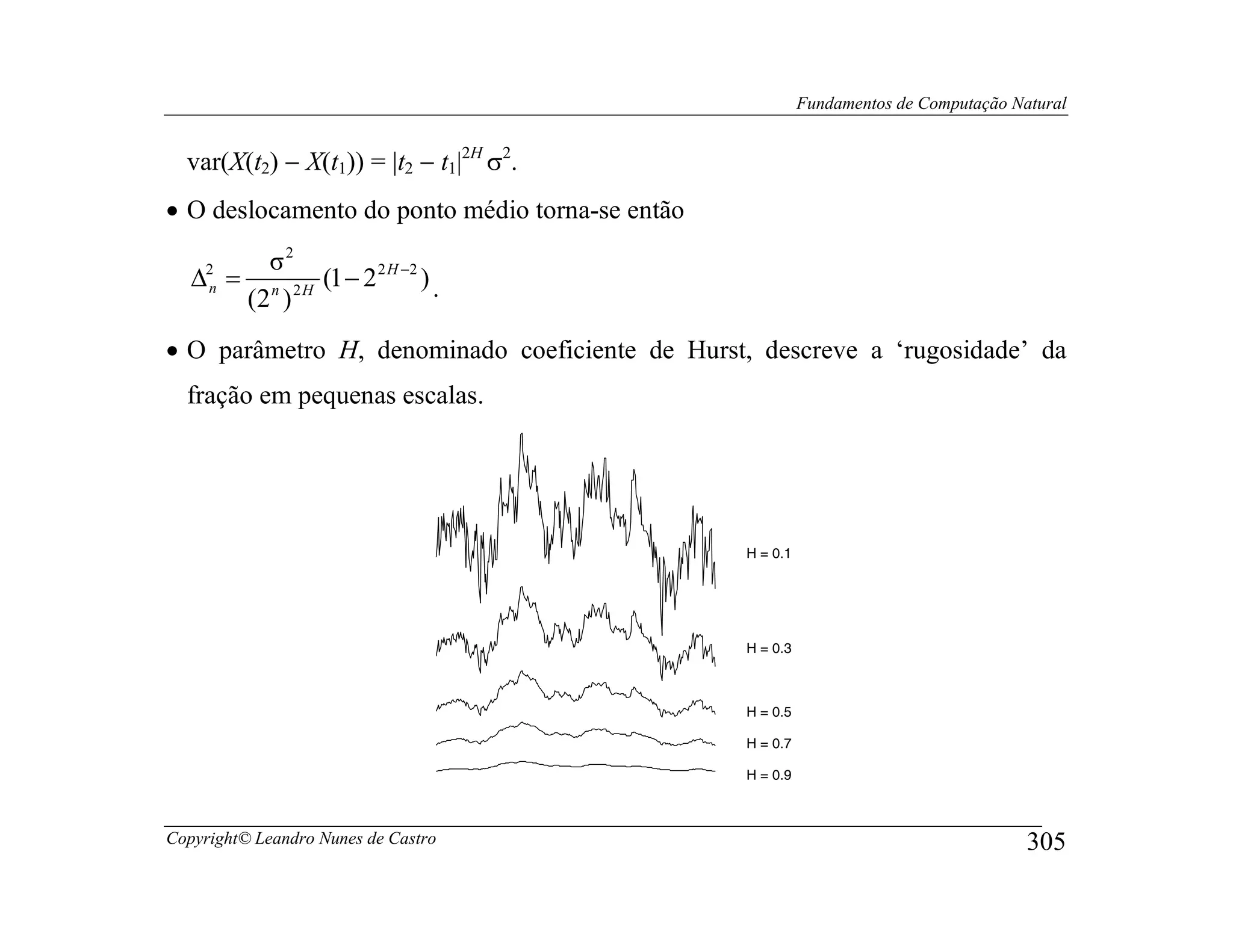
![Fundamentos de Computação Natural
• Um método popular para gerar movimento Browniano é conhecido como
algoritmo recursivo da subdivisão (recursive subdivision algorithm), também
conhecido como algoritmo do deslocamento aleatório do ponto médio (random
midpoint displacement algorithm - RMD).
• O RMD opera como a seguir:
o Se o processo X(t) deve ser computado para o tempo t ∈ [0, 1], então comece
definindo X(0) = 0 e escolhendo X(1) como uma amostra de um valor Gaussiano
de média 0 e variância σ2.
o No primeiro passo, o ponto médio entre t = 0 e t = 1 é dado pela média entre
X(0) e X(1), mais um desvio D1 de média zero e variância ∆1 :
2
X(½) − X(0) = ½(X(1) − X(0)) + D1.
o Como uma amostra de uma variável aleatória Gaussiana possui média 0 e
variância σ2, é esperado que:
var(X(t2) − X(t1)) = |t2 − t1|σ2.
Copyright© Leandro Nunes de Castro 301](https://image.slidesharecdn.com/computacaonaturalfull-120823094923-phpapp02/75/2012-Computacao-Natural-Slides-do-Curso-301-2048.jpg)
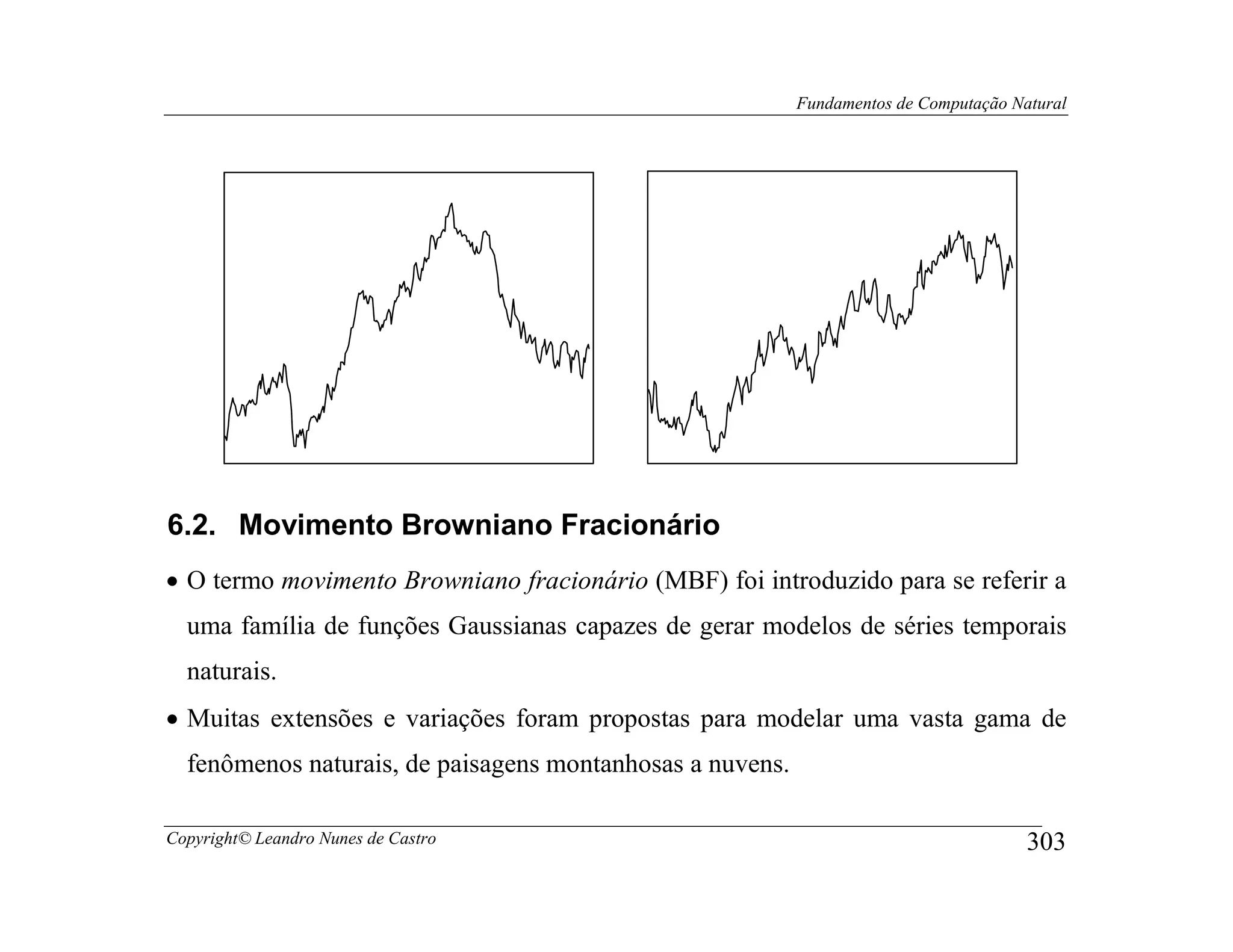









![Fundamentos de Computação Natural
• O procedimento para computar cada frame (intervalo de tempo) em uma sequência
envolve os seguintes passos:
o Geração de partículas
o Determinação dos atributos das partículas
o Morte de partículas
o Atualização das partículas
o Renderização das partículas
procedure [] = PS(max_it,d,o)
initialize X; //generate particles and assign their attributes
t ← 1
while t < max_it do,
X ← destroy(X,d) //destroy all particles older than d
X ← dynamics(X,o) //change each remaining particle
render(X) //draw (render) particles X and plot
initialize X’ //generate new particles
X ← insert(X,X’) //insert the new particles into X
t ← t + 1
end while
end procedure
Copyright© Leandro Nunes de Castro 314](https://image.slidesharecdn.com/computacaonaturalfull-120823094923-phpapp02/75/2012-Computacao-Natural-Slides-do-Curso-314-2048.jpg)























![Fundamentos de Computação Natural
3.2. Biomorphs (Bioformas)
• Com um programa chamado Blind Watchmaker, R. Dawkins (1986) propôs um
algoritmo evolutivo para gerar figuras compostas por pontos, linhas e outras
primitivas básicas.
• Os organismos artificiais criados com o blind watchmaker foram denominados de
bioformas (biomorphs).
procedure [] = evolution()
initialize; t ← 1
while not_stopping_criterion do,
reproduction //insert one mutation in each offspring
development //draw the biomorph
selection //the user chooses the new parent
t ← t + 1
end while
end procedure
Copyright© Leandro Nunes de Castro 338](https://image.slidesharecdn.com/computacaonaturalfull-120823094923-phpapp02/75/2012-Computacao-Natural-Slides-do-Curso-338-2048.jpg)




































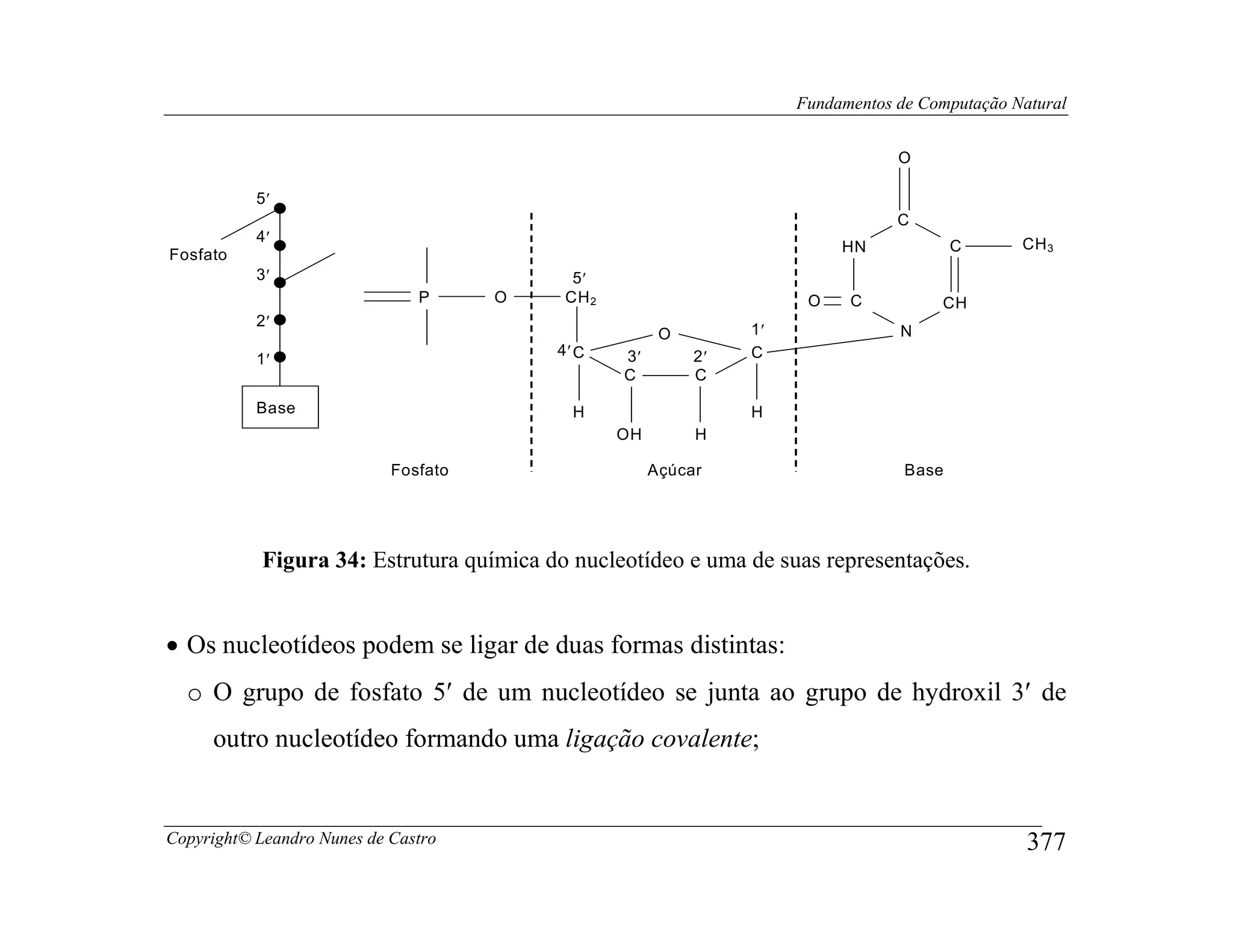


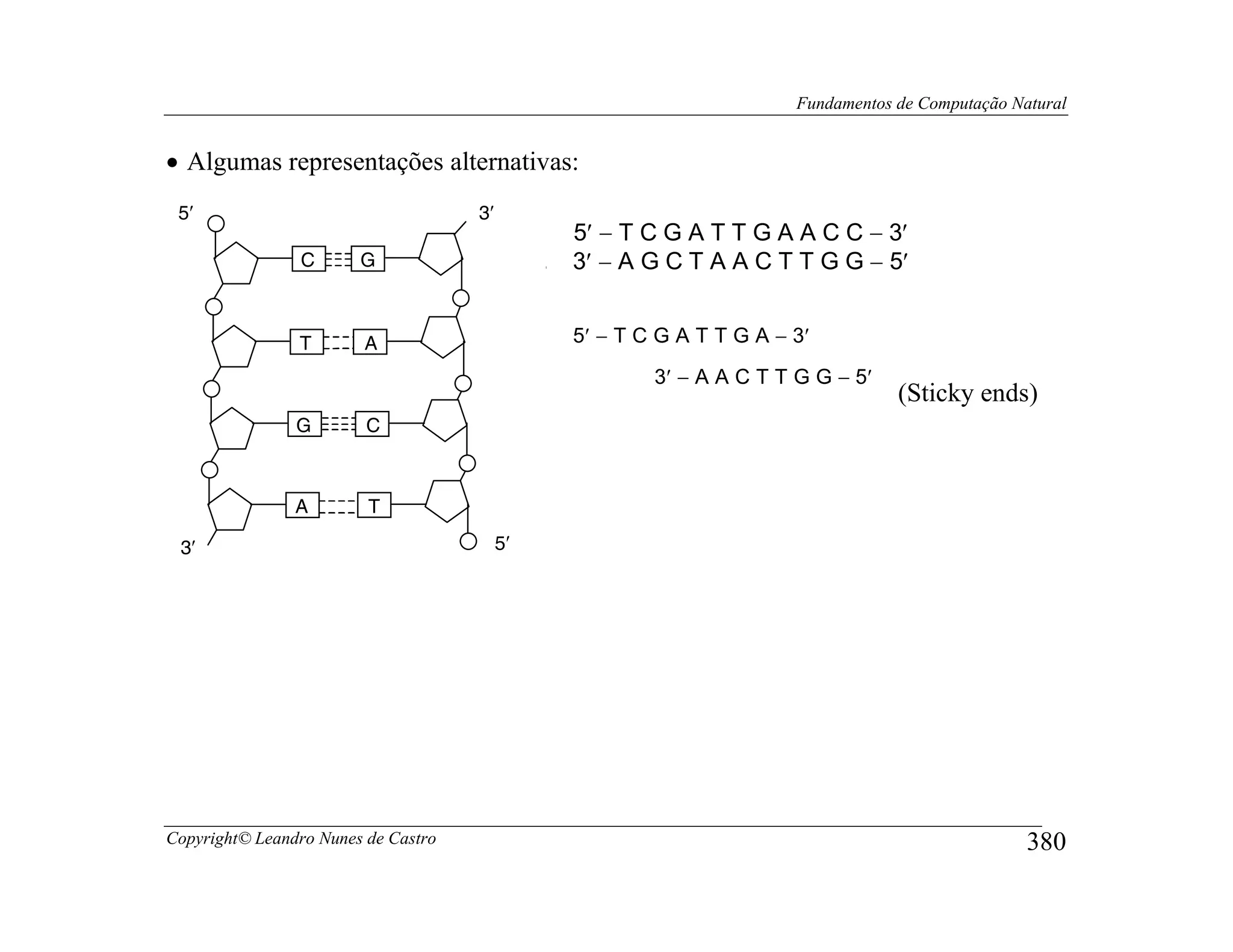

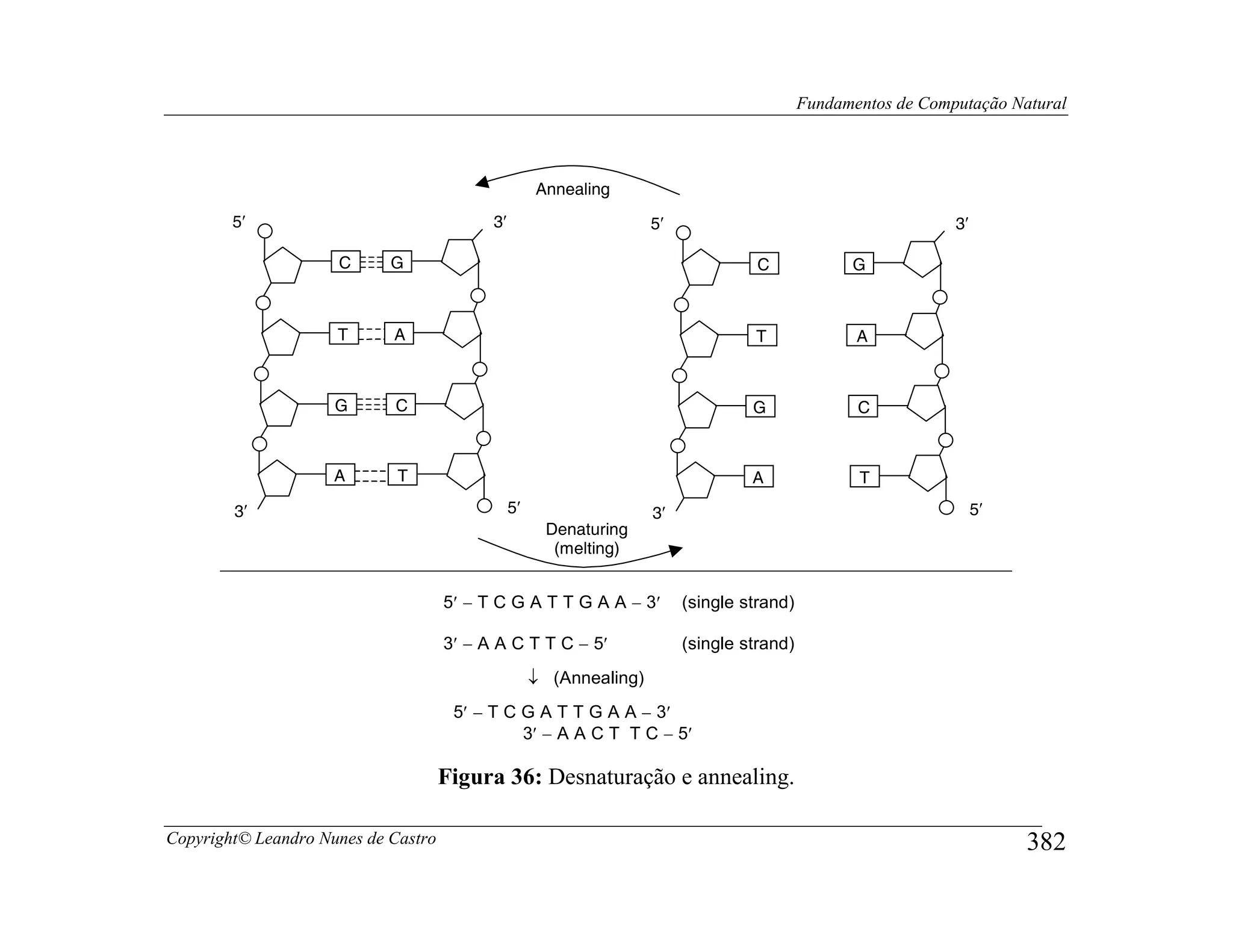


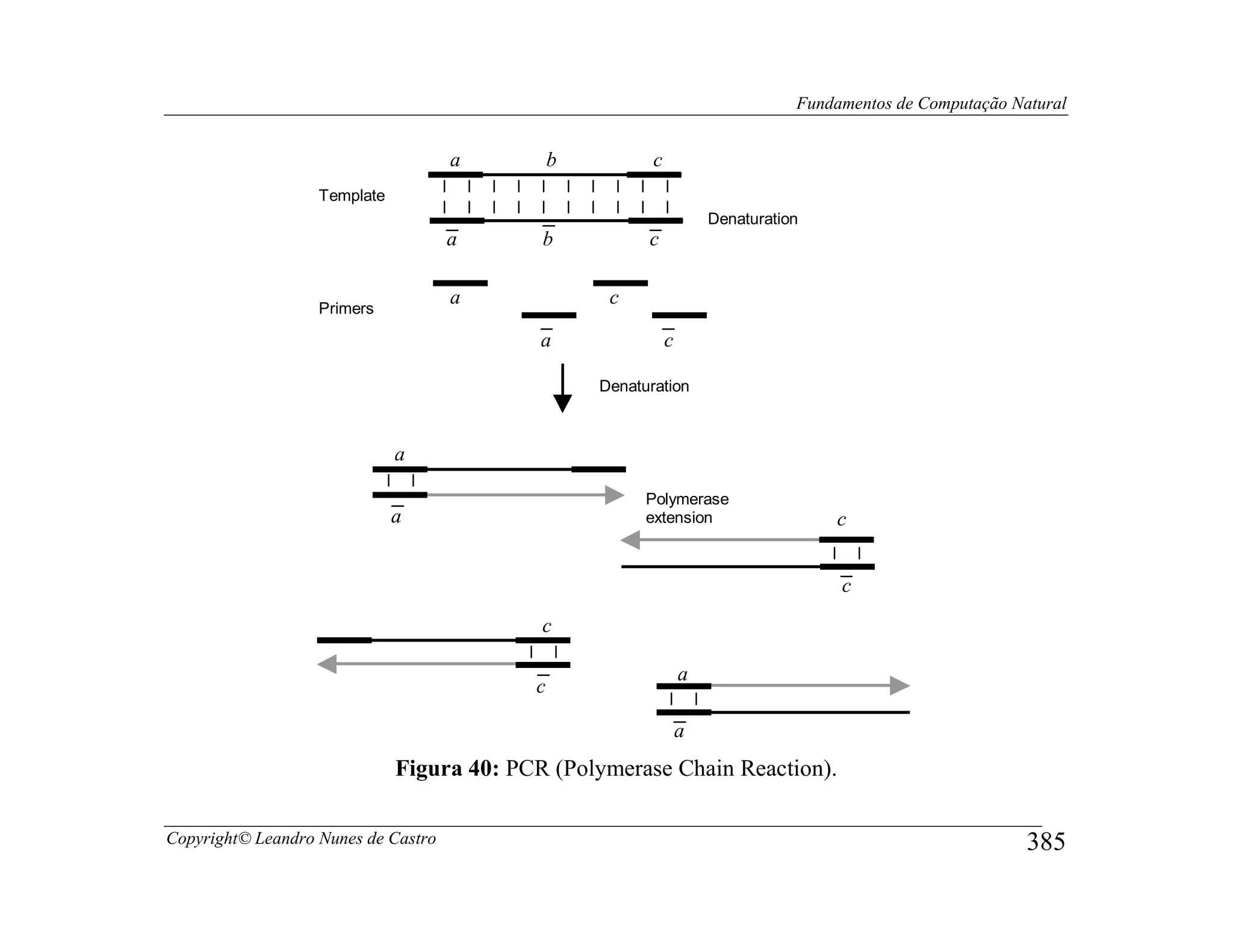
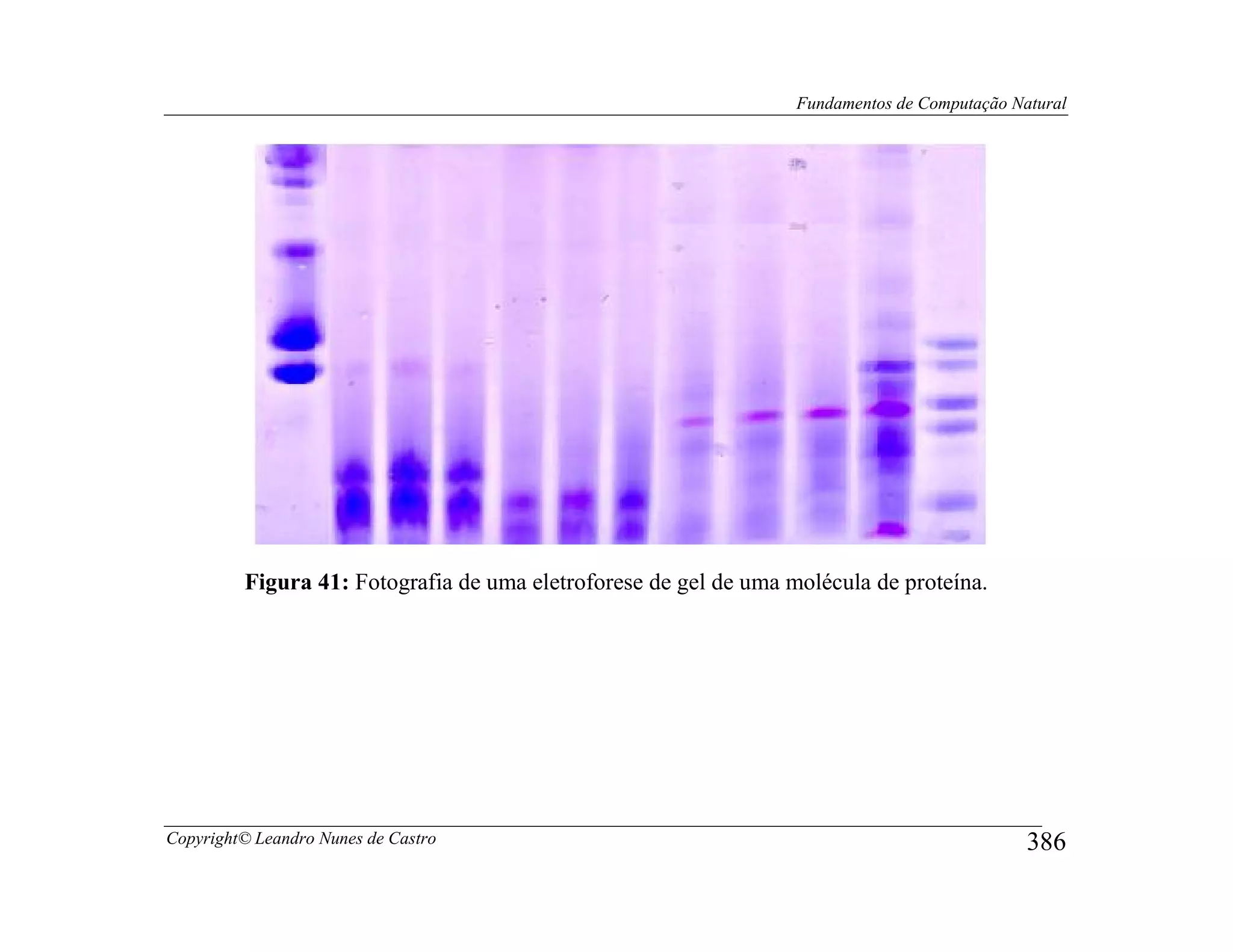




















![Fundamentos de Computação Natural
procedure [out] = extract(t,A,T,G)
t ← −(t,T)
t ← −(t,G)
t ← −(t,A)
out ← detect(t)
end procedure
o O que o programa acima faz?
Copyright© Leandro Nunes de Castro 407](https://image.slidesharecdn.com/computacaonaturalfull-120823094923-phpapp02/75/2012-Computacao-Natural-Slides-do-Curso-407-2048.jpg)
![Fundamentos de Computação Natural
procedure [out] = HPP(t,vin,vout)
t ← B(t,vin)
t ← E(t,vout)
t ← (t,≤ 140)
for i=1 to 5 do
t ← +(t,si)
end for
out ← detect(t)
end procedure
• Na proposta de Lipton para o problema SAT, uma operação extract E(t,i,a) que
extrai todas as sequências de um tubo t cujo i-ésimo bit é igual a a, foi definida:
E(t,i,a) = +(t,eia),
E−(t,i,a) = −(t,eia),
onde E−(t,i,a) extrai todas as sequências no tubo t cujo i-ésimo bit é complementar
a a.
Copyright© Leandro Nunes de Castro 408](https://image.slidesharecdn.com/computacaonaturalfull-120823094923-phpapp02/75/2012-Computacao-Natural-Slides-do-Curso-408-2048.jpg)
![Fundamentos de Computação Natural
procedure [out] = SAT(t)
t1 ← +(t,e11)
t1’ ← −(t,e11)
t2 ← +(t1’,e21)
t3 ← merge(t1,t2)
t4 ← +(t3,e10)
t4’ ← −(t3,e10)
t5 ← +(t4’,e20)
t6 ← merge(t4,t5)
out ← detect(t6)
end procedure
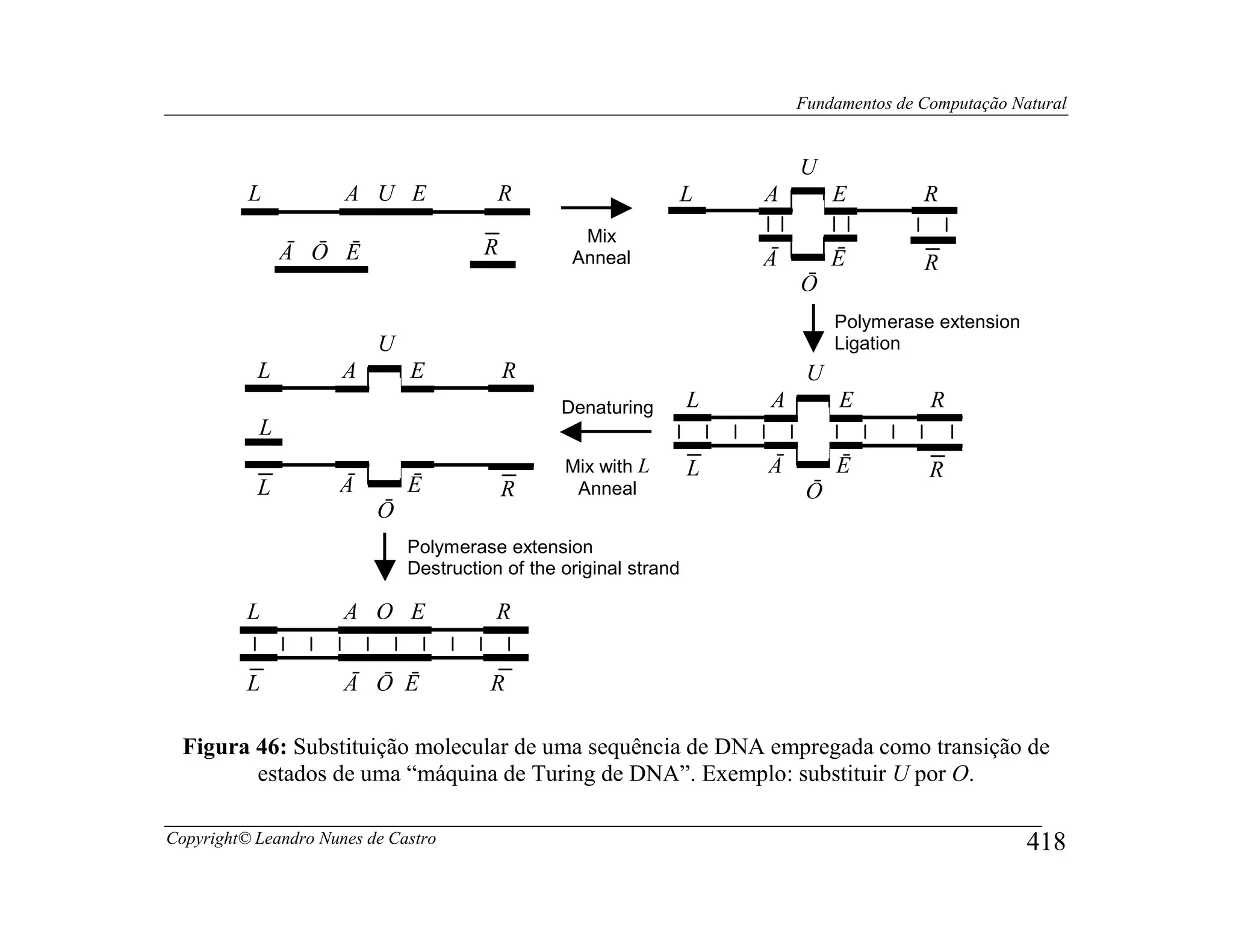
A Linguagem Pascal-DNA
• Com o objetivo de fornecer um modelo em alto nível para a computação
molecular, foi introduzida uma outra linguagem de programação combinando
elementos de Pascal com operadores de manipulação de DNA.
• Nesta linguagem, denominada de DNA Pascal, tubos de ensaio com moléculas de
DNA foram mapeados em variáveis contendo palavras do alfabeto {0,1}.
Copyright© Leandro Nunes de Castro 409](https://image.slidesharecdn.com/computacaonaturalfull-120823094923-phpapp02/75/2012-Computacao-Natural-Slides-do-Curso-409-2048.jpg)





























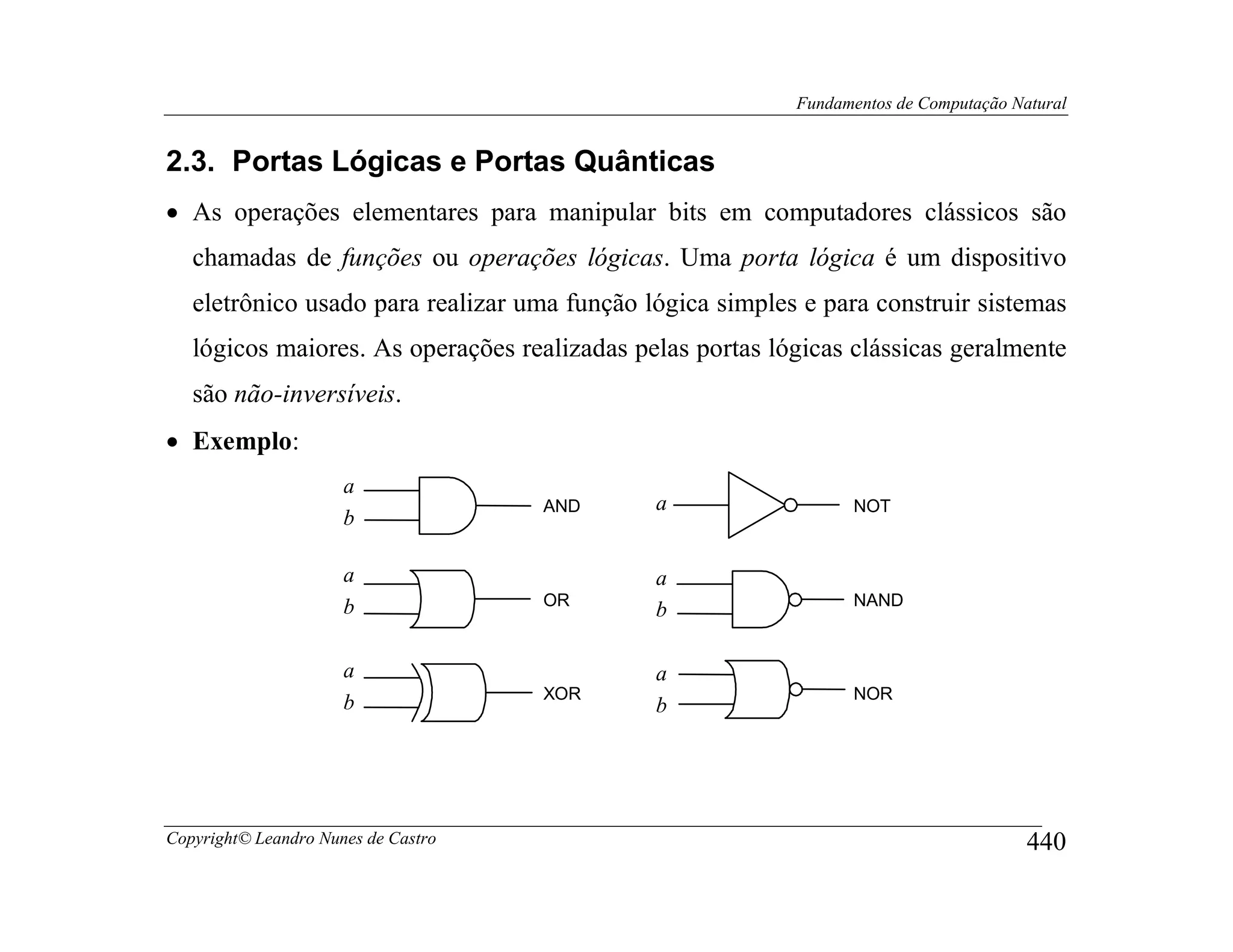













![Fundamentos de Computação Natural
• Alice aplica agora o passo de decodificação da codificação densa – uma porta
CNOT seguida de uma porta Hadamard – ao qubit desconhecido e a seu membro
do par emaranhado, o que corresponde a transformação (H⊗I⊗I)⋅(CNOT⊗I):
(H⊗I⊗I)(CNOT⊗I)(|x0〉|x〉) =
[
(H ⊗ I ⊗ I) 1 2 (c1 | 000〉 + c1 | 011〉 + c 2 | 110〉 + c 2 | 101〉 ) = ]
(H ⊗ I ⊗ I )[
1 ]
2 (c1 | 0〉 (| 00〉+ | 11〉 ) + c 2 | 1〉 (| 10〉+ | 01〉 ) ) =
1 2[c1 (| 0〉+ | 1〉 )(| 00〉+ | 11〉 ) + c 2 (| 0〉− | 1〉 )(| 10〉+ | 01〉 )] =
(23)
1 2 [| 00〉 (c1 | 0〉 + c 2 | 1〉 )+ | 01〉 (c1 | 1〉 + c 2 | 0〉 ) +
+ | 10〉 (c1 | 0〉 − c 2 | 1〉 )+ | 11〉 (c1 | 1〉 − c 2 | 0〉 )] .
• Em seguida Alice mede seus dois qubits, promovendo um colapso do estado em
uma das quatro possibilidades {00,01,10,11}.
Copyright© Leandro Nunes de Castro 454](https://image.slidesharecdn.com/computacaonaturalfull-120823094923-phpapp02/75/2012-Computacao-Natural-Slides-do-Curso-454-2048.jpg)

