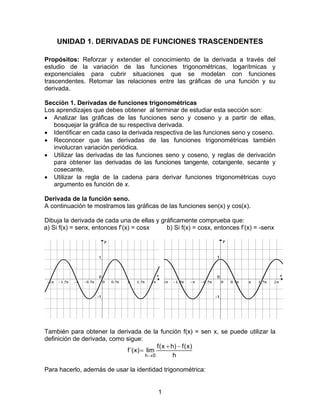
1. UNIDAD 1. DERIVADAS DE FUNCIONES TRASCENDENTES
Propósitos: Reforzar y extender el conocimiento de la derivada a través del
estudio de la variación de las funciones trigonométricas, logarítmicas y
exponenciales para cubrir situaciones que se modelan con funciones
trascendentes. Retomar las relaciones entre las gráficas de una función y su
derivada.
Sección 1. Derivadas de funciones trigonométricas
Los aprendizajes que debes obtener al terminar de estudiar esta sección son:
• Analizar las gráficas de las funciones seno y coseno y a partir de ellas,
bosquejar la gráfica de su respectiva derivada.
• Identificar en cada caso la derivada respectiva de las funciones seno y coseno.
• Reconocer que las derivadas de las funciones trigonométricas también
involucran variación periódica.
• Utilizar las derivadas de las funciones seno y coseno, y reglas de derivación
para obtener las derivadas de las funciones tangente, cotangente, secante y
cosecante.
• Utilizar la regla de la cadena para derivar funciones trigonométricas cuyo
argumento es función de x.
Derivada de la función seno.
A continuación te mostramos las gráficas de las funciones sen(x) y cos(x).
Dibuja la derivada de cada una de ellas y gráficamente comprueba que:
a) Si f(x) = senx, entonces f’(x) = cosx b) Si f(x) = cosx, entonces f’(x) = -senx
También para obtener la derivada de la función f(x) = sen x, se puede utilizar la
definición de derivada, como sigue:
f ( x + h) − f ( x )
f´( x ) = lim
h→0 h
Para hacerlo, además de usar la identidad trigonométrica:
1

2. sen(x+y) = senx cosy + seny cosx
se necesita que recuerdes los siguientes límites, para lo cual te solicitamos
completes las tablas correspondientes y, con ello, compruebes los resultados
indicados:
senx 1-cosx lim senx lim cos x
x lim lim x →0 x →0
x →0 x x →0 x
0.1
0.01
0.001
0.0001
0.00001
0.000001
0.0000001
0 1 0 0 1
Teniendo lo anterior, a continuación encontraremos la derivada de la función
sen(x). Sigue cada uno de los pasos:
sen(x + h) − sen x sen x cosh + senhcos x − sen x
f '(x) = lim = lim
h →0 h h→0 h
factorizando – senx, del primero y tercer términos obtenemos:
− sen x( − cosh+ 1) + senhcos x
f '(x) = lim
h→0 h
luego,
− sen x(1 − cosh) senhcos x
f '(x) = lim + lim
h →0 h h →0 h
1 − cosh senh
f '(x) = −senx lim + cos x lim = cos x
h→0 h h →0 h
Resumiendo:
d(sen x )
= cos x
dx
De lo anterior y por la regla de la cadena, podemos concluir que si u es una
función diferenciable1, entonces:
dsenu du
= cosu
dx dx
1
Una función es diferenciable en un intervalo dado abierto si f’(x) existe para toda x en
ese intervalo.
2

3. Ahora estamos en condiciones de derivar funciones que contengan a la función
seno.
Ejemplo 1. Encuentra la derivada de g(x) = –5sen (–2x).
d( −5 sen( −2x)) dsen( −2x) d( −2x)
Solución. = −5 = −5cos( −2x) = 10cos( −2x) .
dx dx dx
Ejemplo 2. Encuentra la ecuación de la recta tangente a la curva f(x) = sen 2x,
π
cuando x = .
2
Solución. Para determinar la ecuación de la recta tangente, necesitamos su
pendiente y el punto de tangencia. Su pendiente la encontraremos al calcular:
π
f´( ) , lo cual haremos a continuación:
2
dsen(2x) d(2x)
f '(x) = = cos(2x) = 2cos(2x) =2cos2x
dx dx
Habiendo encontrado la fórmula2 (f’(x) =2cos2x) podemos determinar la pendiente
de la recta tangente a la gráfica de la función f(x) = sen2x en cada punto de su
gráfica, pasamos a encontrar en particular la pendiente de la recta tangente en el
π π
punto ( ,f( ))
2 2
π π
f´( ) = 2cos (2 ) = 2cosπ =2(–1) = –2
2 2
π
La ordenada, f( ), del punto de tangencia es igual a:
2
π π
f( ) = sen(2 ) = sen π = 0 .
2 2
Así pues, la ecuación de la recta tangente a la gráfica de la función f(x) = sen 2x,
π π
en el punto ( ,0) es: y - 0 = –2(x – ) , o bien
2 2
2x + y – π = 0.
Ejemplo 3. Encuentra la derivada de la función h(x) = sen x
d u 1 du
Solución. Recordando que: = , obtenemos:
dx 2 u dx
d sen x 1 dsen x cos x
h'(x) = = = .
dx 2 sen x dx 2 sen x
2
Cuando no se presta a confusión se acostumbra escribir cos2x en lugar de cos(2x).
3

4. 7
Ejemplo 4. Encuentra la derivada de f(x) = sen(6x 2 )
3
d ⎛7 2 ⎞ 7 d 7 d
Solución. f '(x) = ⎜ 3 sen(6x ) ⎟ = 3 dx sen(6x ) = 3 cos(6x ) dx 6x =
2 2 2
dx ⎝ ⎠
7
f '(x) = cos(6x 2 )(12x) = 28x cos(6x 2 ) .
3
Ejemplo 5. Encuentra la derivada de s(t) = sen3t
d d
Solución. s'(t) = sen3 t = 3sen2 t sen t = 3sen2 t cos t .
dt dt
Ejemplo 6. Calcula la derivada de m(t) = sen t3
d d
Solución. m'(t) = sen t 3 = cos t 3 t 3 = 3t 2 cos t 3 .
dt dt
Ejemplo 7. Calcula la derivada de: k(x) = x2 sen(4x3)
d 2 d d
Solución. k '(x) = x sen(4x3 ) = x 2 sen(4x 3 ) + sen(4x3 ) x 2 =
dx dx dx
k '(x) = x cos(4x )(12x ) + 2x sen(4x ) = 12x cos(4x 3 ) + 2x sen(4x 3 )
2 3 2 3 4
Resuelve los siguientes ejercicios. Al terminarlos, comprueba tus resultados al
final de la guía.
Ejercicios 1
Calcula la derivada de cada una de las siguientes funciones:
sen x 1
1. v( x ) = 2. y = 2 − 4 sen 3 x 4 3. t( x ) = −7 sen
x x
1
4. h(t) = 2
5. s(w) = (2w − 1)3 sen w 6. f(x) = sen2x2
sen t
Derivada de la función coseno.
Para encontrar la derivada de la función f(x) = cosx, hacemos uso de la siguiente
identidad trigonométrica:
sen2x + cos2x = 1
Derivándola de manera implícita obtenemos:
dsen2 x dcos2 x d1
+ =
dx dx dx
dsen x dcos x
2sen x + 2cos x =0
dx dx
4

5. dcos x
2sen x cos x + 2cos x =0
dx
dcos x
2cos x = −2sen x cos x
dx
d(cos x )
= − sen x
dx
De lo anterior y usando la regla de la cadena podemos concluir que:
dcosu dcosu du du
= = −senu
dx du dx dx
Ejemplo 8. Encuentra g´(x), si g( x ) = sen x cos x
Solución. Como es un producto de funciones, entonces:
d(cos x ) d(sen x )
g' ( x ) = (sen x ) + (cos x )
dx dx
= (sen x )(− sen x ) + (cos x )(cos x )
g´(x) = − sen2 x + cos2 x
dy
Ejemplo 9. Calcula , si y = m cos ax 2 , en donde a y m ∈
dx
Solución.
dy d dax 2
= mcosax 2 = −m senax 2 = ( −m senax 2 )(2ax) = −2amx senax 2 .
dx dx dx
− 5x 2
Ejemplo 10. Calcula la derivada de: f ( x ) =
cos 3 x
d −5x 2
(cos3x)( −10x) − ( −5x 2 )( −sen3x)(3)
Solución. f '(x) = = =
( cos3x )
2
dx cos3x
−10x cos3x − 15x 2 sen3x
f '(x) = .
cos2 3x
Ejemplo 11. Encuentra la pendiente de la recta normal a la gráfica de la función
π π
f(x) = x cosx, en el punto P( , )
3 6
Solución. Para resolver este ejemplo debes recordar que la recta normal y la
tangente tienen la propiedad de que el producto de sus pendientes es –1. Hecho
lo anterior, pasamos a determinar la fórmula de las pendientes de las rectas
tangentes a la gráfica de f(x), es decir su derivada:
5

6. d d d
f '(x) = x cos x = x cos x + cos x x = − xsenx + cos x
dx dx dx
π π
Ahora, determinaremos la pendiente de la recta tangente en el punto P( , ) , o lo
3 6
π
que es lo mismo f '( ) :
3
π π π π π
f '( ) = − sen( ) + cos( ) = − sen60º + cos 60º =
3 3 3 3 3
π π 3 1 3−π 3
f '( ) = − + =
3 3 2 2 6
Una vez encontrada la pendiente de la recta tangente, determinaremos la
pendiente de la recta normal (mN) a partir del hecho de que su producto con la
recta tangente es –1:
π
f '( )mN = −1
3
−1 −1 6
mN = = =− .
π 3−π 3 3−π 3
f '( )
3 6
Ejemplo 12. Encuentra las dimensiones del rectángulo de mayor área inscrito en
un círculo de radio 1.
2
y
α
x
Solución. Como se nos pide el rectángulo inscrito de mayor área, debemos
encontrar una fórmula del área de ese rectángulo y aplicarle tus conocimientos de
cálculo diferencial para determinar sus lados.
Sean x, y los lados del rectángulo inscrito en el círculo y α el ángulo comprendido
entre una de sus diagonales y el lado x, como se muestra en la figura.
El área del rectángulo es A =xy. Así escrita la función A depende de dos variables,
por lo que debemos encontrar una relación entre ellas que nos permita rescribir a
la función A en términos de sólo una variable.
Del triángulo formado por los dos lados del triángulo y la diagonal, tenemos que
y x π
sen α = , cos α = , en donde 0 < α < .
2 2 2
6

7. Por lo tanto
y = 2 sen α , x = 2 cos α ,
Así pues,
A = xy = (2senα)(2cosα) = 4 senα cosα.
Con lo anterior hemos logrado que la función A dependa de una variable
A(α) =4 senα cosα
Al derivarla obtenemos:
A´(α) = 4(sen α( − sen α) + cos α(cos α))
A´(α) = 4(cos 2 α − sen 2 α )
Determinemos los números críticos igualando a cero la derivada y resolviendo la
ecuación resultante:
A´(α) = 0 ⇒ 4(cos 2 α − sen 2 α ) = 0 ,
de donde
cos 2 α = sen 2 α .
Como α es un ángulo agudo, entonces senα y cosα son positivos, por lo que
senα = cosα,
π
lo cual ocurre cuando α = .
4
π
Cuando α = A´(α) es igual a cero, para saber si con este valor, el área es
4
máxima o mínima, calculemos la segunda derivada: y determinemos el signo de
π
A ''( ) .
4
A´´(α) = 4( −2 cos α sen α − 2 sen α cos α)
A´´(α ) = −16cos α sen α
2
π π π ⎛ 2⎞
A´´( ) = −16 cos sen = −16⎜ ⎟
⎜ 2 ⎟ = −8 < 0
4 4 4 ⎝ ⎠
π
Por lo anterior, el área tiene un máximo cuando α = . Los valores de los lados
4
del rectángulo inscrito en un círculo de radio 1 son:
π 2 π 2
x = cos = , y = sen = ,
4 2 4 2
es decir, se trata de un cuadrado de área:
⎛ 2 ⎞⎛ 2 ⎞
A = 4⎜ ⎟⎜ ⎟
⎜ 2 ⎟⎜ 2 ⎟ = 2 .
⎝ ⎠⎝ ⎠
7

8. Ejercicios 2
Calcula la derivada de cada una de las siguientes funciones:
sen t x
1. y = cos 4x 2. h( t ) = 3. j( x ) =
3 + 2 cos t cos x
2
1 + sen x 4π
4. k( w ) = 5 − 4 cos 2w 5. m( x ) = 6. p( t ) = − cos t sen t
cos 3 x 3
7. La sección transversal de un canal de agua tiene forma de triángulo isósceles.
Si los lados iguales miden 20 cm. Encuentra la medida del ángulo comprendido
entre los lados iguales, que de la máxima capacidad de agua que puede
contener la canal.
θ
Derivada de otras funciones trigonométricas
La derivada de las funciones tangente, cotangente, secante y cosecante, las
puedes obtener a partir de expresarlas en términos de seno o coseno, recuerda
que:
sen x cos x 1 1
tanx = cot x = sec x = csc x =
cos x sen x cos x sen x
dtan x
Ejemplo 13. Encuentra
dx
Solución.
dtan x d ⎛ sen x ⎞ cos x(cos x) − senx( −senx) cos2 x + sen2 x
= = =
dx dx ⎜ cos x ⎟
⎝ ⎠ (cos x)2 cos2 x
Usando la identidad sen 2 x + cos 2 x = 1 y que secx = 1/ cosx, obtenemos
dtan x 1
= = sec 2 x
dx cos2 x
En resumen:
dtan x
= sec 2 x
dx
De lo anterior y por la regla de la cadena, concluimos que si u es una función
diferenciable, entonces:
8

9. dtanu du
= sec 2 u
dx dx
Ejemplo 14. Calcula la derivada de la función y = tan 1 − x 3
Solución.
dy d d −3x 2
= tan 1 − x 3 = sec 2 1 − x 3 1 − x 3 = sec 2 1 − x 3 =
dx dx dx 2 1 − x3
dy −3x 2 sec 2 1 − x 3
=
dx 2 1 − x3
Ejercicios 3
d
1. Demuestra que: (cot x ) = − csc 2 x
dx
d
2. Demuestra que: (sec x ) = sec xtanx
dx
d
3. Demuestra que: (csc x ) = − csc x cot x
dx
4. Si u es una función diferenciable, usando la regla de la cadena y los resultados
de los tres ejercicios anteriores, encuentra las fórmulas para:
d d d
a) (cot u) b) (sec u) c) (csc u)
dx dx dx
5. Calcula la derivada de cada una de las funciones siguientes:
a) f(x) = sec x b) g(x) = cos (5x2 + 2)3
c) h(x) = cos x2 – cos2x d) m(t) = tan 4t2
6. Encuentra la ecuación de la recta tangente a la curva de la gráfica de la función
π
y = –3tanx cuando x = .
4
Sección 2. Derivadas de funciones exponenciales y logarítmicas.
Los aprendizajes que debes obtener al terminar de estudiar esta sección son:
• Analizar las gráficas de las funciones logarítmica y exponencial y a partir de
ellas bosqueja las gráficas de sus derivadas.
• Identificar en cada caso la derivada respectiva de las funciones logarítmica y
exponencial.
• Utilizar la regla de la cadena para derivar funciones logarítmica y
exponencial cuyo argumento es función de x.
• Aplicar las derivadas de funciones logarítmica y exponencial a problemas
diversos.
Definición. Una función exponencial es una función que tiene la forma:
f(x) = bx,
en donde la base b es una constante positiva, x ∈ R y f(x) es positiva.
9

10. A continuación trabajaremos con ejemplos de funciones exponenciales.
A continuación te presentamos las gráficas de las funciones: f(x) = 2x, f(x) = 3x,
f(x) = 4x y f(x) = 5x.
¿Cuál es la gráfica de cada función? Para contestar la pregunta debemos de
considerar el comportamiento que tiene cada una de las funciones con respecto
de las otras. Es claro que todas la funciones exponenciales deben pasar por el
punto (0,1), ¿por qué?
¿Cuál es la función que crece más rápidamente? La función f(x) = 5x, debido a que
conforme x va aumentando sus valores van siendo mayores que los de las otras
tres funciones. Así pues, la gráfica de la función que para valores mayores que
cero está por encima del resto es la de f(x) = 5x. La gráfica que está más abajo es
la de f(x) = 4x, luego f(x) = 3x y finalmente la de f(x) = 2x. Observa que no ocurre lo
mismo cuando x es negativa, a la izquierda del cero, la situación es diferente. Lo
anterior ocurre porque, por ejemplo, cuando x = -2, las funciones: f(x) = 2x,
f(x) = 3 x , f(x) = 4x y f(x) = 5x, tomarán los siguientes valores:
1 1 1 1 1
f( −2) = 2−2 = 2 = = 0.25 , f( −2) = 3−2 = 2 = = 0.13, f( −2) = 4−2 = = 0.0625 ,
2 4 3 9 16
1 1
f( −2) = 5−2 = 2 = = 0.04 , respectivamente. Para valores menores que cero,
5 25
conforme x va disminuyendo, las funciones exponenciales cuya base es de un
valor mayor, disminuyen más rápidamente con respecto a las que tienen una base
menor.
−
3
Debe recordarse que así como 0.3 significa 0.3333333... (infinidad de números tres),
0.1 se debe entender como 0.11111111... (infinidad de números unos)
10

11. Te aconsejamos que recuerdes las siguientes leyes de los exponentes:
1
( )
m
■ anam= an+m ■ an = anm ■ a−n = n , a ≠ 0
a
n
( )
n
a n
■ m = an − m , a ≠ 0 ■ a m = m an = m a ■ a0 = 1, a ≠ 0.
a
La función y = ex.
Bien lo dicen Kasner y Newman 4“Un universo donde faltaran π y e (...) no sería
inconcebible. Difícilmente uno podría imaginarse que el Sol dejaría de salir o que
las mareas cesaran por la falta de π y e. Pero sin estos artificios matemáticos, lo
que sabemos del Sol y las mareas, e incluso nuestra capacidad para describir
todos los fenómenos naturales, físicos, biológicos, químicos o estadísticos,
quedarían reducidos a dimensiones primitivas.”
De las funciones exponenciales la más importante, sin duda, se da cuando b = e.
El número e se ha encontrado como una constante que aparece en la naturaleza
en diversos problemas de crecimiento exponencial. A dicho número se le asignó la
letra e en honor al matemático Leonardo Euler, quien calculó el número con 23
decimales correctos (en una época en la que, obviamente, no existían las
calculadoras) obteniendo el siguiente resultado:
e = 2.71828182845904523536028...
El número e se encuentra cuando se determina el siguiente límite:
n
⎛ 1⎞
e = lim ⎜ 1 + ⎟
n →∞
⎝ n⎠
Con el fin de que encuentres una aproximación del número e, realiza la siguiente
tabulación.
n
⎛ 1⎞
n ⎜1+ n ⎟
⎝ ⎠
1
10
102
103
104
105
106
107
108
109
4
Kasner y Newman, Matemáticas e Imaginación. Ed. CECSA, México 1972.
11

12. La función logaritmo como inversa de la exponencial.
Ahora trazaremos una gráfica simétrica a la función f(x) = ex con respecto a la
recta y = x. Para hacerlo utilizaremos las gráficas de f(x) = x, y de f(x) = ex, así
como la tabulación de esta última:
x -3 -2 -1 0 1 2 3
x
f(x) = e 1 1 1 1 e e 2
e3
e3 e2 e1
El punto simétrico al punto (0,1) es el punto (1,0); el de (1,e) es (e,1); el de (-1,1/e)
es (1/e,-1); el de (-2,1/e2) es (1/e2,-2); y el de (-3,1/e3) es (1/e3,-3). ¿Cuál es el
punto simétrico de (3,e3)?
Basándonos en los puntos que hemos encontrado hemos trazado la gráfica. La
función correspondiente a la gráfica encontrada es f(x) = ln(x).
De la gráfica de ln(x) podemos determinar lo siguiente:
1) ln(1) = 0.
+
2) El dominio de ln(x) es R y su rango R .
3) ln(e) = 1.
4) eln(1) = 1
En la gráfica que se presenta a continuación hemos colocado inicialmente el valor
de eu, luego se ha encontrado el valor de ln(eu), utilizando la gráfica de logaritmo
natural. También, utilizando la gráfica de y = x, hemos encontrado ese mismo valor
sobre el eje Y. De la gráfica de ex hemos proyectado el valor de u, porque dicho
valor tomado a partir del eje X sobre la gráfica de ex nos proporciona eu sobre el
eje Y. La propiedad mostrada en la gráfica se puede sintetizar como sigue:
12

13. 5) lneu= u
eu
ln(eu), u
u eu
Otra propiedad, que te dejamos como ejercicio de tarea para mostrarla
gráficamente, es:
6) elnu = u.
Cuando trabajamos con una función f, denotamos por f(2) al valor que la función le
asigna al número 2. Si alguna persona escribe en lugar de f(2) f2, consideramos
incorrecta dicha escritura. Por lo anterior es importante aclarar en el caso de las
funciones logarítmicas, al igual que en las trigonométricas, es válido escribir ln(2) o
bien ln2. Nosotros a lo largo del texto las utilizaremos indistintamente. También es
necesario recordar que (lnx)p se puede escribir como lnpx, pero no como lnxp.
Es importante recordar que otra forma, muy práctica y que fue lo que motivo su
uso, es que si
23 = 8,
entonces podemos afirmar que
log28 = 3.
En general, si
bn = x,
entonces
logbx = n,
en donde b >0 y b ≠ 1. Claro que cuando b = e, loge x = lnx.
Con base en lo anterior no es difícil comprender las siguientes propiedades de los
logaritmos:
13

14. • logb (xy) = logb x + logb y
⎛x⎞
• logb ⎜ ⎟ = logb x − logb y
⎝y⎠
• logb x n = nlogb x
Ejercicios 4
1. Dibuja las gráficas de ex y de lnx y en ellas muestra que elnu = u.
Con base en el comportamiento de sus gráficas contesta las siguientes preguntas:
2. ¿La función lnx es creciente o decreciente?
3. ¿Qué concavidad tiene la función lnx?
4. ¿lnx tiene puntos de inflexión?
La derivada de las funciones exponenciales y = ex, y = eu
Para determinar la derivada de las funciones exponenciales iniciamos encontrando
la de la función f(x) = ex, procederemos utilizando la definición de derivada:
f(x + h) − f(x) e x +h − e x
f´(x) = lim = lim
h →0 h h →0 h
Ahora bien, como ex+h – ex = ex(eh - 1), y ex no varia conforme h tiende a cero,
podemos escribir
e x +h − e x eh − 1
f´(x) = lim = e lim
x
h →0 h h →0 h
eh − 1
Sólo nos falta determinar el lim , para lo cual hacemos lo siguiente: Primero
h→0 h
al resultado de eh –1 le llamamos k, esto es: eh –1 = k, de donde eh = 1 + k. De lo
anterior ln(eh) = ln(1 + k), por lo que considerando las propiedades de los
logaritmos obtenemos que h = ln(1 + k). Además, si h → 0, k = eh –1 → 0 (¿por
qué). Considerando lo anterior y una propiedad de los logaritmos (n lnx = lnxn),
substituimos en nuestro límite para obtener:
eh − 1 k 1 1
lim = lim = lim = lim
h →0 h k →0 ln(1 + k) k →0 1 k →0 1
ln(1 + k) ln(1 + k)k
k
Asignémosle el valor 1/k a n, esto es n = 1/k, por lo que k = 1/n. Observemos que
n
⎛ 1⎞
cuando k → 0, n = 1/k → ∞ , recordemos que e = lim ⎜ 1 + ⎟ y utilicemos las
n→∞
⎝ n⎠
propiedades de los límites para obtener lo siguiente:
1 1 1 1
lim = = = =1
k →0 1
⎡ 1
⎤ ⎡ 1 n ⎤ ln e
ln(1 + k)k lim ⎢ln(1 + k)k ⎥ n→∞ ⎢ln(1 + ) ⎥
lim
k →0 ⎣ n ⎦
⎣ ⎦
14

15. Este resultado nos permite concluir que
e x +h − e x eh − 1
f´(x) = lim = e x lim = ex ,
h →0 h h →0 h
es decir
d x
e = ex
dx
Este resultado es inesperado. Significa que la pendiente de la recta tangente a la
curva de la función f(x) = ex en el punto (x0,f(x0)) es m = e x0 . ¡Su primera derivada,
segunda,...,n-ésima sigue siendo la misma función!
Ejemplo 15. Determina de la función f(x) = ex
a) Su concavidad.
b) Sus máximos y mínimos.
c) Sus puntos de inflexión.
d) Si es creciente o decreciente.
Solución.
a) Como f’’(x) = ex siempre es mayor que cero, es cóncava hacia arriba.
b) Como f’(x) > 0, para toda x, y f’(x) está definida para toda x real, f(x) no tiene
números críticos, en consecuencia no tiene valores extremos, es decir, no tiene
máximos ni mínimos.
c) Lo mismo pasa para f’’(x), como f’’(x) ≠ 0 para todo x, f(x) = ex no tiene puntos
de inflexión.
d) Finalmente, como f’(x) = ex es mayor que cero para toda x, f es estrictamente
creciente.
Ahora, utilizando la regla de la cadena encontraremos la derivada de eu:
d u deu du du
(e ) = = eu
dx du dx dx
A continuación aplicaremos estas fórmulas en varios ejemplos.
Ejemplo 16. Encuentra la derivada de cada una de las siguientes funciones:
a) f(x) = 4ex b) f(x) = e5x c) f(x) = e-2x
1 2
e) f ( x ) = 3e x f) f(x) = 5e3x −5x+2
d) f(x) = 2e x
2x+4 1+ x 2
3 x −1
g) f ( x ) = e i) f ( x ) = e x
h) f ( x ) = e 1− x
Solución. Para resolver las derivadas es necesario que recuerdes las siguientes
fórmulas de derivación:
d d
• axn = a xn = anxn−1 .
dx dx
15

16. du
d
• u = dx .
dx 2 u
du dv
v −u
d u
• = dx 2 dx .
dx v v
d d d
• uv = u v + v u.
dx dx dx
d d
a) 4e x = 4 e x = 4e x .
dx dx
d 5x d
b) e = e5 x 5x = e5 x 5 = 5e5 x .
dx dx
d −2x d
c) e = e −2x ( −2x) = e−2x ( −2) = −2e−2x .
dx dx
1
1 1 1 1 1
d d d ⎛ 1⎞ d −1 −2 2e x
d) 2e = 2 e = 2e
x
⎜ x ⎟ = 2e dx x = 2e ( −1x ) = − x 2 .
x x x x
dx dx dx ⎝ ⎠
d d x x d 1 3e x
e) 3e = 3 e = 3e
x
x = 3e x
= .
dx dx dx 2 x 2 x
d 2 d 2 2 d
f) 5e−3x −5x+2 = 5 e−3x −5x+2 = 5e−3x −5x+2 (−3x2 − 5x + 2) =
dx dx dx
−3x2 −5x + 2 2
= 5e (−6x − 5) = −(6x + 5) 5e−3x −5x+2 .
d
(2x + 4)
d 2x + 4 d 2 e 2x + 4
g) e = e 2x + 4 2x + 4 = e 2x + 4 dx = e 2x + 4 = .
dx dx 2 2x + 4 2 2x + 4 2x + 4
d d
1+ x 1+ x 1+ x (1 − x) (1 + x) − (1 + x) (1 − x)
d d ⎛ 1+ x ⎞ dx dx
h) e 1− x
=e 1− x
=e 1− x
=
dx dx ⎜ 1 − x ⎟
⎝ ⎠ (1 − x) 2
1+ x 1+ x
(1 − x)(1) − (1 + x)( −1) (1 − x) − ( −1 − x)
= e1− x = e1− x
(1 − x) 2
(1 − x)2
1+ x
1+ x 1+ x
1− x + 1+ x 2 2e1− x
=e 1− x
= e1− x = .
(1 − x)2 (1 − x)2 (1 − x)2
d x2 3x −1 2 d 2 2 ⎛ d d ⎞
i) e = e x 3x −1 x 3x − 1 = e x 3x −1 ⎜ x 2 3x − 1 + 3x − 1 x 2 ⎟ =
dx dx ⎝ dx dx ⎠
⎛ d ⎞
2 ⎜ 2 dx (3x − 1) ⎟ 2 ⎛ 3x 2 ⎞
= e x 3x −1 ⎜ x + 3x − 1(2x) ⎟ = e x 3x −1 ⎜ + 2x 3x − 1 ⎟ =
⎜ 2 3x − 1 ⎟ ⎝ 2 3x − 1 ⎠
⎜ ⎟
⎝ ⎠
16

17. 2
3x −1
⎛ 3x 2 2x 3x − 1(2 3x − 1) ⎞ x 2 3x −1 ⎛ 3x + 4x(3x − 1) ⎞
2
= ex ⎜ + ⎟=e ⎜ ⎟=
⎜ 2 3x − 1 2 3x − 1 ⎟ 2 3x − 1
⎝ ⎠ ⎝ ⎠
2
3x −1 ⎛ 3x + 12x − 4x) ⎞ (15x 2 − 4x)e x 3x −1
2 2
2
= ex ⎜ ⎟=
⎝ 2 3x − 1 ⎠ 2 3x − 1
Ejercicios 5
Encuentra la derivada de cada una de las siguientes funciones:
1. f(x) = 3e3x. 2. f(x) = e-5x. 3. f(x) = e-3/x
2
6. f(x) = e 4x −3x +5
3 2
− 5. f(x) = 3e 3− x
4. f(x) = 2e x
3x − 4 2+ x 2
3x −1
7. f(x) = e 9. f(x) = e x
8. f(x) = e 2− x
Las derivadas de y = lnx, y = lnu, y = logbu,
Determinemos la derivada de f(x) = eln x :
d ln x d
e = eln x ln x
dx dx
Ahora, como x = eln x , tenemos que
d d ln x d
x= e = eln x ln x
dx dx dx
d d
1 = eln x ln x = x ln x
dx dx
Por lo tanto
d 1
ln x = .
dx x
Si utilizamos la regla de la cadena podemos encontrar la derivada de lnu como
sigue:
d d d 1 d
lnu = lnu u = u.
dx du dx u dx
Ejemplo 17. Determina las derivadas de las siguientes funciones.
a) f(x) = lnx2 b) f(x) = ln2x3 c) f(x) = ln(4x2 – 3x + 5)
3ln 4x
d) f(x) = x 2 ln x e) f(x) = 3e4x ln x f) f(x) =
ex
⎛ 1+ x2 ⎞
( )
5
g) f(x) = ln x 3
h) f(x) = ln ⎜ ⎟ i) f(x) = ln 3x 2 − 5x + 4
⎝ 1− x2 ⎠
Soluciones.
d 1 d 2 1 2x 2
a) ln x 2 = 2 x = 2 2x = 2 = ,
dx x dx x x x
17

18. o bien utilizando propiedades de la función logaritmo;
d d d 1 2
ln x 2 = 2ln x = 2 ln x = 2 = .
dx dx dx x x
d 2 3 d 1 d 3 1
b)
dx
ln x = 2ln x3
dx
ln x 3 = 2ln x 3 3
x dx
( )
x = 2ln x 3 3 (3x 2 ) = .
x
2 3 3
6x ln x 6ln x 18ln x
= 3
= = .
x x x
O bien,
d 2 3 d d d 1 18ln x
ln x = 2ln x3 ln x 3 = 6ln x 3ln x = 6ln x(3 ln x) = (18ln x) = .
dx dx dx dx x x
d 1 d
c) ln(4x 2 − 3x + 5) = 2 (4x 2 − 3x + 5) =
dx 4x − 3x + 5 dx
1 8x − 3
= 2 (8x − 3) = 2 .
4x − 3x + 5 4x − 3x + 5
d 2 d d 2 1
d) x ln x = x 2 ln x + ln x x = x 2 + ln x(2x) = x + 2x ln x = x(1 + 2ln x) .
dx dx dx x
d d d 1 d
e) 3e4x ln x = 3e4x ln x + ln x 3e4x = 3e4x + ln x(3e4x 4x) =
dx dx dx x dx
3e4x 3e4x ⎛1 ⎞
= + ln x(12e4 x ) = + 12e4x ln x = 3e4x ⎜ + 4ln x ⎟ .
x x ⎝x ⎠
d d x 4
ex ln 4x − ln 4x e e x − (ln 4x)e x
d 3ln 4x d ln 4x
f) =3 = 3 dx dx = 3 x 2x =
dx e x dx e x (e x )2 e
4e x 4e x xe x ln 4x 4e x − xe x ln 4x
− e ln 4x
x
−
=3 x =3 x x =3 x =
e2x e2x e2x
4e x − xe x ln 4x e x (4 − x ln 4x) 3(4 − x ln 4x)
=3 =3 = .
xe2x xe2x xe x
d d d 3 405 4
( )
5
g) ln x 3 = 5(ln x3 )4 ln x 3 = 5(ln x 3 )4 3ln x = 5(3ln x)4 = ln x .
dx dx dx x x
d ⎛ 1+ x2 ⎞ d d d
h) ln ⎜ 2 ⎟
dx ⎝ 1 − x ⎠ dx
= ( )
ln(1 + x 2 ) − ln(1 − x 2 ) =
dx
ln(1 + x 2 ) −
dx
ln(1 − x 2 ) =
2x −2x 2x(1 − x 2 ) + 2x(1 + x 2 )
= − = =
1+ x2 1− x2 (1 + x 2 )(1 − x 2 )
2x − 2x 3 + 2x + 2x 3 4x 4x
= = = .
(1 + x )(1 − x )
2 2
(1 + x )(1 − x ) 1 − x 4
2 2
1
d d 1 d
i) ln 3x 2 − 5x + 4 = ln(3x 2 − 5x + 4) 2 = ln(3x 2 − 5x + 4) =
dx dx 2 dx
1 d 6x − 5
= (3x 2 − 5x + 4) =
2(3x − 5x + 4) dx
2
2(3x 2 − 5x + 4)
18

19. A continuación vamos a encontrar la derivada de la función f(x) = bx, y luego la de
bu. Para hacerlo, utilizaremos la derivada de la función lnbx:
d 1 d x
lnbx = x b .
dx b dx
Por otro lado,
d d d
lnb x = x lnb = lnb x = lnb,
dx dx dx
y como b es una constante, también lo es lnb.
Así pues,
d 1 d x
lnb x = x b = lnb,
dx b dx
de donde
d x
b = bx ln b
dx
Podemos generalizar la fórmula anterior, derivando la función bu, utilizando la
regla de la cadena:
d u d u d d
b = b u = bu lnb u.
dx du dx dx
Para determinar la derivada de f(x) = logbx, hacemos uso de la derivada de bx y de
que blogb x = x como sigue. Tomando en cuenta que
d logb x d
b = x = 1,
dx dx
y que
d logb x d d
b = blogb x lnb logb x = x lnb logb x ,
dx dx dx
llegamos a
d
1 = x lnb logb x ,
dx
de donde
d 1
logb x = .
dx x lnb
Utilizando la regla de la cadena, se puede llegar a la siguiente derivada:
d 1 d
logb u = u
dx ulnb dx
Uno de los ejercicios que te dejamos es encontrar la fórmula anterior.
19

20. Ejemplo 18. Determina las derivadas de las siguientes funciones.
a) f(x) = 2x b) f(x) = 42x-3 c) f(x) = 7 x
d) f(x) = log2 x e) f(x) = log3 (2x 3 − 3) f) f(x) = log5 x
Solución.
d x
a) 2 = 2x ln 2 .
dx
d 2x −3 d
b) 4 = 42x −3 ln 4 (2x − 3) = (2ln 4)42x −3 = (ln16)42x −3 .
dx dx
d x d ⎛ 1 ⎞ 7 x ln7
c) 7 = 7 x ln7 x = 7 x ln7 ⎜ ⎟= .
dx dx ⎝2 x⎠ 2 x
d 1
d) log2 x = .
dx x ln2
d 1 d 6x
e) log3 (2x 3 − 3) = (2x 3 − 3) = .
dx (2x − 3)ln3 dx
3
(2x − 3)ln3
3
d 1 d 1 1 1
f) log5 x = x= = , o bien
dx x ln5 dx x ln5 2 x 2x ln5
d 1 d 1 1 1
log5 x = log5 x = =
dx 2 dx 2 x ln5 2x ln5
Ejercicios 6
1. Encontrar la derivada de las siguientes funciones:
a) f(x) = lnx3 b) f(x) = ln3x2 c) f(x) = ln(3x2 – 2x - 4)
d) f(x) = 4x 3 ln x e) f(x) = 2e−4x ln x 2ln3x
f) f(x) =
ex
g) f(x) = ( ln x 2 ) ⎛ 1− x2 ⎞
4
h) f(x) = ln ⎜ i) f(x) = ln x3 − 3x 2 + 2
2 ⎟
⎝ 1+ x ⎠
j) f(x) = 5x k) f(x) = 63x-4 l) f(x) = 9 5x
m) f(x) = log10 x n) f(x) = log4 (2x 3 − 3x)
o) f(x) = log5 x 3
d 1
2. Utilizando la regla de la cadena demuestra que si logb x = , entonces
dx x lnb
d 1 d
logb u = u
dx ulnb dx
3. Encuentra la derivada de la función f(x) = xx, en donde x > 0.
4. Encuentra la derivada de ux.
Derivación logarítmica y sus aplicaciones.
Existen funciones en las que para derivarlas podemos apoyarnos en las
propiedades de las funciones logarítmicas. A continuación te presentamos
ejemplos de esto.
20

21. Ejemplo 19. Determina la derivada de la función f(x) = x4x, con x > 0.
Solución.
Para determinar la derivada de y = x4x, le aplicamos la función logaritmo a ambos
lados de la igualdad
lny = ln x4x,
luego aplicamos una de las propiedades de los logaritmos (¿cuál?) y a
continuación derivamos
lny = 4x lnx,
d d
ln y = 4 x ln x
dx dx
1 d d
y = 4(x ln x + ln x)
y dx dx
1 d 1 d
y = 4(x( ) x + ln x)
y dx x dx
d
y = 4y(1 + ln x )
dx
d
y = 4x 4x (1 + ln x)
dx
Ejemplo 20. Encuentra la derivada de la función y = (x+4)lnx.
Solución.
Aplicamos la función logaritmo, sus propiedades y derivamos.
ln y = ln(x + 4)ln x
ln y = (ln x)ln(x + 4)
d d
ln y = (ln x)ln(x + 4)
dx dx
1 d d d
y = ln x ln(x + 4) + ln(x + 4) ln x
y dx dx dx
1 d 1 d 1
y = (ln x) (x + 4) + ln(x + 4)
y dx x + 4 dx x
1 d 1 1
y = (ln x) + ln(x + 4)
y dx x+4 x
d ⎛ 1 1 ⎞
y = y⎜ ln x + ln(x + 4) ⎟
dx ⎝x+4 x ⎠
d ⎛ 1 1 ⎞
y = ln(x + 4)ln x ⎜ ln x + ln(x + 4) ⎟
dx ⎝x+4 x ⎠
Ejercicios 7
Utilizando la derivación logarítmica y suponiendo que x > 0, encuentra la derivada
de:
x
1. y = x e
21

22. 2. y=x x.
3. y = x1/x.
4. y = x1/lnx.
5. y = xu.
Bibliografía
1. Allan B. Cruse y Millianne Lehman. “Lecciones de Cálculo 1”. Fondo de Cultura
Educativo Iberoamericano, México 1987. Lección 16.
2. James Stewart. “Cálculo. Conceptos y Contextos”. Thomson, México, 1999.
Secciones 1.5, 1.6, 3.1, 3.4 y 3.7.
3. Larry Goldstein, et al. “Cálculo y sus aplicaciones”. Prentice Hall
Hispanoamericana. México 1990. Capítulos 4 y 8.
4. Larson Hostetler Edwards. “Cálculo”. McGraw – Hill, México, 1999. Secciones
3.4, 5.7, 5.8, 5.9, 6.1 y 6.2.
22