EJERCICIOS PROPUESTOS

1. v4
v5
v6
v7
v8

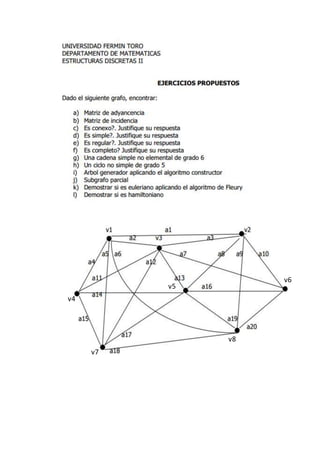
2. Matriz de adyacencia
v1 v2 v3 v4 v5 v6 v7 v8
v1 0 1 1 1 0 0 1 1
v2 1 0 1 0 1 1 0 1
v3 1 1 0 1 1 1 1 0
v4 1 0 1 0 1 0 1 0
v5 0 1 1 1 0 1 1 1
v6 0 1 1 0 1 0 0 1
v7 1 0 1 1 1 0 0 1
v8 1 1 0 0 1 1 1 0
Matriz de incidencia
v1 v2 v3 v4 v5 v6 v7 v8
a1 1 1 0 0 0 0 0 0
a2 1 0 1 0 0 0 0 0
a3 0 1 1 0 0 0 0 0
a4 1 0 0 1 0 0 0 0
a5 1 0 0 0 0 0 1 0
a6 1 0 0 0 0 0 0 1
a7 0 0 1 0 0 1 0 0
a8 0 1 0 0 1 0 0 0
a9 0 1 0 0 0 0 0 1
a10 0 1 0 0 0 1 0 0
a11 0 0 1 1 0 0 0 0
a12 0 0 1 0 0 0 1 0
a13 0 0 1 0 1 0 0 0
a14 0 0 0 1 1 0 0 0
a15 0 0 0 1 0 0 1 0
a16 0 0 0 0 1 1 0 0
a17 0 0 0 0 1 0 1 0
a18 0 0 0 0 0 0 1 1
a19 0 0 0 0 1 0 0 1
a20 0 0 0 0 0 1 0 1

3. El grafo es conexo pues todos sus vértices son accesibles desde cada uno de
ellos.
Es simple completo por que no tiene lazos ni aristas repetitivas.
No es un grafo regular debido a que las vértices no tienen el mismo grado.
Cadena no elemental de grado 6:
C1=[v1,a4,v4,a14,v5,a13,v3,a2,v1,a1,v2,a8,v5]
Cadena no simple de grado 5:
C2=[v3,a3,v2,a10,v6,a16,v5,a13,v3,a3,v2]
Árbol generador algoritmo constructor:
Seleccionamos v1, H1={v1}
Seleccionamos la arista a1 H2={v1,v2}
Arista a3
H3={v1,v2,v3}
Arista a13
H4={v1,v2,v3,v5}
v1
v2
a1
v1
v2
a1
a3
v3
v1
v2
a1
a3
v3
v5
a13

4. Arista a16
H5={v1,v2,v3,v5,v6}
Arista a20
H6={v1,v2,v3,v5,v6,v8}
Arista a18
H7={v1,v2,v3,v5,v6,v8,v7}
Arista a15
H8={v1,v2,v3,v5,v6,v8,v7,v4}
Finalmente obtenemos H8 que es el árbol generador que contiene todos los
vértices.
v1
v2
a1
a3
v3
v5
a13
a16
v6
v1
v2
a1
a3
v3
v5
a13
a16
v6
a20
v8
v1
v2
a1
a3
v3
v5
a13
a16
v6
a20
v8
a18
v7
v1
v2
a1
a3
v3
v5
a13
a16
v6
a20
v8
a18
v7
a15
V4

5. Subgrafo parcial
Demostrar si el grafo es euleriano mediante Fleury:
Luego de realizar múltiples recorridos para tratar de cumplir con las reglas del
algoritmo se puede concluir que el grafo no es euleriano, debido a que no se
pueden recorrer todas las aristas sin repetirlas.
Demostrar si es hamiltoniano:
El grafo es hamiltoniano por que contiene al menos un ciclo hamiltoniano.
C={v1,a1,v2,a3,v3,a13,v5,a7,v6,a20,v8,a18,v7,a15,v4,a4,v1}
v1
v2
a1
a3
v3
v5
a13
a16
v6
v8
a18
v7
a15
V4
v1
v2a1
a3
v3
v5
a13
a7
v6
v8
a20
v7
a18
V4
a15
a4

7. Matriz de conexión:
v1 v2 v3 v4 v5 v6
v1 0 1 1 0 1 0
v2 0 0 1 1 0 1
v3 0 0 0 1 1 0
v4 1 0 0 0 0 1
v5 0 1 0 1 0 1
v6 0 0 0 0 1 0
El grafo dado es simple, debido a que este no tiene lazos ni aristas en paralelo
entre los vértices.
Cadena no simple no elemental de grado 5:
C={v5,a13,v6,a14,v5,a11,v4,a12,v6,a14,v5}
Ciclo simple:
Cs={v1,a5,v3,a8,v4,a9,v1}

8. Matriz de accesibilidad:
Matriz de conexion:
Mc(D)=
Resolvamos la siguiente fórmula para demostrar si es fuertemente conexo
𝑀2( 𝐷) =
v1 v2 v3 v4 v5 v6
v1 0 1 1 0 1 0
v2 0 0 1 1 0 1
v3 0 0 0 1 1 0
v4 1 0 0 0 0 1
v5 0 1 0 1 0 1
v6 0 0 0 0 1 0
v1 v2 v3 v4 v5 v6
v1 0 1 1 1 1 1
v2 1 0 0 1 1 1
v3 1 1 0 1 0 1
v4 0 1 1 0 1 0
v5 1 0 1 1 1 1
v6 0 1 0 1 0 1

9. 𝑀3( 𝐷) =
𝑀4( 𝐷) =
𝑀5( 𝐷) =
v1 v2 v3 v4 v5 v6
v1 1 1 1 1 1 1
v2 1 1 1 1 1 1
v3 1 1 1 1 1 1
v4 0 1 1 1 1 1
v5 1 1 1 1 1 1
v6 1 0 1 1 1 1
v1 v2 v3 v4 v5 v6
v1 1 1 1 1 1 1
v2 1 1 1 1 1 1
v3 1 1 1 1 1 1
v4 1 1 1 1 1 1
v5 1 1 1 1 1 1
v6 1 1 1 1 1 1
v1 v2 v3 v4 v5 v6
v1 1 1 1 1 1 1
v2 1 1 1 1 1 1
v3 1 1 1 1 1 1
v4 1 1 1 1 1 1
v5 1 1 1 1 1 1
v6 1 1 1 1 1 1

10. 𝑀6( 𝐷) =
𝐴𝑐𝑐( 𝐷) = 𝑏𝑖𝑛
𝐴𝑐𝑐( 𝐷) =
Como la matriz no tiene componentes nulas entonces se puede decir que es
fuertemente conexo.
v1 v2 v3 v4 v5 v6
v1 1 1 1 1 1 1
v2 1 1 1 1 1 1
v3 1 1 1 1 1 1
v4 1 1 1 1 1 1
v5 1 1 1 1 1 1
v6 1 1 1 1 1 1
v1 v2 v3 v4 v5 v6
v1 4 6 6 5 6 5
v2 6 4 5 6 5 6
v3 5 5 4 6 5 5
v4 4 5 5 4 5 4
v5 5 5 5 6 5 6
v6 4 4 4 5 5 5
v1 v2 v3 v4 v5 v6
v1 1 1 1 1 1 1
v2 1 1 1 1 1 1
v3 1 1 1 1 1 1
v4 1 1 1 1 1 1
v5 1 1 1 1 1 1
v6 1 1 1 1 1 1