Este documento presenta 6 problemas resueltos relacionados con la suma de vectores utilizando el método analítico. En el primer problema se aplica la ley del seno para encontrar el ángulo entre dos vectores dados sus magnitudes y la magnitud de su resultado. En el segundo problema también se usa la ley del coseno. El tercer problema involucra descomponer vectores en componentes rectangulares y realizar operaciones. Los últimos tres problemas usan descomposición vectorial para encontrar magnitudes y ángulos desconocidos.

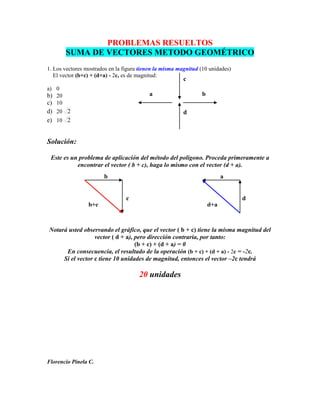
1. PROBLEMAS RESUELTOS
SUMA DE VECTORES METODO GEOMÉTRICO
1. Los vectores mostrados en la figura tienen la misma magnitud (10 unidades)
El vector (b+c) + (d+a) - 2c, es de magnitud:
c
a) 0
b) 20 a b
c) 10
d) 20 2 d
e) 10 2
Solución:
Este es un problema de aplicación del método del polígono. Proceda primeramente a
encontrar el vector ( b + c), haga lo mismo con el vector (d + a).
b a
c d
b+c d+a
Notará usted observando el gráfico, que el vector ( b + c) tiene la misma magnitud del
vector ( d + a), pero dirección contraria, por tanto:
(b + c) + (d + a) = 0
En consecuencia, el resultado de la operación (b + c) + (d + a) - 2c = -2c.
Si el vector c tiene 10 unidades de magnitud, entonces el vector –2c tendrá
20 unidades
Florencio Pinela C.

2. 2. Si el ángulo con el que un objeto rebota es el mismo con el que incide,
con respecto a un eje perpendicular a la superficie de impacto. ¿Cuál de los
siguientes vectores representaría mejor al vector V2 - V1?, donde V2 es la
velocidad con que rebota de la superficie II.
II
V1
I
a) b) c) d) cero e)
Solución: V2
II
V1
I
Para poder realizar la diferencia entre los dos vectores, necesitamos conocer la
magnitud y dirección del vector velocidad con que el objeto rebota de la segunda pared.
Tracemos entonces la trayectoria del objeto luego de rebotar de las dos superficies,
como se indica en el gráfico superior. Una vez obtenido el vector V2, la velocidad con
que rebota de la segunda pared, podemos obtener la diferencia entre ellos.
Recordemos que la diferencia de dos vectores es equivalente a la suma de uno de ellos
con el negativo del otro
Florencio Pinela C.

3. Al realizar la diferencia entre el vector V2 y el vector V1 por el método geométrico, tenemos:
-V1
V2
V2 + (-V1)=
La respuesta se aproxima a la alternativa C
3. Los vectores A, B y C se muestran en la figura, cuyas magnitudes son 10
unidades, 15 unidades y 20 unidades respectivamente. El vector A –
B – C es:
a) 5 unidades dirigido hacia la derecha
b) 25 unidades dirigido hacia la izquierda C A B
c) 15 unidades dirigido hacia la derecha
d) 40 unidades dirigido hacia la derecha
e) 5 unidades dirigido hacia la izquierda
Solución:
Realicemos la operación utilizando el método del polígono, unamos el extremo de un
vector con el origen del otro (de acuerdo a la operación que nos estén pidiendo
realizar), el vector – C lo ubicamos ligeramente debajo para que no oculte a los otros
vectores en el diagrama, el vector resultante es el que se dirige desde el origen del
primero al extremo del último
15 10
-B A
-C
20
Sería un vector de 5 unidades dirigido a la izquierda
Florencio Pinela C.

4. 4. Para los vectores mostrados en la figura. ¿Cuál de las siguientes alternativas
es la correcta?
a) j + g - c = a + 2e
b) b+f-i=j+h-a
c) a + b + c = 2g
d) a+b+d+e=f+h+i
e) b+f+i=a+j+h
Solución:
Tomemos una de las alternativas múltiples para ilustrar la aplicación del método del
polígono a este problema, escojamos la alternativa a) j + g - c = a + 2e, podemos
comenzar pasando el vector –c al lado derecho de la igualdad
j + g = a + 2e + c
Comprobemos gráficamente si el vector ( j + g) es igual al vector ( a + 2e + c)
( a+2e+c)
g
(j +g) c
a
j 2e
Como podemos observar en los gráficos estos vectores no son iguales, en consecuencia
la alternativa a) no es correcta, a continuación mostramos el desarrollo de la
alternativa verdadera.
c
g
La alternativa correcta
es la C b
g
a
Florencio Pinela C.

5. PROBLEMAS PROPUESTOS
SUMA DE VECTORES METODO GRAFICO
1. Todos los vectores que forman el cuadrado mostrado en la figura tienen una magnitud
de 10 unidades. La resultante de la suma de los cinco vectores es:
a) 10 2
b) 20
c) 10
d) 5 2
e) 5
2. Para el conjunto de vectores mostrado en la figura, el vector D que equilibra (que al
sumarse da una resultante nula) al conjunto de vectores es:
a) 2i – 4j 4u
b) 2i + 4j A
c) –2i + 4j
d) –2i – 4j
e) 2i + 2j B 4u
2u C
3. En el triángulo isósceles OAB, los lados OA y OB son iguales, y M es el punto medio
del lado AB. ¿Cuál de las siguientes alternativas es correcta?
a) m=a+b
b) m = ½ (a + b) A M
c) m = ½ (a - b) B
d) a+b+m=0
e) m·(b-a)=0 a m b
O

6. 4. Para los vectores dados en la figura, la alternativa correcta es:
a) a+e+j=c a b
b) c + h + f = a + b
h
c) e+j=c+a c d e f
d) b + d -f -j = 0
e) c + h + f = b - a j
5. Los vectores mostrados en la figura están inscritos en una circunferencia de radio R.
La magnitud de la resultante de la suma de los cinco vectores es:
a) R diámetro
b) 2R
c) 3R
d) 4R
e) 5R
6. Sean los vectores A y B; el vector A tiene 10 unidades de magnitud. El vector
A – B es perpendicular al vector A y tiene 15 unidades de magnitud. La magnitud del vector B es
a) 18.0
b) 16.0
c) 13.0
d) 11.2
e) 8.0

7. PROBLEMAS RESUELTOS
SUMA DE VECTORES METODO ANALÍTICO: LEY DEL
SENO, LEY DEL COSENO Y DESCOMPOSICIÓN
VECTORIAL
1. Dos vectores a y b tienen 10 y 15 unidades respectivamente, si la
resultante de la suma de los vectores tiene 20 unidades, el ángulo
entre los vectores es
a) 75,5º
b) 70,0º
c) 65,5º
d) 60,0
e) 55,5º
Solución:
En este problema disponemos de las magnitudes de los dos vectores componentes y de
la resultante de la suma de ellos. Un problema típico de aplicación de la ley del coseno.
Recuerde que la ley del coseno relaciona las magnitudes de los vectores componentes y
de la resultante, a sí como del ángulo formado entre los vectores componentes.
Llamemos c al vector resultante de la suma de los vectores a y b
  
c a b
De la ley del coseno
C2 = a2 + b2 + 2ab cos
representa el ángulo formado entre los dos vectores a y b unidos por su origen.
c2 a2 b2
cos( )
2ab
20 2 10 2 15 2
cos( )
2 *10 * 15
cos( ) 0.25
= 75,5
Florencio Pinela C.

8. 2. Para el paralelepípedo de la figura, determine el ángulo formado entre los
vectores a y b.
a) 45,0º
b) 48,2º
c) 50,2º
d) 53,8º
e) 55,2º y
6
a
x
b
4
z 5
Solución:
Apliquemos nuevamente la ley del coseno para encontrar el ángulo entre los vectores.
Aquí necesitamos conocer las magnitudes de los vectores a y b y de la resultante de la
suma de ellos. Con los valores de los lados del paralelepípedo obtenemos los vectores a
y b en función de sus componentes rectangulares, una vez determinados a y b pasamos
a calcular la resultante de la suma de los dos, digamos el vector c; (c = a + b).
a = 6j – 4k a2 = 62 +42 a= 62 4 2 = 7,21
b = 5i + 6j b2 = 52 + 62 b= 52 6 2 = 7,81
Llamamos c al vector (a + b) = 5i + 12j – 4k c= 52 12 2 4 2 = 13,60
Utilizando la ley del coseno
C2 = a2 + b2 + 2ab cos
Despejando el coseno de y reemplazando los módulos de los vectores a,b y c
Cos = (185-52-61)/112,62
Cos = 0,64
Por tanto es igual a 50,2
Florencio Pinela C.

9. 3. Para los vectores mostrados en la figura, el vector que representa la
operación: a - b/2 es
y
6
a) 6 i - 9 j + 12 k
b) 3 i + 12 j +6 k
c) 6i - 9j + 4 k
d) 4 i + 8 j +12 k b
4
x
e) 8 i + 5 j + 10 k
a
8
z
Solución:
Los vectores a y b se encuentran dentro del paralelepípedo, observando el origen y el
extremo de cada uno de ellos podemos determinar sus componentes rectangulares (las
proyecciones del vector sobre cada uno de los ejes coordenados), por ejemplo: la
componente sobre el eje “y” del vector a vale 6 y apunta en dirección negativa (-j).
Para determinar las componentes sobre los ejes “x” y “z”, proyectemos el vector sobre
el plano x-z, seguidamente podemos observar que la componente sobre el eje “x” vale 4
y apunta en la dirección +i, y la componente sobre el eje “z” vale 8 y apunta en la
dirección +k. De esta manera podemos escribir los vectores:
a = 4i –6j +8k
b = -4i +6j +8k
El vector b/2 lo obtenemos dividiendo cada uno de los módulos de sus componentes
para 2 b/2 = -2i +3j +4k
Por tanto (a – b/2) = 4i – 6j +8k +2i – 3j – 4k
a – b/2 = 6i –9j +4k  la respuesta es la c
4. Para el problema anterior, el ángulo formado entre los vectores a y b es
a) 128 º
b) 84º
c) 56º
d) 48º
e) 38º
Florencio Pinela C.

10. Solución:
Tomando los vectores a y b, vamos a aplicar la ley del coseno para determinar el
ángulo entre estos vectores. Determinemos primeramente la resultante de sumar los
dos vectores.
a = 4i –6j +8k a2 = 116
b = -4i +6j +8k b2 = 116
c = (a + b) = 4i – 6j + 8k -4i +6j +8k
c = 0i + 0j + 16k c = 16
c2 = a2 + b2 + 2ab cos
Despejando el cos y reemplazando las magnitudes de a, b y c
Obtenemos cos = (256-116-116)/2*116
cos = 0,103
Por tanto = 84
5. Los vectores mostrados en la figura al sumarse dan una resultante nula. La
magnitud y dirección del vector A es.
y
a) 60,3 u. ; 25,6º 40 u
b) 60,3 u ; 108,2º
A
c) 47,7 u ; 205,6º
d) 50,5 u ; 18,2º 50
e) 50,5 u ; 198,2º
x
30
20 u
Solución:
Utilizando el método de descomposición vectorial podemos obtener dos ecuaciones,
una para las componentes en “x”, y la otra para las componentes en “y”. Obtenidas las
componentes en “x” y en “y” del vector, utilizaremos el teorema de Pitágoras para
calcular la magnitud del vector A, y luego valiéndonos de una función trigonométrica
podemos determinar la dirección del vector.
Si los tres vectores al sumarse dan una resultante nula (R = 0), esto significa que sus
componentes también deben serlo, esto es:
Rx = 0, la suma de todas las componentes en “x” deben dar cero
Ry = 0, la suma de todas las componentes en “y” deben dar cero.
Rx = Ax + 40 cos50° + 20 cos(-30°) = 0
Ry = Ay + 40 sen50° + 20 sen(-30°) = 0

11. Ax + 25,71+ 17,32= 0 Ax=- 43,03
Ay + 30,64 - 10= 0 Ay = - 20,64
representa el ángulo que forma el vector A con el eje positivo de las “x”.
Los ángulos son positivos cuando se miden en sentido antihorario y negativo cuando se
miden en sentido horario.
Es conveniente ubicar estas componentes sobre ejes coordenados para identificar la
dirección del vector.
Ax 25,6
Ay
A
Utilizando el teorema de Pitágoras determinamos la magnitud del vector A
A Ax2 Ay 2
2 2
A 43,03 20,64
A = 47,72
La línea de acción del vector la determinamos utilizando una función trigonométrica,
por ejemplo
Tan = Ay/Ax= - 20,64/-43,03
= Tan-1 ( 0,479)
= 25,6
¡ Cuidado! La calculadora le da a usted la línea de acción del vector, la cual puede
coincidir con la dirección del vector, vea el grafico de los vectores en la parte superior.
Por tanto, la dirección será
= 180 + 25,6
= 205,6
Florencio Pinela C.

12. 6. Sean los vectores A = 2i – j + 3k y B = 4i + 2j – k. El ángulo que forma
el vector A+B con el eje positivo de las x es
a) 16,2º
b) 20,4º
c) 23,5º
d) 26,2º
e) 32,5º
Solución:
Observando los vectores nos podemos dar cuenta que estamos en presencia de vectores
en tres dimensiones, en consecuencia podemos utilizar los cosenos directores para
determinar la dirección del vector con cada uno de los ejes coordenados. Para utilizar
los cosenos directores debemos conocer las componentes ortogonales del vector, y por
su puesto su magnitud. Como solamente nos piden determinar el ángulo que forma el
vector A+B con el eje de las “x”, necesitamos conocer solamente la componente en “x”
del vector C, esto es Cx
Determinemos primero el vector A +B, llamemos C a este vector
C = A + B = 6i +j + 2k C = 36 1 4 = 6,4
Cx = 6, Cy = 1, Cz = 2
Recordando la definición de los cosenos directores, el ángulo que forma el vector C
con el eje positivo de las “x” es
Cx
cos( )
C
cos( ) = 6/6,4
Por tanto el ángulo es 20,4
7. Con referencia al paralelepípedo de la figura, el valor de la fuerza
resultante, esto es F1+ F2 es:
y (m)
a) 73i + 62,9j - 100.5k (N)
b) 123i + 63.5j - 15.5k (N) 5
c) 123i + 63.5j - 100.5k (N)
d) 73i + 63.5j - 15.5k (N)
e) 73i - 63.5j - 100.5k (N)
F2
F1 x (m)
F2 = 2F1 = 100 N 10
8
z (m)
Florencio Pinela C.

13. Solución:
Tenga cuidado con la magnitud de los vectores y las dimensiones del paralelepípedo,
las dimensiones del paralelepípedo en este problema sirven para indicar la dirección de
los vectores. El problema sólo nos da la magnitud de los vectores fuerza, para poder
sumarlos tenemos que expresarlos en forma vectorial, esto es:
F1 = F1 cos i + F1 cos j + F1 cos k
Donde: cos , cos y cos , los cosenos directores, los podemos determinar del gráfico
de arriba
0
cos( ) 0
5 82
2
5
cos( ) 0,53
52 82
8
cos( ) - 0,85
5 82
2
F1 = 50(0) i + 50(0,53)j + 50(-0,85)k
F1 = 26,5j – 42,5k
, , y representan los ángulos que forman cada uno de los vectores con los ejes “x”,
“y” y “z”
F2 = F2 cos i + F2 cos j + F2 cos k
10
cos( ) 0,73
2
10 52 82
5
cos( ) 0,36
10 2 5 2 8 2
8
cos( ) - 0,58
2
10 52 82
F2 = 100(0,73) i + 100(0,364) j + 100(-0,58) k
F2 = 73 i + 36,4 j – 58 k
Por tanto F1 + F2 = 73 i +62,9 j – 100,5k; alternativa a
Florencio Pinela C.

14. 8. Dos cuerdas A y B halan una caja como se indica en la figura. La cuerda
A ejerce una fuerza de (18,13 i + 8,45 j ) Newtons. Determine el valor del
ángulo , de tal forma que la resultante de la suma de las tensiones de las
dos cuerdas se encuentre en la dirección del eje x +, y tenga un módulo
de 40 Newtons
a) 10º
b) 15º A
c) 21º
d) 42º
e) 69º x
B
Solución:
De acuerdo a la información del problema, el vector A es igual a:
A = 18,13 i + 8,45 j
A 18,13i 8,45 j
  
 
Ax Ay
Si la resultante de la suma de los dos vectores se encuentra en la dirección “x” esto
significa que la componente Ay debe tener la misma magnitud que la componente By, y
direcciones contrarias, es decir que:
By = 8,45 N
Tomando la información de que la resultante apunta en dirección “x”
Ax + Bx = 40
Siendo Ax = 18,13 N
Esto significa que:
Bx = 21,87 N
Conociendo las componentes ortogonales del vector B, podemos expresarlo
B = 21,87 i + 8,45 j
Observando el gráfico del problema, el ángulo es:
Tan = By/Bx
= tan-1(8,45/21,87)
= 21,1

15. PROBLEMAS PROPUESTOS
SUMA DE VECTORES METODO ANALÍTICO: LEY DEL
SENO, LEY DEL COSENO Y DESCOMPOSICIÓN
VECTORIAL
1. La magnitud y dirección de un vector, que sumado a los vectores indicados en la
figura dan una resultante nula es y
20 u
a) 22,4 u ; 63.4º
b) 30,0 u ; 63.4º 10 u
c) 22,4 u ; - 93.4º
d) 30,0 u ; 93.4º 60º 30º
x
e) 22,4 u ; - 86.6º
2. El vector mostrado en la figura tiene una magnitud de 20 unidades. El ángulo que
forma el vector con el eje y es: y
a) 30,0º
b) 60,0º
c) 72,5º
d) 41,1º
e) 35,2º x
6
8
z
3. Para los vectores a, b, y c indicados en el plano x-y-z. La magnitud del vector
a + b – c, es
y
a) 4
b) 6 b
c) 8 5
d) 10 a
e) 12 c
x
4
z 6

16. 4. Un avión desarrolla una velocidad máxima de 800 Km/h en ausencia de viento.
Las velocidades del viento y del avión se encuentran en el plano x-y. Determine
la velocidad resultante de un avión cuando el viento sopla a 200 Km/h y a 250° de
dirección, para cuando el avión se mueve en la dirección indicada.
Magnitud (Km/h) Dirección
a) 755 -14.4° y
b) 755 -22.8°
c) 888 14.4°
d) 888 -22.8°
e) 755 10.5°
x
5. Determine la magnitud del vector que al sumarse a los vectores a y b de la figura
dan como resultado una resultante nula.
a) 15.1 u
b) 18.0 u
c) 19.0 u
d) 23.1 u
e) 25.2 u
6. Para los vectores mostrados en la figura determine la magnitud y dirección del
vector R, donde: R = 2 a – b – c/2
Magnitud Dirección y
a) 36.6 36° b=15
b) 36.6 216° 40
c) 23.8 64.3° a=10 x
d) 29.7 183°
c=20
e) 28.2 215°

17. 7. Determine el vector que al sumarse a los vectores a y b den una resultante nula.
a) i – 10j + 3k y
b) 2i – 5j + 6k
c) 5j + 6k
d) 10j – 3k
e) –10j + 3k b a
5
x
3
z 7
8. Para los vectores del problema anterior determine el ángulo formado entre los vectores
ay–b
a) 55°
b) 62°
c) 72°
d) 82°
e) 90°
9. Los tres vectores mostrados en la figura representan las fuerzas que actúan sobre un
cuerpo, la fuerza resultante, es decir, la suma de todas las fuerzas tendrá como magnitud
y
a) 38 N. 5
b) 42 N. 40N 50N
c) 48 N. 1
d) 55 N. -4 -1 1 3 x
e) 60 N. 20N

18. 10. Los vectores mostrados en la figura al sumarse dan una resultante nula, los valores de
a y son ( es el ángulo con respecto al eje x+)
y
30
a) 20.0 ; 230º
20
b) 20.1 ; -79º
c) 15.8 ; 210º
40º 60º
X
d) 18.7 ; -68º
e) 38.8 ; -71º
a

19. PROBLEMAS RESUELTOS
PRODUCTO ESCALAR Y PRODUCTO VECTORIAL
1. Dado los vectores A= 2i + aj y B= 6i, el valor de a para que la magnitud de B sea igual
a tres veces la magnitud de AxB es:
a) 3
b) 1/3
c) 6
d) 1/6
e) no puede determinarse
Solución:
La magnitud del vector B es 6. determinemos la magnitud del vector AxB
i j k
AxB = 2 0 = i (0) – j (0) + k (-6 ) = -6 k
6 0 0
La magnitud del vector AxB es 6 .
Por tanto, el valor de para que la magnitud de B sea igual a tres veces la magnitud
de AxB, es
6 = 3 (6 )
= 1/3
2. Para que los vectores: a = 6 i – 3 j + 6 k y b = i – 2 j + 3 k sean ortogonales,
debe tomar el valor de
a) –4
b) 4
c) –6
d) 6
e) –8
Solución:
De acuerdo a la definición de producto escalar, si dos vectores son ortogonales su producto
escalar es cero.
Como los vectores vienen dados en función de sus componentes ortogonales, es más práctico
utilizar la operación:
a b = axbx + ayby + az bz
ax = 6; ay = -3; az = 6
bx = ; by = -2; bz = 3
a b = 6 + 6 +18 = 0
= -4 Florencio Pinela C.

20. 3. Sean lo vectores: a = 5i - 2j + 3k y b = 2i + 5j + 6k. La proyección del vector a
sobre el vector b es.
a) 4.6
b) 3.2
c) 2.8
d) 2.2
e) 1.2
Solución:
Por definición, geométricamente, el producto escalar representa el área de un rectángulo que
tiene por uno de sus lados la magnitud de uno de los vectores, y el otro lado la proyección del
segundo vector sobre el primero.
a b
ab
ab = proyección del vector a sobre el vector b
a b = ab cos = ab b = axbx + ayby + az bz
a xbx a yby a z bz
ab =
b
(5)( 2) ( 2)(5) (3)( 6)
ab =
4 25 36
18
ab =
8,06
ab = 2,2
4. Conociendo que |A| = 10 u y |B| = 15 u, el ángulo formado entre los vectores A y B es
y
a) 90,0º
b) 86,4º
c) 80,4 B
d) 76,4º
e) 70,4º
5 x
A
Florencio Pinela C.

21. Solución:
En este problema podemos hacer uso de la definición de producto escalar. Conocemos el
módulo de los vectores y sus componentes las podemos obtener del gráfico.
A B = AB cos = AxBx + AyBy + AzBz
De acuerdo al gráfico, Ay = 0, Bz = 0
Por lo tanto AB cos = AxBx
Donde Ax = 5 y Bx = 5
(5)( 5)
Cos =
(10 )(15 )
= cos-1(0,16666)
= 80,4
5. Los vectores A, B y C se dirigen desde el origen de un sistema de coordenadas
rectangulares a los puntos (2, 3, 5), (4, -5, -6) y (-2, 6, -3) respectivamente. El
resultado de la operación (A - B) · C es:
a) 4i + 48j - 33k b) 19 c) 10 d) 9 e) 5
Solución:
Con las coordenadas del punto del extremo de cada vector, los vectores A, B y C los
expresamos como:
A = 2i + 3j + 5k
B = 4i – 5j – 6k
C = -2i + 6j – 3k
Realizamos la operación (A – B):
A – B = - 2i + 8j + 11k
Luego multiplicamos escalarmente este resultado con el vector C.
(A - B) · C = (- 2i + 8j + 11k) (-2i + 6j – 3k)
(A - B) · C = 4 + 48 – 33
(A - B) · C = 19
Florencio Pinela C.

22. 6. Dado los vectores A= 2i + aj y B= 6i, el valor de a para que la magnitud de B sea igual
a tres veces la magnitud de AxB es:
f) 3
g) 1/3
h) 6
i) 1/6
j) no puede determinarse
Solución:
La magnitud del vector B es 6. determinemos la magnitud del vector AxB
i j k
AxB = 2 0 = i(0) – j(0) + k(-6 ) = -6 k
6 0 0
La magnitud del vector AxB es 6 .
Por tanto, el valor de para que la magnitud de B sea igual a tres veces la magnitud
de AxB, es
6 = 3(6 )
= 1/3
7. Para que los vectores: a = 6 i – 3 j + 6 k y b = i – 2 j + 3 k sean ortogonales,
debe tomar el valor de
f) –4
g) 4
h) –6
i) 6
j) –8
Solución:
De acuerdo a la definición de producto escalar, si dos vectores son ortogonales su producto
escalar es cero.
Como los vectores vienen dados en función de sus componentes ortogonales, es más práctico
utilizar la operación:
a b = axbx + ayby + az bz
ax = 6; ay = -3; az = 6
bx = ; by = -2; bz = 3
a b = 6 + 6 +18 = 0
= -4 Florencio Pinela C.
8. Sean lo vectores: a = 5i - 2j + 3k y b = 2i + 5j + 6k. La proyección del vector a
sobre el vector b es.
f) 4.6

23. g) 3.2
h) 2.8
i) 2.2
j) 1.2
Solución:
Por definición, geométricamente, el producto escalar representa el área de un rectángulo que
tiene por uno de sus lados la magnitud de uno de los vectores, y el otro lado la proyección del
segundo vector sobre el primero.
a b
ab
ab = proyección del vector a sobre el vector b
a b = ab cos = ab b = axbx + ayby + az bz
a xbx a yby a z bz
ab =
b
(5)( 2) ( 2)(5) (3)( 6)
ab =
4 25 36
18
ab =
8,06
ab = 2,2
9. Conociendo que |A| = 10 u y |B| = 15 u, el ángulo formado entre los vectores A y B es
y
f) 90,0º
g) 86,4º
h) 80,4 B
i) 76,4º
j) 70,4º
5 x
A
Florencio Pinela C.
Solución:
En este problema podemos hacer uso de la definición de producto escalar. Conocemos el
módulo de los vectores y sus componentes las podemos obtener del gráfico.

24. A B = AB cos = AxBx + AyBy + AzBz
De acuerdo al gráfico, Ay = 0, Bz = 0
Por lo tanto AB cos = AxBx
Donde Ax = 5 y Bx = 5
(5)( 5)
Cos =
(10 )(15 )
= cos-1(0,16666)
= 80,4
7. El trabajo se define como el producto escalar de la fuerza por el desplazamiento.
Determine el trabajo que realiza una fuerza F = 10i + 20j + 30k (N) al actuar sobre un
cuerpo haciendo que éste se mueva desde un punto de coordenadas (2,10,-5) m hasta el
punto (-2,5,8) m.
a) 250 N.m
b) 330 N.m
c) 450 N.m
d) 500 N.m
e) 550 N.m
Solución:
El cuerpo se mueve desde el punto A(2, 10, -5), hasta el punto B(-2,5,8).
Representemos cada uno de estos puntos por los vectores:
A = 2i + 10j –5k
B= -2i + 5j + 8k
Al ir del punto A al punto B habrá experimentado un desplazamiento AB = B – A, esto
es:
AB = (-2i + 5j + 8k) – (2i + 10j – 5k)
AB = -4i – 5j + 13k
En consecuencia el trabajo debe ser:
F AB = (10 i + 20j +30k) (-4i – 5j + 13k)
Trabajo = -40 - 100 + 390 = 250 N

25. 8. Para el gráfico mostrado, evalúe el producto vectorial entre el vector F de 50 unidades
de magnitud y el vector posición r.
a) -125 2i m
y
b) 150 2 i + 125 2 j 6
c) 275 2 k
F
d) 125 2 k r
e) 150 2 i
2
-5 1 5 m
Solución:
Podríamos pensar en utilizar |Fxr| = F r sen , pero recordemos que esta expresión es
para el módulo del vector |Fxr|.
Expresemos los vectores F y r en función de sus coordenadas rectangulares.
Observe que el plano en el que están graficados los vectores, los ejes representan
unidades de longitud, el vector r se representa en su real magnitud, mientras que para
el vector F las coordenadas sirven para su dirección.
F = Fcos i + Fsen j ; representa la dirección del vector F
r = rx i + ry j
F = 50 cos45° i + 50 sen45° j = 25 2 i + 25 2 j
r = -5i + 6j
i j k
Fxr = 25 2 25 2 0 = [6(25 2 ) + 5(25 2 )]k
-5 6 0
Fxr = 275 2 k
Florencio Pinela C.

26. 9. Sean los vectores a = ( 6i + 8k ) y b = ( 2j - 5/8 k ), el resultado de la operación:
2 ( a · b ) a, es
a) 0
b) -100
c) 20
d) –60 i –80 k
e) No se puede realizar la operación.
Solución:
( a · b ) es un número, que al multiplicarlo por a debe dar un vector, de las alternativas,
sólo una da la posibilidad a que el resultado sea un vector. De todas maneras
resolvamos el problema.
( a · b ) = 6(0) + 0(2) + 8(-5/8) = -5
2( a · b )a = 2(-5)( 6i + 8k)
2( a · b )a = - 60 i–80 k
Florencio Pinela C.

27. PROBLEMAS PROPUESTOS
PRODUCTO ESCALAR Y PRODUCTO
VECTORIAL
1. Dado los vectores A=2i + 3j + k y B=3j + 4k, la proyección del vector A sobre
el vector B es:
a) 0
b) 1
c) 13/5
d) 14
e) 5/13
2. Considere la línea que une los puntos extremos de los vectores A= 2i – j – k, B=
-i +3j – k. ¿Cuál de las siguientes alternativas es verdadera?
a) La línea es paralela al plano YZ
b) La línea es perpendicular al plano YZ
c) La longitud de la línea es 10
d) La línea es paralela al plano XY
e) Ninguna de las anteriores
3. Sean las rectas AB y AC las que se cruzan en el punto A de coordenadas (4,-5,6),
y los puntos B y C de coordenadas (2,3,5) y (5,4,2) respectivamente.¿Cuál de las
siguientes alternativas representaría un vector perpendicular al plano formado por
las rectas?.
a) –23 i – 9 j – 26 k
b) 9 i – 14 j + 8 k
c) 9 i – 23 j + 26 k
d) 23 i – 9 j + 26 k
e) –9 i + 14 j – 8 k
4. Sobre un cuerpo de masa M actúan tres fuerzas: F1 = 2i -10j + 8k (N) , F2 = 10i +2j -
3k (N) y F3 . Si el cuerpo se mueve con velocidad constante, el valor de F3 es:
a) 12i-8j+5k N
b) –2i+10j-8k N
c) –12i+8j-5k N
d) –10i-2j-3k N
e) Imposible que se mueva con velocidad constante

28. 5. Una partícula se desplaza desde el punto p1 de coordenadas (3,-2,1)m, al punto p2 de
coordenadas (10,8,7)m. Si en el punto p1 la partícula tenía una velocidad de V = 2i + 4j
m/s. El ángulo que forma la velocidad en el punto p1 y el desplazamiento de la partícula
es:
a) 27,4º
b) 34,1º
c) 56,8º
d) 65,2º
e) 71,4º
6. Para el sistema de coordenadas mostrado en la figura, determine la magnitud de la
proyección del vector 8i – 5j + 7k sobre la recta l, la cual se encuentra en el plano x-
z.
a) 4.6
b) 6.1 y
c) 8.1
d) 10.3
e) 15.1
8
x
4
z
l
7. Una partícula describe la trayectoria mostrada en la figura. El desplazamiento de la
partícula entre los puntos p1 y p2 de coordenadas (2,-3,5) y (5,6,-4) respectivamente es:
a) 3i + 9j – 9k
b) –3i –9j + 9k y
c) 3i – 3j + k p2
d) 3i + 9j – k
e) 3i + 3j – 9k
x
p1
z

29. 8. Dos vectores A y B vienen expresados por: A = 3i + 4j + k ; B = 4i - 5j + 8k. Es
verdad que A y B:
a) Son paralelos y apuntan en la misma dirección.
b) Son paralelos y apuntan en direcciones contrarias.
c) Forman un ángulo de 45º entre sí.
d) Son perpendiculares.
e) Todas las alternativas anteriores son falsas.
9. Encontrar el valor de x para que los vectores A (5, 1, -2) y B (2, x, 6) sean
perpendiculares.
a) 8
b) 6
c) 4
d) 2
e) 0
10. Sean tres vectores:
A = 3i + 2j - k
B = i - j + 2k
C=j+k
Si M = A- B y N = C x A, el ángulo formado entre los vectores M y N es
a) 60,5º
b) 41,2º
c) 51,2º
d) 68,5º
e) 72,1º
11. El vector de módulo 6 y que es perpendicular al plano formado por los vectores
A = 2 i + j -2 k y B = - 3 i - j + k es
a) 3/ 26 i + 4/ 26 j + 1/ 26 k
b) 18 / 26 i + 24/ 26 j + 6/ 26 k
c) -2/ 2 i + 8/ 2 j + 2/ 2 k
d) -6/ 2 i + 24/ 2 j + 6/ 2 k
e) 1/ 2 i + 2/ 2 j + 3/ 2 k

30. 12. Sean los vectores a, b, c, d y e, evalúe la siguiente operación
(a+c+d+e).b
a) 500 e =10 c =30
b) 799
c) 890 30º b=50
d) 1299 a =10
e) 23
d = 20
13. Sean los vectores a = 2 i – j + 2 k y b = 2 i – 3 j – k, evalúe la siguiente
operación:
(a – b ) a
a) 4
b) –4
c) 6
d) 8
e) -8
14. Sean los vectores A = 3 i – j + 2 k y B = -2 i – 2 j – 4 k, el vector unitario perpendicular al
plano formado por los vectores A y B es
a) 0 i + 8/ 128 j - 8/ 128 k
b) 8/ 192 i + 8/ 192 j - 8/ 192 k
c) –1/ 186 i - 11/ 186 j - 8/ 186 k
d) 8/ 192 i - 8/ 192 j + 8/ 192 k
e) 8/ 384 i + 16/ 384 j - 8/ 384 k
15. ¿Cuál de las siguientes alternativas representa un vector perpendicular al plano
sombreado de la figura. y
6
a) 24i + 20j + 30k
b) –5i + 6j + 8k
c) –12i – 10j + 15k 5 x
d) 12i – 10j –15k
e) 24i + 20j+ 15k 4

31. 16. Dados los vectores A, B y C siendo m un escalar, ¿cuál proposición no se
cumple?
a) A·B=B·A
b) A–B B–A
c) m(A x B) = (m A) x B
d) Ax B = B xA
e) Todas se cumplen.