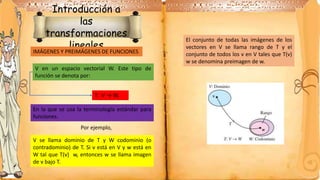
1. Introducción a
las
transformaciones
lineales
IMÁGENES Y PREIMÁGENES DE FUNCIONES
V en un espacio vectorial W. Este tipo de
función se denota por:
En la que se usa la terminología estándar para
funciones.
T: V → W.
El conjunto de todas las imágenes de los
vectores en V se llama rango de T y el
conjunto de todos los v en V tales que T(v)
w se denomina preimagen de w.
V se llama dominio de T y W codominio (o
contradominio) de T. Si v está en V y w está en
W tal que T(v) w, entonces w se llama imagen
de v bajo T.
Por ejemplo,

2. TRANSFORMACIONES
LINEALES
Definición de transformación lineal
Sean V y W espacios vectoriales. La
función
Se llama transformación lineal de V en W si
las dos propiedades siguientes son
verdaderas para todo u y v en V y para
cualquier escalar c.
𝑇: 𝑉 → 𝑊
Se dice que una transformación lineal
conserva operaciones porque se obtiene el
mismo resultado si las operaciones de suma
y multiplicación escalar se efectúan antes o
después de que se aplique la
transformación lineal. Aunque se utilizan los
mismos símbolos para denotar las
operaciones vectoriales tanto en V como en
W, debe observar que las operaciones
pueden ser diferentes, como se indica en el
siguiente diagrama.
1.- 𝑇 𝑢 + 𝑣 = 𝑇 𝑢 + 𝑇(𝑣)
2.-T c u = cT(u)

3. Propiedades de las
transformaciones lineales
Sea T una transformación lineal de V en W, donde
u y v están en V. Entonces, las propiedades
siguientes son verdaderas.
1.- 𝑇(0)
2.- 𝑇 −𝑣 = −𝑇 𝑣
3.- 𝑇 𝑢 − 𝑣 = 𝑇 𝑢 − 𝑇(𝑣)
4.- 𝐼𝑓 𝑣 = 𝑐1𝑣1 + 𝑐2𝑣2 + ⋯ + 𝑐𝑛𝑣𝑛
Entonces 𝑇 𝑣 = 𝑇(𝑐1𝑣1 + 𝑐2𝑣2 + ⋯ +
• Para demostrar la primera propiedad, observe
que 0𝑣 = 0. Entonces, se concluye que
𝑇 0 = 𝑇 0𝑣 0𝑇 𝑣 = 0
• La segunda propiedad se concluye de – 𝑣 =
(– 1)𝑣, que implica que
𝑇 −𝑣 = 𝑇 −1 𝑣 = −1 𝑇 𝑣 = −𝑇( 𝑣)
• La tercera propiedad se concluye de que
𝑢 – 𝑣 = 𝑢 (– 𝑣), que implica que
𝑇 𝑢 − 𝑣 = 𝑇 𝑢 + −1 𝑣 = 𝑇 𝑢 + −1 𝑇 𝑣
= 𝑇 𝑢 − 𝑇(𝑣)

4. La transformación lineal definida
por una matriz
Sea a una matriz de m n. La función T
definida por
es una transformación lineal de 𝑅𝑛
𝑎 𝑅𝑚
.
Para formar la multiplicación matricial con
una matriz de m n, los vectores en 𝑅𝑛 se
representan por matrices de 𝑛 𝑥 1 y los
vectores en 𝑅𝑚 se representan por matrices
de m 𝑥 1 .
𝑇 𝑣 = 𝐴𝑣
Asegúrese de comprender que una
matriz a de m n define una
transformación lineal
de 𝑅𝑛
𝑎 𝑅𝑚
.
𝐴𝑣 =
𝑎11
𝑎21
⋮
𝑎𝑚1
𝑎12 … 𝑎1𝑛
𝑎22
⋮
…
𝑎2𝑛
⋮
𝑎𝑚2 … 𝑎𝑚𝑛
𝑣1
𝑣2
⋮
𝑣𝑛
=
𝑎11𝑣1
𝑎21𝑣1
⋮
𝑎𝑚1𝑣1
+
+
.
+
𝑎12𝑣2 + ⋯ + 𝑎1𝑛𝑣𝑛
𝑎22𝑣2 + ⋯ + 𝑎2𝑛𝑣𝑛
⋮
𝑎𝑚2𝑣2
.
+ ⋯ +
⋮
𝑎𝑚𝑛𝑣𝑛
Vector
en 𝑅𝑁
Vector en 𝑅𝑀