Matemática 1, para el primer ciclo de la carrera de ingeniería.

1. LÍMITES Y CONTINUIDAD
MATEMÁTICA 1

2. lím
x  2
f(x)01. Calcular si existe, el , donde:
x3 - 2x2 - 4x + 8
x - 2|
lím
x  2
02. Halle: (x +  x2 - x3 + 1 )límx  
3
Trabajo grupal
a3 + b3 = (a + b) (a2 – ab + b2)

3. c) Tercer caso: Indeterminación  - 
01. Determine el valor de:
lím
x  2

4. 02. Halle: lím
x/2

5. 03. Calcule: (csc x - cot x)límx  0

6. d) Cuarto caso: Indeterminación 0.
01. Halle: lím
x -3

7. 02. Halle: lím
x  0
sen (3x) . csc (3x)

8. 03. Halle: lím
x  2

9. 04. Halle: lím
x/2
tg (x) . cos (x)

10. Funciones trigonométricas (F.T.)
F.T = (x; y)RR / y = RT(x)
Se denomina función trigonométrica al conjunto de
pares ordenados (x; y), tal que la primera
componente “x” es la medida de un ángulo
trigonométrico en radianes (número real) y a segunda
componente “y” es el valor de la razón
trigonométrica de x.

11. Función seno
f (x) = (x; y)RR / y = sen(x), x  R
O simplemente:
y = f (x) = sen x, xR
Dsen x = R
Rsen x = -1; 1

12. f(x) = (x; y)RR / y = cos(x), x  R
O simplemente:
y = f (x) = cos x, xR
Dcos x = R
Rcos x = -1; 1
Función coseno

13. f(x) = (x; y)RR / y = tan(x), x ≠ (2k + 1)(/2), kZ
O simplemente:
y = f (x) = tan x
Dtan x = R - (2k + 1)(/2), kZ
Rtan x = R
Función tangente

14. Líneas
trigonométricas
E(1; tg )
Q(ctg ; 1)
P(cos ; sen )

15. Líneas
trigonométricas
C(sec ; 0)
D(0; csc )

16. Resumen de las características de las
funciones trigonométricas

17. i) Si y = f (x) = c = 0
d( y)
dx
Algunas reglas de derivación
ii) Si y = f (x) = x = 1
d( y)
dx
iii) Si y = f (x) = xn
= nxn-1
d( y)
dx
iv) Si y = f (x) + g(x)
d( y)
dx

18. v)
Si y = f (x). g(x) = f (x).g’(x) + f ’(x).g(x)
d( y)
dx
vi)
Si y =
g(x). f ’(x) - f (x).g’(x)d( y)
dx
f (x)
g(x)
=
[g(x)]2
Si f (x) y g(x), son funciones derivables en x y g(x) ≠ 0,
entonces f /g es diferenciable en x.
Derivación del cociente de dos funciones
Derivación del producto de dos funciones

19. vii)
d
dx
[(f o g)(x)] = f ’[g(x)].g’(x)
=
Si la función f (x) es diferenciable en u = g(x) y la
función g es diferenciable en x, entonces la composición
y = (f o g)(x) = f [g(x)] es diferenciable en x.
Derivación de una función compuesta (Regla
de la cadena)
En forma equivalente
d(y)
dx
d(y)
du
d(u)
dx
.

20. Derivada de funciones trigonométricas
Si u = f (x) es una función derivable en x, entonces:
i) Si y = sen[f(x)]
ii)
iii)
= cos[f(x)].f’(x)]
d( y)
dx
Si y = cos[f(x)] = -sen[f(x)].f’(x)]
dx
d( y)
Si y = tan[f(x)] = sec2[f(x)].f’(x)]
dx
d( y)

21. Si u = f (x) es una función derivable en x, entonces:
iv) Si y = cot[f(x)]
v)
vi)
= -csc2[f(x)].f’(x)]
d( y)
dx
Si y = sec[f(x)] = sec[f(x)].tan[f(x)]. f’(x)]
dx
d( y)
Si y = csc[f(x)] = -csc[f(x)].cot[f(x)]. f’(x)]
dx
d( y)
Derivada de funciones trigonométricas

22. lím
x  0
sen xi).
Límites trigonométricas
x = 1
lím
x  0
tan xii).
x = 1
lím
x  0
1 - cos xiii).
x = 0
lím
x  0
1 - cos xiv).
x2
=
1
2

23. lím
x  0
sen (2x)
01. x

24. lím
x  0
1 – cos (x)
02.
sen (x)

25. lím
x  0
sen (6x)
03.
x
lím
x  0
sen (ax)
04.
sen (bx)

26. lím
x  2
sen(x - 2)
05.
3x - 6

27. lím
x  1
sen(1 - x)
06.
x - 1

28. lím
x  0
tan (x) – sen (x)
07.
x3

29. lím
x  0
6x – sen (2x)
08.
2x + 3 sen (4x)

30. lím
x  0
cos (mx) – cos (nx)
09.
x2

31. lím
x  0
1 + sen (x) – cos (x)
10.
1 - sen (x) – cos (x)

32. lím
x  0
sen (7x) - sen (3x)
11.
x.cos (x)

33. lím
x  /3
1 - 2cos (x)
12.
 - 3x

34. lím
x  0
cos (x) - cos (sen x)
13.
x2

35. lím
x  0
1 – cos sen (4x)
14.
sen2 sen (3x)

36. lím
x  /4
sen (2x) - cos (x) - 1
15.
sen (x) - cos (x)

37. lím
x  1
arc sen (x – 1/2)
16.
arc tan (x)

38. Trabajo grupal
01. Halla el límite de:
02. Calcula el límite de:

39. Límite de funciones exponenciales
a) Función exponencial
Si b > 0  b  1, entonces una función
exponencial es:
y = f(x) = bx
El dominio de una función exponencial es el
conjunto de números reales. Df = R
Rf = 0, +
El eje x, es decir, y = 0, es una asíntota
horizontal para la gráfica de f.

40. Ejemplo 1
Grafique la
función: y = f(x)
= 2x.
0
0.5
1
1.5
2
2.5
3
3.5
4
4.5
5
5.5
6
6.5
7
7.5
8
8.5
-2 -1.5 -1 -0.5 0 0.5 1 1.5 2 2.5 3 3.5
Gráfico de la función exponencial f(x) = 2x
Cuando la base b > 1
límx  -
bx
= 0
límx  +
bx
= +
Asíntota horizontal

41. Ejemplo 2
Grafique la
función: y = f(x)
= (1/2)x.
Cuando la base
0 < b < 1
límx  -
bx
= +
límx  +
bx
= 0
0
0.5
1
1.5
2
2.5
3
3.5
4
-2 -1 0 1 2 3 4
Gráfico de la función exponencial f(x) = (1/2)x
Asíntota horizontal

42. b) Función logarítmica
La función logarítmica con base b > 0  b 
1, se define por:
y = logb(x), si y sólo si, x = by
Dominio: Df = 0; + Rango: Rf = R
El eje y, es decir, x = 0, es una asíntota
vertical para la gráfica de f.
La función f es uno a uno.

43. Utilizando la propiedad principal,
y = logb(x), si y sólo si, x = by
y = logb(x) = logb(by)
x = blogb(x)
se infieren:
2 = 10log2(10)

44. c) Logaritmo natural
Es el logaritmo con base e > 0  e  1, y se
define como:
y = ln(x), si y sólo si, x = ey
Además:
ln(1) = 0, si y sólo si, e0 = 1
ln(e) = 1, si y sólo si, e1 = e

45. Gráfica de y = f(x) = log2(x)
-3.5
-3
-2.5
-2
-1.5
-1
-0.5
0
0.5
1
1.5
2
2.5
3
3.5
0 1 2 3 4 5 6 7 8 9
Gráfico de la función logarítmica f(x) = log2x
Cuando la base
b > 1
límx  + logb(x) = +
límx  0 = -logb(x)
Asíntotavertical

46. d) El número e
Ideado por John Napier en 1618 y
popularizado por Leonard Euler (1736).
e también es límite de la sucesión:
Haciendo: h = 1/x, si x tiende , h tiende a 0.

47. e) Cálculo de los límites de la forma:
f) Para funciones logarítmicas:

48. Calcula los siguientes límites:
01)

49. 02)

50. 03)

51. 04)

52. 05)

53. 06)

54. 07)

55. 08)

56. 09)

57. Derivada de funciones exponenciales y logarítmicas
i) Si y = e f(x) = e f(x) . f ’(x)
d( y)
dx
ii) Si y = ln[ f(x)]
f ’(x)d( y)
dx f (x)
=
iii) Si y = ax
d( y)
dx
ax.ln(a)=
iv) Si y = a f(x)
d( y)
dx
a f(x). f ’(x).ln(a)=

58. Casos especiales de funciones exponenciales y logarítmicas
i) ln(ex) = x ii) eln(x) = x
1
x1 +( )
x
lím
x  +∞
= eiii)
1 + x( )
1/x
lím
x  0
= eiv)

x1 +( )
x
lím
x  +∞
= ev)

59. Casos especiales de funciones exponenciales y logarítmicas
ax - 1
x( )lím
x  0
= ln(a)vi) Si a >1  a 1
ex - 1
x( )lím
x  0
= 1vii)

60. 10) 7x - 1
x
lím
x  0
( )

61. 11) 7x - 5x
x
lím
x  0
( )

62. 12) 9x - 7x
lím
x  0
( )8x - 6x

63. 13) ex - ex
lím
x  0
( )x

64. 14) ex - ex
lím
x  0 ( )sen x – sen x

65. 15) sen 2xlím
x  0 ( )ln (1 + x)

66. 16) lím
x  /2 (1 + cos x)3.sec x

67. 17) lím
x  0
(1 + 3.tan2 x)
cot2 x

68. 18)

69. 01)
Trabajo grupal
02)

70. Asíntotas de una función
a) Si una recta L y un punto A que se desplaza a lo
largo de la curva C: y = f(x), la distancia entre la
recta L y el punto A de la curva tiende a cero,
cuando el punto A tiende al infinito; en este caso, la
recta L se denomina asíntota de la curva C.

71. b) La recta x = a, es una asíntota vertical de la
curva C: y = f(x), si se cumple una de las
siguientes relaciones:
i) lím
x  a
f(x) = ±∞
ii) lím
x  a+
f(x) = ±∞
iii) lím
x  a-
f(x) = ±∞
-∞
+∞

72. c) La recta y = k, es una asíntota horizontal de
la curva C: y = f(x), si se cumple una de las
siguientes relaciones:
i) lím
x  +∞
f(x) = k
ii) lím
x  -∞
f(x) = k
iii) lím
x  ∞
f(x) = k
Asíntota horizontal

73. d) La recta y = mx + b, es una asíntota oblicua
de la curva C: y = f(x), si se cumple que:
i) lím
x  +∞
[f(x) – (mx + b)] = 0
ii) lím
x  -∞
[f(x) – (mx + b)] = 0
Formas de encontrar los valores de “m” y “b”.
f(x)lím
x  ±∞( )xm =
[f(x) – mx]lím
x  ±∞b =

74. 01. Halla las asíntota de la función:
x2 + x - 1
x - 3y = f(x) =

75. -50
-45
-40
-35
-30
-25
-20
-15
-10
-5
0
5
10
15
20
25
30
35
40
45
50
55
-6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 9 10 11 12
Gráfico de la función: y = (x2 + x -1)/(x - 3)
Curva Asíntota oblicua
Asíntotavertical
Asíntota vertical:
x = 3
Asíntota oblicua:
y = x + 4
Asíntota horizontal:
No existe

76. 02. Halla las asíntota de la función:
2x2 – 5x + 3
x - 1y = f(x) =

77. 03. Halla las asíntota de la función:
2x2 + 5x - 8
x + 3y = f(x) =

78. 04. Halla las asíntota de la función:
x2 + 2x - 8
x2 - 4y = f(x) =
-8
-7
-6
-5
-4
-3
-2
-1
0
1
2
3
4
5
6
7
8
9
10
-12 -10 -8 -6 -4 -2 0 2 4 6 8
Gráfico

79. 05. Halla las asíntota de la función:
x + 3
x + 2
y = f(x) =

80. 06. Halla las asíntota de la función:
6x2 + 8x - 3
3x2 + 2
y = f(x) =
-3
-2
-1
0
1
2
3
-9 -8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 9
Gráfica de la función
Asíntota horizontal

81. 01.
Halla las asíntotas de las funciones y
representa gráficamente:
Trabajo grupal
x2
2 - x
y = f(x) =
02.
2x2
x + 3
y = f(x) =

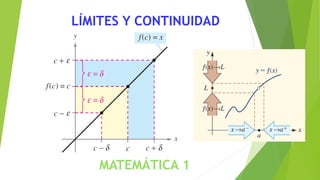
82. Una función real f es continua en un
número x = a si:
Continuidad de una función
lím
x  a
f(x) = f(a)
Si f es continua en a, entonces debe cumplir:
i) f (a) esta definida (esto es, a pertenece al dominio de f )
ii) lím
x  a
f(x) Existe
iii) lím
x  a
f(x) = f(a)

83. Si f es continua, entonces los puntos (x, f (x)) en la
gráfica de f tienden al punto (a, f (a)) sobre la gráfica.
Así que no existe ninguna brecha en la curva

84. Discontinuidad evitable o removible.
Tipos de discontinuidad
lím
x  a
f(x)i)
Una función real de variable real f: R  R,
tiene una discontinuidad evitable y removible en
un punto x = a, si:
a)
Existe
ii) El número aDf, o bien aDf se tiene que:
lím
x  a f(x) ≠ f(a), en este caso redefinimos f:
F(x) =
f(x), si x ≠ a
x  a
f(x), si x = a
lím


85. Discontinuidad no evitable o removible.
i) Discontinuidad de primera especie una
función real es discontinua cuando tiene
límites laterales son infinitos y diferentes.
b)
ii) Discontinuidad de segunda especie de una
función real es discontinuidad en el punto x
= a, si no existe , o si, uno de los
límites laterales es infinito (±∞)
x  a
lím f(x)

86. Ejemplos:
¿Dónde es discontinua cada una de las
siguientes funciones?
a)
x2 – x - 2
x - 2
f(x) =
1)

87. b)
1
x2
f(x) =
1, si x = 0
, si x ≠ 0


88. c)
x2 – x - 2
x - 2
f(x) =
1, si x = 2
, si x ≠ 2


89. Determina los valores de x para los cuales la
función f es discontinua y evitar si es posible
redefiniendo la función.
x4 – 81
x2 - 9
f(x) =
2)

90. Determina los valores de x para los cuales la
función f es discontinua y evitar si es posible
redefiniendo la función.
x3 – 2x2 – 11x + 12
x2 – 5x + 4
f(x) =
3)

91. Determina los valores de x para los cuales la
función f es discontinua y evitar si es posible
redefiniendo la función.
3x3 + 2x2 – 6x + 1
x2 – x
f(x) =
4)

92. x3 - x2 + 2x - 2
x – 1f(x) =
5) , para x ≠ 1
4, para x = 1

93. 3x2 - 7x + 2
x – 2f(x) =
6) , para x ≠ 0
3, para x = 0