Problemario de Series de Fourier
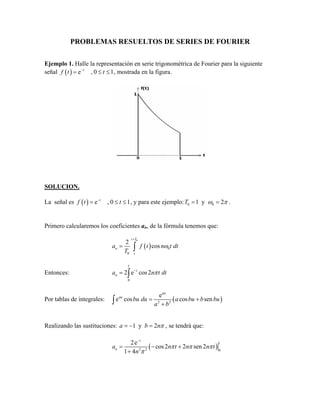
- 1. PROBLEMAS RESUELTOS DE SERIES DE FOURIER Ejemplo 1. Halle la representación en serie trigonométrica de Fourier para la siguiente señal ( ) e , 0 1t f t t− = ≤ ≤ , mostrada en la figura. SOLUCION. La señal es ( ) e , 0 1t f t t− = ≤ ≤ , y para este ejemplo: 0 01 y 2T ω π= = . Primero calcularemos los coeficientes an, de la fórmula tenemos que: ( ) 0 0 0 2 cos t T n t a f t n t dt T ω + = ∫ Entonces: 1 0 2 e cos2t na n t dtπ− = ∫ Por tablas de integrales: ( )2 2 e e cos cos sen au au bu du a bu b bu a b = + +∫ Realizando las sustituciones: 1 y 2a b nπ= − = , se tendrá que: ( ) 1 2 2 0 2e cos2 2 sen 2 1 4 t na n t n n t n π π π π − = − + +
- 2. Evaluando límites: 1 2 2 2 e cos2 1 4 na n n π π − = − + 1 2 sen 2n nπ π = +( )0 0 e cos(0) = − − 1 2 sen(0)nπ = +( )0= ⎡ ⎤ ⎢ ⎥⎣ ⎦ De tal forma que: ( )1 2 2 2 1 e . 1 4 na n n π − = − ∀ + Ahora calcularemos el coeficiente independiente a0. A partir de la fórmula: ( ) 0 0 0 1 1 1 0 0 0 0 1 e e e e t T t t t a f t dt T a dt + − − − = = = − = − + ∫ ∫ ⇒ 1 0 1 e 1.264a − = − ≅ Concluimos calculando los coeficientes bn: ( ) 0 0 0 2 sen t T n t b f t n t dt T ω + = ∫ Por tablas de integrales: ( )2 2 e e sen sen cos au au bu du a bu b bu a b = − +∫ Sustituyendo 1 y 2a b nπ= − = , se tendrá entonces: ( ) 1 2 2 0 2e sen 2 2 cos2 1 4 t nb n t n n t n π π π π − = − − + 1 2 2 2 e sen 2 1 4 nb n n π π − = − + 0 2 cos2n nπ π = −( )1 0 e sen(0) = − − 0 2 cos(0)nπ = −( )1= ⎡ ⎤ ⎢ ⎥⎣ ⎦ 1 2 2 2 2 e 2 1 4 nb n n n π π π − ⎡ ⎤= − +⎣ ⎦+ ⇒ ( )1 2 2 4 1 e . 1 4 n n b n n π π − = − ∀ +
- 3. Finalmente, la representación en serie trigonométrica de Fourier para la señal ( )f t será: ( ) ( ) ( )1 1 2 2 2 2 1 2 4 1.264 1 e cos2 1 e sen 2 1 4 1 4n n f t n t n t n n π π π π π ∞ − − = ⎡ ⎤ ≅ + − + −⎢ ⎥+ +⎣ ⎦ ∑
- 4. Ejemplo 2. Halle la representación en serie trigonométrica de Fourier para la siguiente señal ( ) 2 , 0 1f t t t= ≤ ≤ , mostrada en la figura. SOLUCION. La señal es ( ) 2 , 0 1f t t t= ≤ ≤ , y para este ejemplo: 0 01 y 2T ω π= = . Primero calcularemos los coeficientes an. De la fórmula tenemos que: ( ) 0 0 0 2 cos t T n t a f t n t dt T ω + = ∫ 1 2 0 2 cos2na t n t dtπ= ∫ Utilizando integración por partes: 2 2 1 cos2 sen 2 2 u t du t dt dv n t dt v n t n π π π = ⇒ = = ⇒ = 1 1 2 0 0 1 2 2 sen 2 sen 2 2 2 na t n t t n t dt n n π π π π ⎡ ⎤ = −⎢ ⎥ ⎢ ⎥⎣ ⎦ ∫ 1 1 1 2 0 0 0 1 2 1 1 sen 2 cos2 cos2 2 2 na t n t t n t n t dt n n n n π π π π π π π ⎡ ⎤ = − − +⎢ ⎥ ⎢ ⎥⎣ ⎦ ∫ 1 1 1 2 2 2 0 0 0 1 2 1 1 sen 2 cos2 sen 2 2 4 na t n t t n t n t n n n n π π π π π π π ⎡ ⎤ = − − +⎢ ⎥ ⎢ ⎥⎣ ⎦ 1 1 1 2 2 2 3 3 0 0 0 1 1 1 sen 2 cos2 sen 2 2 na t n t t n t n t n n n π π π π π π = + −
- 5. ( ) 21 1 sen 2na n n π π = ( ) 0 2 2 1 0 1 cos2n n π π = ⎡ ⎤− +⎢ ⎥⎣ ⎦ 1 3 3 0 1 sen 2 2 n n π π = ⎡ ⎤−⎢ ⎥⎣ ⎦ − ( ) 0 sen 0 = − 0= ⎡ ⎤ ⎢ ⎥⎣ ⎦ ⇒ 2 2 1 0.na n n π = ∀ ≠ Calculando el coeficiente 0a : ( ) 0 0 0 1 t T t a f t dt T + = ∫ ( ) 1 12 3 0 0 0 1 1 1 0 3 3 a t dt t= = = −∫ ⇒ 0 1 3 a = Calculando el coeficiente bn: ( ) 0 0 0 2 sen t T n t b f t n t dt T ω + = ∫ 1 2 0 2 sen 2nb t n t dtπ= ∫ Aplicando integración por partes: 2 2 1 sen 2 cos2 2 u t du t dt dv n t dt v n t n π π π = ⇒ = = ⇒ = − 1 1 2 0 0 1 1 2 cos2 2 cos2 2 2 nb t n t t n t dt n n π π π π ⎡ ⎤ = − +⎢ ⎥ ⎢ ⎥⎣ ⎦ ∫
- 6. 1 1 2 0 0 1 2 cos2 cos2nb t n t t n t dt n n π π π π = − + ∫ Volviendo aplicar integración por partes: 1 cos2 sen 2 2 u t du t dt dv n t dt v n t n π π π = ⇒ = = ⇒ = Realizando las operaciones correspondientes: 1 1 1 2 0 0 0 1 2 1 1 cos2 sen 2 sen 2 2 2 nb t n t t n t n t dt n n n n π π π π π π π ⎡ ⎤ = − + −⎢ ⎥ ⎢ ⎥⎣ ⎦ ∫ 1 1 1 2 0 0 0 1 2 1 1 1 cos2 sen 2 cos2 2 2 2 nb t n t t n t n t n n n n n π π π π π π π π ⎡ ⎤ = − + + ⋅⎢ ⎥ ⎢ ⎥⎣ ⎦ 1 1 1 2 2 2 3 3 0 0 0 1 1 1 cos2 sen 2 cos2 2 nb t n t t n t n t n n n π π π π π π = − + + 1 cos2nb n n π π = − 1 2 2 1 0 sen 2n n π π = ⎡ ⎤− +⎢ ⎥⎣ ⎦ 0 3 3 0 1 cos2 2 n n π π = ⎡ ⎤− +⎢ ⎥⎣ ⎦ ( ) 1 cos 0 = − 1= ⎡ ⎤ ⎢ ⎥⎣ ⎦ ⇒ 1 .nb n nπ = − ∀ Finalmente, la serie de Fourier para la señal ( )f t es: ( ) 2 2 1 1 1 1 cos2 sen 2 3 n f t n t n t n n π π π π ∞ = ⎡ ⎤ = + −⎢ ⎥⎣ ⎦ ∑
- 7. Ejemplo 3. Halle la representación en serie trigonométrica de Fourier para la siguiente señal, mostrada en la figura. Suponga que el intervalo de repetición para la serie será de −π a +π. SOLUCION. La señal ( )f t se definirá como: ( ) 2 2cos , 0 , A t t f t otro caso π π − ≤ ≤⎧ = ⎨ ⎩ Para la serie de Fourier tendremos que: 0 02 y 1T π ω= = . Dado que la señal ( )f t tiene simetría par, entonces los coeficientes 0nb = . Para este caso, solo consideraremos el cálculo de los coeficientes an. Por definición: ( ) 0 0 0 2 cos t T n t a f t n t dt T ω + = ∫ Sustituyendo: 2 2 2 2 2 cos cos cos cos 2 n A a A t nt dt t nt dt π π π ππ π + + − − = =∫ ∫ Resolviendo la integral por tablas: ( ) ( ) ( ) ( ) sen sen cos cos 2 2 a b u a b u au bu du a b a b − + = + − +∫ Sustituyendo 1 ya b n= = , en la integral: ( ) ( ) ( ) ( ) 2 2 2 2 sen 1 sen 1 2 1 2 1 n n t n tA a n n π π π π π + + − − ⎡ ⎤− + ⎢ ⎥= + − +⎢ ⎥ ⎣ ⎦
- 8. Evaluando los límites: ( )( ) ( )( ) ( ) ( )( ) ( )( ) ( ) 2 2 2 2sen 1 sen 1 sen 1 sen 1 2 1 2 1 n n n n nA a n n π π π π π ⎡ ⎤− − − − + − + − = +⎢ ⎥ − +⎣ ⎦ ( )( ) ( )( ) ( ) ( )( ) ( )( ) ( ) 2 2 2 2sen 1 sen 1 sen 1 sen 1 2 1 2 1 n n n n nA a n n π π π π π ⎡ ⎤− + − + + + = +⎢ ⎥ − +⎣ ⎦ ( )( ) ( )( )2 2sen 1 sen 1 1 1 n n nA a n n π π π ⎡ ⎤− + = +⎢ ⎥ − +⎣ ⎦ Por identidades trigonométricas: ( )sen 1 sen sen 2 2 2 2 n n π π π π⎛ ⎞ ⎛ ⎞ ± = ± =⎜ ⎟ ⎜ ⎟ ⎝ ⎠ ⎝ ⎠ 1 cos cos 2 2 nπ π = ± 0 sen cos 2 2 n nπ π = = Entonces: 2 2cos cos 1 1 cos 1 1 2 1 1 n n n A A n a n n n n π π π π π ⎛ ⎞ ⎛ ⎞⎛ ⎞ = + = +⎜ ⎟⎜ ⎟⎜ ⎟− + − +⎝ ⎠⎝ ⎠⎝ ⎠ ( )( ) 1 1 cos 2 1 1 n A n n n a n n π π ⎛ ⎞+ + −⎛ ⎞ = ⎜ ⎟⎜ ⎟⎜ ⎟− +⎝ ⎠⎝ ⎠ ⇒ ( )2 2 cos 1. 21 n A n a n n π π = ∀ ≠ − De la expresión anterior obtenida para los coeficientes an, se establece que esta expresión es válida para toda n excepto para 1n = , dado que para ese valor se produce una indeterminación. Se procede a obtener dicho valor a1, el cual puede obtenerse sustituyendo el valor particular de n, para este caso 1n = , en la expresión general de los coeficientes an, antes de proceder al cálculo integral, tal como se muestra a continuación: Formula general: ( ) 0 0 0 2 cos t T n t a f t n t dt T ω + = ∫ Para el caso 1n = : 2 2 2 1 cos A a t dt π ππ + − = ∫
- 9. Por identidad trigonométrica: ( )2 1 cos 1 cos2 2 t t= + Entonces: ( ) 2 2 2 2 2 2 1 1 1 cos2 cos2 2 2 A A a t dt dt t dt π π π π π ππ π + + + − − − ⎛ ⎞ ⎜ ⎟= + = + ⎜ ⎟ ⎝ ⎠ ∫ ∫ ∫ ( )22 2 2 1 1 2 sen 2 2 A a t t ππ π π π ++ − − = + Evaluando límites: 1 1 sen 2 2 2 2 A a π π π π ⎛ ⎞ = + +⎜ ⎟ ⎝ ⎠ 0 senπ = +( )0=⎡ ⎤ ⎢ ⎥ ⎣ ⎦ 1 2 A a⇒ = Si recordamos el concepto de cálculo diferencial sobre la regla de L’Hopital, ésta se utiliza para encontrar el límite de una función en un punto, cuando en ese punto la función presentara una indeterminación. Si aplicamos esta regla a la expresión obtenida para los coeficientes an, tendremos lo siguiente: Expresión general: ( )2 2 cos 21 n A n a n π π = − Aplicando regla L’Hopital: ( ) ( ) ( ) 1 1 1 1 2 1 1 2 cos 2 sen 2 2 2 lim 2 1 n n n n n n d n n A A dx a a d n n dx π π π π π = = → = = ⎡ ⎤ ⎛ ⎞ −⎜ ⎟⎢ ⎥⎣ ⎦ ⎝ ⎠ = = = −⎡ ⎤−⎣ ⎦ Evaluando: 1 sen 2 A a π π− = 1 2 2 A π = = − De lo anterior, se deduce que a consideración del estudiante, tiene 2 opciones para encontrar el valor particular de aquel coeficiente an (y de igual manera para cualquier coeficiente bn) donde 0n ≠ , produzca una indeterminación en la expresión general. Ahora, solo basta hallar el coeficiente independiente a0. Según la fórmula: ( ) 0 0 0 1 t T t a f t dt T + = ∫
- 10. ( ) 2 2 22 0 2 1 cos sen sen 2 2 2 A A a A t dt t π π ππ π π π π + + −− = = =∫ ( ) 1 2sen π = − − 1=− ⎡ ⎤ ⎢ ⎥⎣ ⎦ ⇒ 0 A a π = Luego entonces, la serie de Fourier para esta señal será: ( ) ( )2 2 2 cos cos cos 2 21n A A A n f t t nt n π π π ∞ = = + + − ∑
- 11. PROBLEMAS PROPUESTOS DE SERIES DE FOURIER Encuentre las representaciones en serie trigonométrica de Fourier para las señales mostradas a continuación. 10 -10 2 -2 f(t) t 4 -4 1 -1 g(t) t 5 0.1-0.1 y(t) t ...... 0.2-0.2 1 h(t) t ...... Función generatriz: cos(at) π 4 π 4 π 2 π 2 RESPUESTAS. (a) 10 , 2 0 ( ) 10 , 0 2 t f t t − ≤ ≤⎧ = ⎨ − ≤ ≤⎩ Como ( )f t es impar 0na⇒ = . ( ) 220 1 cos 10 Sa 2 n n b n n n π π π π ⎡ ⎤ = − − = − ⎢ ⎥⎣ ⎦ 2 1 ( ) 10 Sa sen 2 2n n n t f t n π π∞ = ⎡ ⎤ = − ⎢ ⎥⎣ ⎦ ∑
- 12. (b) ( ) ( ) 4 1 , 1 0 ( ) 4 1 , 0 1 t t g t t t + − ≤ ≤⎧⎪ = ⎨ − ≤ ≤⎪⎩ Como ( )f t es impar 0na⇒ = . 8 nb nπ = − ( ) 1 8 ( ) sen n g t n n tπ π ∞ = = − ∑ (c) 1 10 1 10 5sen10 , 0 ( ) ( ) t t y t y t π ≤ ≤⎧ = ⎨ ±⎩ Como ( )f t es par 0nb⇒ = . ( )2 20 1 4 na n nπ = ∀ − y 0 10 a π = ( ) ( )2 1 10 20 ( ) cos 20 1 4n y t nt n π π π ∞ = = + − ∑ (d) 4 4 2 cos2 , 0 ( ) 0 , t t h t t π π π ≤ ≤⎧ = ⎨ ≤ ≤⎩ ( )2 2cos 1 4 n n a n n π π = ∀ − y 0 1 a π = ( )2 4 1 4 n n b n nπ − = ∀ − ( ) ( ) ( ) ( )2 2 1 1 2cos 4 ( ) cos 4 sen 4 1 4 1 4n n n h t nt nt n n π π π π ∞ = ⎡ ⎤ ⎢ ⎥= + − − −⎢ ⎥⎣ ⎦ ∑
