operaciones con funciones

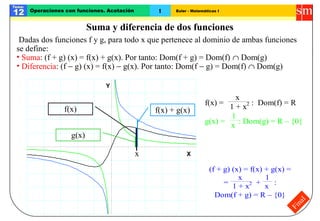
1. Euler - Matemáticas I
Tema:
12 1Operaciones con funciones. Acotación
Final
Suma y diferencia de dos funciones
Dadas dos funciones f y g, para todo x que pertenece al dominio de ambas funciones
se define:
• Suma: (f + g) (x) = f(x) + g(x). Por tanto: Dom(f + g) = Dom(f) ∩ Dom(g)
• Diferencia: (f − g) (x) = f(x) − g(x). Por tanto: Dom(f − g) = Dom(f) ∩ Dom(g)
-5
-4
-3
-2
-1
0
1
2
3
4
5
-5 -4 -3 -2 -1 0 1 2 3 4 5
X
Y
x
f(x) f(x) + g(x)
f(x) =
x
1 + x2 : Dom(f) = R
g(x) =
1
x
: Dom(g) = R – {0}
(f + g) (x) = f(x) + g(x) =
=
x
1 + x2 +
1
x
:
Dom(f + g) = R – {0}
g(x)
1

2. Euler - Matemáticas I
Tema:
12 2Operaciones con funciones. Acotación
Final
Función opuesta
Si f es una función, se define su función opuesta -f de la siguiente forma: (-f)(x) = -
f(x) siendo el dominio de -f el mismo que el de f
-4
-3
-2
-1
0
1
2
3
4
-1 0 1 2 3 4 5
X
Y
y = f(x)
-4
-3
-2
-1
0
1
2
3
4
-1 0 1 2 3 4 5
X
Y
y =- f(x)
Dom (f) Dom (-f)
(x, f(x))
•
•
(x, -f(x))
2

3. Euler - Matemáticas I
Tema:
12 3Operaciones con funciones. Acotación
Final
Valor absoluto de una función
Si f es una función, se define el valor absoluto de f, |f|, como: |f|(x) = |f(x)|, para
todo x que pertenece al dominio de f.
|f|(x)= |f(x)| =


f(x) si f(x) ≥0
−f(x) si f(x) < 0
=



f(x) si f(x) > 0
−f(x) si f(x) ≤0
-5
-4
-3
-2
-1
0
1
2
3
4
5
-5 -4 -3 -2 -1 0 1 2 3 4 5
X
Y
y = f(x)
puntos con
imagen negativa
Simetrizamos las partes
negativas respecto al eje OX
-5
-4
-3
-2
-1
0
1
2
3
4
5
-5 -4 -3 -2 -1 0 1 2 3 4 5
X
Y
y = |f(x)|
Conocida la gráfica de y = f(x), ¿cómo construir la gráfica de y = |f(x)|?
3

4. Euler - Matemáticas I
Tema:
12 4Operaciones con funciones. Acotación
Final
Producto y cociente de dos funciones
Dadas dos funciones f y g, para todo x que pertenece al dominio de ambas
funciones se define:
• Producto: (f . g) (x) = f(x) . g(x).
•Por tanto: Dom(f . g) = Dom(f) ∩ Dom(g)
Dadas dos funciones f y g, para todo x que pertenece al dominio de ambas
funciones y g(x) ≠ 0 se define:
• Cociente: (f / g) (x) = f(x) / g(x). Por tanto:
• Dom(f / g) = Dom(f) ∩ Dom(g) − {x ∈ R : g(x) ≠ 0}
4

5. Euler - Matemáticas I
Tema:
12 5Operaciones con funciones. Acotación
Rec(g)
Final
Composición de funciones
La función h(x) = (2x - 1)2
es la composición de dos funciones: g(x) = 2x-1 y f(t) = t2
x 2x-1 = t t2
= (2x-1)2
R R
g
R
f
x (2x-1)2
h(x) = f(g(x)) = f(2x-1) = (2x - 1)2
= (f o g)(x)
R R R
Dom(g)
Rec(f)
g f
Dominio de la composición de funciones
El dominio de fog está formado
por los x tales que
• x está en el dominio de g
• g(x) está en el dominio de f
Dom(f)
Dom(fog)
Rec(fog)
5

6. Euler - Matemáticas I
Tema:
12 6Operaciones con funciones. Acotación
Final
Funciones inyectivas
Un función f tiene la propiedad de la recta horizontal en un dominio D, si para todo
valor c del recorrido de la función, la recta y = c corta a la gráfica de f en un solo
punto.
-5
-4
-3
-2
-1
0
1
2
3
4
5
-5 -4 -3 -2 -1 0 1 2 3 4 5
X
Y
-4
-3
-2
-1
0
1
2
3
4
-1 0 1 2 3 4 5
X
Y
•• •
f no tiene la propiedad de
la
recta horizontal
f tiene la propiedad de la
recta horizontal
Formulación algebraica de la propiedad de la recta horizontal: una función
f es inyectiva en D si para a,b ∈ D tal que f(a) = f(b) se tiene que a = b
6

7. Euler - Matemáticas I
Tema:
12 7Operaciones con funciones. Acotación
Final
Función inversa
Si f inyectiva, la función inversa f, escrita f -1
, satisface x = f -1
(y) ⇔ y = f(x)
Como consecuencia:
• El dominio de f es el recorrido de f -1
• El recorrido de f -1
es el dominio de f
• Si (x, y) está sobre la gráfica de y = f(x), (x, y) está sobre la gráfica de f -1
. Por
tanto las gráficas de ambas funciones son simétricas respecto a la bisectriz del
primer cuadrante.
X
Y
X
Y
f(x)
f(x)f -1
(x)
f -1
(x)
• (x, f(x))
• (f(x), x)
• (x, f(x))
• (f(x), x)

8. Euler - Matemáticas I
Tema:
12 8Operaciones con funciones. Acotación
Final
Funciones acotadas
-5
-4
-3
-2
-1
0
1
2
3
4
5
-5 -4 -3 -2 -1 0 1 2 3 4 5
X
Y
• Una función y = f(x) está acotada superiormente (inferiormente) en un conjunto D
si existe un número M (m) tal que f(x) ≤ M (m ≤ f(x)) para todo x de D. Se dice
que M (m) es una cota superior (inferior).
• Una función acotada superior e inferiormente se dice que está acotada
M' es cota superior de f(x) en D = R
y = f(x)
y = g(x)
El supremo S, es la menor de las cotas superiores
M'' es cota superior de f(x) en D = R
m' es cota inferior de f(x) en D = R
m'' es cota inferior de f(x) en D = R
El ínfimo I, es la mayor de las cotas inferiores
• y = f(x) está acotada
• y = g(x) no está acotada
S
I
8

9. Euler - Matemáticas I
Tema:
12 9Operaciones con funciones. Acotación
X
Y
X
Y
Final
Crecimiento y decrecimiento de una función
[
a
]
b
x
f(x)
y
f(y)
Función creciente en [a, b]
f(x) < f(y) para todo x e y de [a, b]
[
a
]
b
x
f(x)
Función decreciente en [a, b]
f(x) < f(y) para todo x e y de [a, b]
f(y)
y
9

10. Euler - Matemáticas I
Tema:
12 10Operaciones con funciones. Acotación
X
Y
Final
Máximo y mínimo de una función
Mínimo, de valor T
en el punto t, de
f(x) en el conjunto
D
Máximo, de
valor S en el punto s,
de f(x) en el conjunto D
D
•
s
S
t
T•
• El máximo de una función f en D es el mayor de los valores que toma f en D.
• El mínimo de una función f en D es el menor de los valores que toma f en D.
10