AREA E INTEGRAL DEFINIDA.pdf
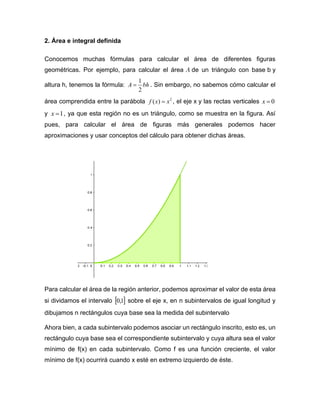
- 1. 2. Área e integral definida Conocemos muchas fórmulas para calcular el área de diferentes figuras geométricas. Por ejemplo, para calcular el área de un triángulo con base b y altura h, tenemos la fórmula: 1 2 A bh = . Sin embargo, no sabemos cómo calcular el área comprendida entre la parábola 2 ( ) f x x = , el eje x y las rectas verticales 0 x = y 1 x = , ya que esta región no es un triángulo, como se muestra en la figura. Así pues, para calcular el área de figuras más generales podemos hacer aproximaciones y usar conceptos del cálculo para obtener dichas áreas. Para calcular el área de la región anterior, podemos aproximar el valor de esta área si dividamos el intervalo 1 , 0 sobre el eje x, en n subintervalos de igual longitud y dibujamos n rectángulos cuya base sea la medida del subintervalo Ahora bien, a cada subintervalo podemos asociar un rectángulo inscrito, esto es, un rectángulo cuya base sea el correspondiente subintervalo y cuya altura sea el valor mínimo de f(x) en cada subintervalo. Como f es una función creciente, el valor mínimo de f(x) ocurrirá cuando x esté en extremo izquierdo de éste.
- 2. A continuación, calcularemos aproximaciones cada vez mejores, tomando cada vez más y más rectángulos. Observa las siguientes gráficas: En este caso, el área aproximada será un poco menor al área bajo la parábola, pero observamos que a medida que n crece la suma se aproxima al área buscada. Para este caso, vemos que se aproxima a 0.32…
- 3. Es posible, asociar a cada subintervalo un rectángulo circunscrito, esto es, un rectángulo cuya base sea el correspondiente subintervalo y cuya altura sea el valor máximo de f(x) en cada subintervalo. Como f es una función creciente, el valor máximo de f(x) ocurrirá cuando x esté en extremo derecho de éste. A continuación, calcularemos aproximaciones cada vez mejores, tomando cada vez más y más rectángulos. Observa las siguientes gráficas:
- 4. En esta circunstancia, el área aproximada será mayor al área bajo la parábola, pero observamos que a medida que n crece la suma se aproxima al área buscada. En particular, observamos que se aproxima a 0.35… Si tomamos esta información, el área de los rectángulos que quedan por encima de la parábola y de los que quedan por debajo, y los ordenamos en una tabla, tenemos: n 5 10 20 30 ÁREA 0.333 Ainf 0.24 0.29 0.31 0.32 Asup 0.44 0.38 0.36 0.35 De la tabla se hace evidente que el área tiende a un número que satisface: 0.32 0.35 A Se concluye, que la suma inferior Ainf es menor o igual que la suma superior Asup. Además, el área real de la región se encuentra entre estas dos sumas. inf sup A Área de la región A
- 5. Es notorio, que si dibujamos más rectángulos obtendremos una mejor aproximación. Entonces, si encontramos el límite de la suma de las áreas de todos los rectángulos que dibujamos bajo la curva, cuando el número de rectángulos tiende a infinito, debemos obtener el área bajo la curva ( ) y f x = desde x a = hasta x b = . Así pues, el área buscada la podemos expresar como: 1 lim ( ) n i n i b a A f x n → = − = donde la altura del rectángulo es ( ) i f x y su base b a x n − = , dado que se tienen n particiones, todas del mismo tamaño. El intervalo , a b se divide en n subintervalos de ancho b a x n − = . Definición de área bajo una curva Para una función f definida en el intervalo b a, , si f es continua y no negativa en b a, , el área A bajo la curva ( ) f x en el intervalo [a, b] está dada por: 1 lim ( ) n i n i A f x x → = = donde b a x n − = .
- 6. . Esta definición vale para cualquier función, no sólo para funciones no negativas; por tanto, se debe tener cuidado cuando se use esta definición para calcular áreas. Definición de integral definida Dada la función f , definida en un intervalo cerrado b a, . Entonces la integral definida de ( ) f x desde x a = hasta x b = , denotada por b a dx x f ) ( está dada por: 1 ( ) lim ( ) b n i x i a f x dx f x x → = = La Integral definida como área de una región. Si f continua y no negativa en el intervalo cerrado b a, , entonces el área de la región acotada por la gráfica de f , el eje x y las rectas x a = y x b = está dado por: ( ) b a Área f x dx =
- 7. • Si f(x) es no negativa en un intervalo [a, b], entonces Área = b a dx x f ) ( • Si f(x) es negativa en un intervalo [a, b], entonces Área = - b a dx x f ) ( Si en el intervalo [a, b] hay partes en que la función es negativa y partes en que no lo es, se debe calcular por separado la integral definida, en cada una estas secciones o intervalos. 2.1 Teorema fundamental del cálculo Se han visto ya dos de las principales ramas del cálculo: el cálculo diferencial (presentado con el problema de la recta tangente) y el cálculo integral (presentado con el problema del área). En este punto, podría parecer que estos dos problemas no se relacionan, aunque tienen una conexión muy estrecha. La conexión fue Propiedades de la integral definida La definición de la integral definida de f en el intervalo [a, b] especifica que a < b, sin embargo, es posible extender esta definición para los casos donde a = b o donde a > b. i) Si f está definida en x a = , entonces se define ( ) 0 a a f x dx = ii) Si f es integrable en b a, , entonces se define ( ) ( ) b a a b f x dx f x dx = − iii) Si f es integrable en tres intervalos definidos a, b y c, entonces ( ) ( ) ( ) b c b a a c f x dx f x dx f x dx = + .
- 8. descubierta independientemente por Isaac Newton y Gottfried Leibniz y está enunciada en un teorema que recibe el nombre de teorema fundamental del cálculo. El teorema fundamental expresa que, para calcular una integral definida, se requiere calcular la antiderivada y luego evaluarla en los dos límites de integración. Ejemplo 1 Cálculo de una integral definida a) 9 9 3 2 4 4 4 2 3 xdx x = 3 3 2 2 4 4 (9) (4) 3 3 32 36 3 76 3 = − = − = b) 2 2 2 1 1 3 (3 1) 2 x dx x x − − + = + Teorema fundamental del cálculo Si una función ƒ es continua en el intervalo cerrado b a, y F es una antiderivada de ƒ en el intervalo b a, , entonces: ( ) ( ) ( ) b a f x dx F b F a = −
- 9. 2 2 3 3 (2) 2 ( 1) 1 2 2 3 (6 2) 1 2 1 8 2 15 2 = + − − − = + − − = − = c) dx x x dx x x ) ( 1 2 4 1 2 1 4 1 2 − − = − 12 47 1 3 2 4 1 3 16 1 3 2 4 1 4 3 2 3 2 3 4 1 1 2 3 = + − + = + − + = + = − x x d) ( ) 4 2 1 2 3 4 4 2 1 2 3 2 9 3 6 4 1 9 6 + + − = + + − x x x x dx x x x ( ) 64 679 2 1 8 9 4 1 64 1 4 72 128 64 = + + − − + + − = Al cambiar la variable x por la variable u al realizar una sustitución, los límites de la integral también deben cambiar.
- 10. Ejemplo Calculo de una integral definida usando u e) ( ) = − 26 2 3 3 1 3 2 6 1 1 3 u du dx x x 338 7 48 1 8112 1 12 1 2 6 1 6 1 26 2 2 2 26 2 3 = + − = − = − = = − − u u du u Uso de la integral definida para encontrar un área Ejemplo 1 Área bajo una curva a) Encontrar el área de la región limitada por la recta y = 2x + 1, el eje x, la recta x = 1 y x = 4. ( ) 4 4 2 1 1 2 1 A x dx x x = + = + ( ) ( ) ( ) ( ) 2 2 2 4 4 1 1 (16 4) (1 1) 20 2 18 A A A A u = + − + = + − + = − =
- 11. b) Encontrar el área de la región limitada por la curva y = 6 – x – x2 y el eje x. − − − = 2 3 2 ) 6 ( dx x x A 2 2 3 3 2 6 125 3 27 2 9 18 3 8 2 4 12 3 2 6 u A A x x x A = + − − − − − = − − = − c) Calcular el área de la región acotada por ( ) 1 f x x = + , el eje x y la recta x = 3. 2 3 2 3 1 2 2 1 0 0 3 3 2 1 3 2 2 2 1 3 2 ( 1) 3 2 (3 1) 0 3 16 3 A x dx u du u A x A A u − − = + = = = + = + − =
- 12. d) Encontrar el área de la región limitada por la curva y = x2 – x – 2 , el eje x y las rectas x = -2 y x = 2 1 2 2 2 2 1 1 2 3 2 3 2 2 1 ( 2) ( 2) 2 2 3 2 3 2 1 1 8 4 8 4 1 1 2 4 4 2 3 2 3 2 3 2 3 2 A x x dx x x dx x x x x A x x A − − − − − − = − − + − − − = − − − − − = − − + − − − + − − + − − − + 2 19 3 A u = Ejemplo 2 Cálculo de un área con la regla del seno fCalcular el área de la región acotada por y = senx, el eje x, x = 3 , x = 3 2 2 3 2 3 3 2 3 1 5 . 0 5 . 0 ) º 60 cos( ) º 120 cos( cos u A A A x A dx senx A = + = + − = − = =
- 13. PRÁCTICA N°6 I. Evalúe la integral definida. 1. dx x x ) 1 2 ( 3 2 2 + − = R: 3 7 2. dx x 3 2 1 2 1 = R: 3 5 3. dx x − + 1 1 5 ) 1 ( = R: 3 32 4. dx x x 3 3 1 0 2 ) 1 ( 2 − = R: 6 1 − 5. dx x − 5 4 3 ) 3 ( 2 = R: 4 3 6. dx x − 2 3 1 3 10 = R: 9 38 7. dx x x 3 3 1 0 2 1 7 + = R: 28 15 8. dx x x x e ) ( 2 1 3 2 1 − − − − + = R: 2 1 2 3 e e + − 9. dx x x ) ( 2 1 3 + − R: 4 21 10. ( )dx x x + 4 0 3 3 R: 16 3 8 + 11. dx x e 1 1 R: 1 12. dx x − 0 2 3 2 R: 3 4 5 6 1. 2 2 1 3 1 dy y − R: 2 1 14. dx x 2 0 1 ) 3 2 ( − + R: 3 13 15. dx x x x + − 3 1 2 2 3 5 4 2 R: 3 10
- 14. II. Use la integral definida para encontrar el área de la región limitada por la curva, el eje x y las rectas dadas. 1. y = 4x, x = 2 R: 8 2. y = 3x + 2, x = 2, x = 3 R: 2 19 3. y = x2, x = 2, x = 3 R: 3 19 4. y = 9 – x 2 R: 36 5. y = 3 + 2x –x2 R: 3 32 6. y = x 1 , x = 1, x = e R: 1 7. y = 1 2 − x , x = 1, x = 5 R: 3 26 8. y = x2 + 2, x = -1, x = 2 R: 9 9. y = x2- 2x, x = -3, x = -1 R: 3 50 10. y = 1 – x – x3, x = -2, x = 0 R: 8 11. y = –x2 – 2x, x = -3, x = 2 R: 3 28 12. y = 3x2 – 3, x = -2, x = 2 R: 12 13. y = x3 – 3x2 + 2x, x = 0, x = 2 R: 2 1
- 15. 14. y = x3 – 4x, x = -2, x = 2 R: 8 15. y = x1/3, x = -1, x = 8 R: 4 51 16. y = 4 – x2, x = 0, x = 2 R: 3 16 17. y = 2 + x – x2, x = -1, x = 2 R: 4.5 18. y = 1 1 + x , x = 0, x = 1 R: ln2
- 16. 2.2 Área de la región entre curvas Es posible extender la aplicación de la integral definida para el área de una región bajo una curva, al área de la región entre dos curvas. Consideremos dos funciones f y g, continuas en el intervalo [a, b]. Además, las gráficas de f y g se encuentran por encima del eje x, y la gráfica de g se encuentra por debajo de la gráfica de f. En este caso, puede interpretarse geométricamente, el área de la región entre las gráficas de f y g como el área de la región bajo la gráfica de g restada del área de la región el área de la región bajo la gráfica de f. Definición de área entre dos curvas Si f y g son continuas en , a b , y ( ) ( ) g x f x para toda x en , a b , entonces el área de la región acotada por las gráficas de f y g , y las rectas x a = y x b = es: dx x g x f A b a − = ) ( ) (
- 17. Ejemplo 1 Encontrar el área de una región entre dos curvas a) Encontrar el área de la región limitada por las curvas f(x) = 4x – x2 + 8 y g(x) = x2 - 2x. ( ) ( ) ( ) 2 4 1 2 3 4 1 2 4 1 2 2 3 125 3 2 41 8 3 3 2 32 48 3 128 8 2 6 3 2 8 6 2 2 8 4 u A A x x x A dx x x A dx x x x x A = = − + − + + − = + + − = + + − = − − + − = − − − b) Encontrar el área de la región limitada por las curvas f(x) = 9 – x2 y g(x) = x2 + 1, entre x = 0 y x = 3. Entre 0 y 3, se forman dos regiones A1 y A2. Luego el área buscada es: 1 2 A A A = + ( ) ( ) ( ) 2 2 2 1 0 2 2 1 0 2 3 1 0 2 1 9 1 2 8 2 8 3 16 32 16 3 3 A x x dx A x dx x A x A u = − − + = − + − = + − = + =
- 18. ( ) ( ) ( ) 2 2 3 2 3 2 3 2 2 2 3 2 2 2 2 3 14 16 3 16 24 3 54 8 3 2 8 2 9 1 u A x x A dx x A dx x x A = − − − = − = − = − − + = Luego el área total es 2 2 1 3 46 3 14 3 32 u A A A A = + = + = c) Hallar el área comprendida entre la parábola y2 = 4x y la recta y = 2x – 4. 2 4 2 2 3 4 2 2 4 2 2 9 6 15 4 1 12 8 8 4 12 64 2 4 12 2 2 4 4 2 4 u A A A y y y A dy y y A dy y y A = − = − + − + + − = + + − = + + − = − + = − − −
- 19. PRÁCTICA N°7 Encuentre el área de la región limitada por las gráficas de las ecuaciones dadas. 1. y = x2, y = 2x R: 3 4 2. y = x2, x = 0, y = 4 (x0) R: 3 16 3. y = x2 + 2, y = 8 R: 6 8 4. x = 8 + 2y, x = 0, y = -1, y = 3 R:40 5. y = 4 – x2, y = -3x R: 6 125 6. y2 = x, y = x – 2 R: 2 9 7. 2y = 4x – x2, 2y = x – 4 R: 12 125 8. y2 = x, 3x – 2y = 1 R: 81 32 9. y = 8 – x2, y = x2, x = -1, x = 1 R: 3 44 10. y = x2, y = 2, y = 5 R: ) 2 2 5 5 ( 3 4 − 11. y = x2, x + y = 2, eje x R: 6 5 12. y = x2 – 4, y = -x2 – 2x, x = -3, x = 1 R: 3 38 13. y = 4 – x2, y = -x + 2, x = -2, x = 3 R: 6 49
- 20. 14. y = - x2 + 3x, y = 2x3 – x2 – 5x, x = -2, x = 2 R: 16 15. y = x2 – 1, y = 7 – x2 R: 3 64 16. y = x2 + 1, y = 3x – 1, R: 6 1 17. y = ex, y = x- 1, x = -2, x = 0 R: 5 – e-2 18. y = x3, y = 3x + 2 R: 4 27