ejercicios programación lineal
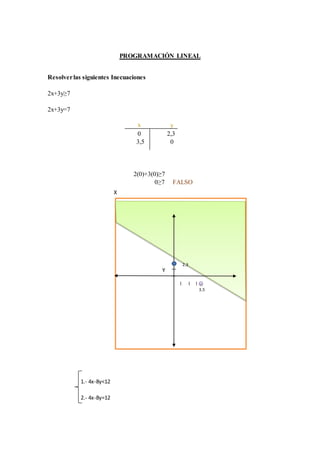
- 1. PROGRAMACIÓN LINEAL Resolverlas siguientes Inecuaciones 2x+3y≥7 2x+3y=7 x y 0 2,3 3,5 0 2(0)+3(0)≥7 0≥7 FALSO 1.- 4x-8y<12 2.- 4x-8y=12 X Y 3,5 2,3
- 2. x y 0 -1,5 3 0 4(0)+8(0)<12 0<12 VERDADERO 3.- 2𝑥 − 𝑦 > 0 2𝑥 = 𝑦 x y 0 0 1 2 X Y 3 -1,5 𝑃(2,0) 2(2) − 0 > 0 4 > 0 → Verdadero
- 3. 4.- { 4𝑥2 + 4𝑦2 ≥ 36 𝑥 + 5𝑦 < 7 { 4𝑥2 + 4𝑦2 = 36 𝑥 + 𝑦 = 7 𝑥2 + 𝑦2 = 9 𝑃(0,0) 4(0)2 + 4(0)2 ≥ 36 0 ≥ 36 → Falso 5.- 𝟒𝒙 𝟐 + 𝟑𝒚 𝟐 < 12 𝟐𝒙 + 𝟑 > y 𝑥 + 5𝑦 = 7 x Y 0 7 5⁄ 7 0 𝑃(0,0) 0 < 7
- 4. 𝟒𝒙 𝟐 + 𝟑𝒚 𝟐 = 12 𝑥2 3 𝑦2 4 = 1 X: √3 = 1,7 Y: √4 = 2 P(0,0) 4(02) + 3(02) <12 0 < 12 Verdadero 2x-y=-3 x y 0 3 -1,5 0 P(0,0) 2𝑥 − 𝑦 > -3 2(0)-(0) >-3 0>--3 Verdadero
- 5. 6. 3x2+y>6 2x2-y2<4 COMPROBACIÓN P(0,0) P(0,0) (1) (2) 3(0)2+(0)>6 2(0)2-(0)2<4 0>6 0<4 FALSO VERDAD GRÁFICO (1) (2) 3x2+y=6 y=6-3x2 2x2-y2=4 𝑥 = ±√ 4 + 𝑦2 2 x y x y -3 -21 ±2.6 -3 -2 -6 ±2 -2 -1 0 1 2 3 3 6 3 -6 -21 ±1.6 ±1.4 ±1.6 ±2 ±2.6 -1 0 1 2 3
- 6. 1.- Una Compañía de Auditores se especialista en preparar liquidaciones y auditorías de pequeñas empresas. Tiene interés en saber cuántas auditorías y liquidaciones pueden realizarse mensualmente para maximizar sus ingresos? Se dispone de 600 horas de trabajo directo y 220 horas para revisión, además aporta un ingreso de $250, una liquidación de impuestos requiere de 6 horas de trabajo directo y 4 de revisión producen un ingreso de $90, una auditoría requiere de 30 horas de trabajo directo y 8 de revisión, aporta con un ingreso de $250. El máximo de liquidaciones posibles es de 50. TABLA DE DATOS DESCRIPCIÓN TRABAJO DIRECTO REVISIÓN INGRESOS MÁXIMO LIQUIDACIONES 8 2 90 50 AUDITORÍAS 1 1 250 DISPONIBILIDAD 600 220 FUNCIÓN OBJETIVO. Max. Z=90x+250y RESTRICCIONES (1) 6x+30y≤ 600 (2) 4x+8y≤ 200 (3) x≤50 RESTRICCIONES DE NO NEGATIVIDAD (4) x,y0 SISTEMAS ECUACIONES (1) (2) (3) 6x+30y=600 4x+8y=200 x=50 x y x y 100 0 0 27,5 0 20 55 0
- 7. COMPROBACIÓN P(0,0) P(0,0) P(0,0) (1) (2) (3) 6(0)+30(0)≤600 4(0)+8(0)≤ 200 0≤50 0≤600 0≤ 200 VERDAD VERDAD VERDAD GRÁFICO ARCO CONVEXO C. SOLUCIÓN ÓPTIMA Punto x y z A 0 0 0 B 0 20 1050 C 25 15 6000 D 50 0 4500 (1) -24x-120y= -2400 (2) 24x+48y= 1200 y=15 x=25
- 8. Z= 1050 VALORES ÓPTIMOS x= 3 y=2 RESTRICCIONES ACTIVAS: 2,3 RESTRICCIONES INACTIVAS: 1
- 9. 2.- Un frutero necesita 16 cajas de naranjas, 5 de plátanos y 20 de manzana. Dos mayoristas pueden suministrarle para satisfacer sus necesidades pero solo venden la fruta en contenedores completos. El mayorista A envía en cada contenedor 8 cajas de naranjas, 1 de plátanos y 2 de manzanas. El mayorista B envía en cada contenedor 2 cajas de naranja, 1 de plátano y 7 de manzanas si se sabe que el mayorista A se encuentra a 150 km de distancias y el mayorista B a 30 km. Determine cuantos contenedores habrá que comparar a cada mayorista con el objeto de ahorrar tiempo dinero y minimizar la distancia. TABLA DE DATOS DESCRIPCIÓN A B DISPONIBILIDAD NARANJA 8 2 16 PLÁTANOS 1 1 5 MANZANAS 2 7 20 DISTANCIA 150 30 FUNCIÓN OBJETIVO. Min. Z=150x+30y RESTRICCIONES (1) 8x+2y16 (2) x+y5 (3) 2x+7y20 RESTRICCIONES DE NO NEGATIVIDAD (4) x,y0 SISTEMAS ECUACIONES (1) 8x+2y=16 (2) x+y=5 (3) 2x+7y=20 COMPROBACIÓN P(0,0) P(0,0) P(0,0) (1) 8(0)+2(0)16 (2) 0+05 (3) 2(0)+7(0)20 016 05 020 FALSO FALSO FALSO x y 0 8 2 0 x y 0 5 5 0 x y 0 2,9 10 0
- 10. GRÁFICO ARCO CONVEXO B. C. (2) -2A-2B= -10 (3) 2A+7B= 20 B=2 A=3 SOLUCIÓN ÓPTIMA Z= 1050 VALORES ÓPTIMOS x= 3 y=2 RESTRICCIONES ACTIVAS: 2,3 RESTRICCIONES INACTIVAS: 1 Punto x y z A 10 0 1500 B 3 2 1050 C 1 4 1350 D 0 8 2400 (1) -8A-8B= -40 (2) 8A+2B= 10 B=4 A=1
- 11. 3.- MAXIMIZAR FUNCIÓN OBJETIVO 𝑍 = 5 2 𝑥 + 𝑦 SUJETO A (1) 3𝑥 + 5𝑦 ≤ 15 (2) 5𝑥 + 2𝑦 ≤ 10 CONDICIONES TÉCNICAS 𝑥 ≥ 0 O 𝑗 = 1; 2 GRÁFICO (1) (2) 3x+5y=15 5x+2y=10 x y 0 3 5 0 0 ≤ 15 x y 0 5 2 0 0 ≤ 10
- 12. ARCO CONVEXO C. RESPUESTA Este problema tiene múltiples soluciones. SOLUCIÓN ÓPTIMA Z1= 5 Z2=5 VALORES ÓPTIMOS x1= 20/19 y1=45/19; x2=2 y2=0 RESTRICCIONES ACTIVAS: 1,2 NO HAY RESTRICCIONES INACTIVAS Punto X Y Z A 0 0 0 B 0 3 3 C 20 19 45 19 5 D 2 0 5 −15𝑥 − 25𝑦 = −75 15𝑥 + 6𝑦 = 30 𝑦 = 𝟒𝟓 𝟏𝟗 3𝑥 + 5 ( 45 19 ) = 15 𝑥 = 𝟐𝟎 𝟏𝟗
- 13. 4.- MAXIMIZAR FUNCIÓN OBJETIVO Z= 2x+3y SUJETO A (1) x≤2 (2) y≥4 (3) 2x+y≥5 CONDICIÓN TÉCNICA (4) x,y 0 SISTEMA DE ECUACIONES COMPROBACIÓN P(0,0) P(0,0) P(0,0) (1) (2) (3) x≤2 y≥4 2x+y≥5 0≤2 04 05 VERDAD FALSO FALSO (1) (2) (3) x=2 y=4 2x+y=5 x y 0 5 5/2 0
- 14. GRÁFICO ARCO CONVEXO PUNTOS x y z A 2 4 16 B 1/2 4 13 C 0 5 15 B. SOLUCIÓN ÓPTIMA Z= 16 VALORES ÓPTIMOS x= 2 y=4 RESTRICCIONES ACTIVAS: 1,2 RESTRICCIONES INACTIVAS: 3 (3) -2x-y= -5 (2) y= 4 x=1/2 y=4
- 15. 5.- MAXIMIZAR FUNCIÓN OBJETIVO Z= 2x+3y RESTRICCIONES (1) x≤2 (2) y≤3 (3) 2x+y≥18 RESTICCIONES DE NO NEGATIVIDAD (4) x+y≥0 SISTEMAS DE ECUACIONES COMPROBACIÓN P(0,0) P(0,0) P(0,0) (1) (2) (3) x≤2 y≤3 2x+y≥18 0≤2 0≤3 018 VERDAD VERDAD FALSO GRÁFICO RESPUESTA: El problema no tiene solución x y 0 18 9 0 (1) (2) (3) x=2 y=3 2x+y=18
- 16. 6.- Una compañía produce automóviles y camiones, cada vehículo tiene que pasar por un taller de pintura y un taller de montaje de carrocería si el taller de pintura pinta solamente camiones, se podría pintar 40 camiones al día y si pinta solo automóviles se podrían pintar 60 automóviles si el taller de carrocerías ensamblara solo camiones podría ensamblar 50 camiones al día y si ensamblaría solo automóviles podrían ensamblar 50 automóviles al día cada camión aporta $300 a la utilidad y cada automóvil $200. Maximice la utilidad. Pintura PENDIENTE P1(0,40) 𝑚 = 𝑦2−𝑦1 𝑥2−𝑥1 P2(60,0) 𝑚 = 40−0 0−60 𝒎 = − 𝟐 𝟑 Ensamblaje PENDIENTE ECUACIÓN DE LA RECTA P(0,50) 𝑚 = 𝑦2−𝑦1 𝑥2−𝑥1 y-y1=m(x-x1) P(50,0) 𝑚 = 50−0 0−50 y-50=-1 (x) 𝒎 = −𝟏 x+y=50 FUNCIÓN OBEJTIVO Z= 200x+ 300y RESTRICCIONES (1) 2x+3y ≤ 120 (2) x+y ≤ 50 RESTRICCIONES DE NO NEGATIVIDAD (3) x,y0 ECUACIÓN DE LA RECTA y-y1=m(x-x1) y-40=-2/3 (x) 3y-120=-2x 2x+3y=120
- 17. SISTEMAS DE ECUACIONES COMPROBACIÓN P(0,0) P(0,0) (1) (2) 2(0)+3(0)≤120 (0)+(0)≤ 50 0≤120 0≤ 50 VERDAD VERDAD GRÁFICO (1) (2) 2x+3y=120 x+y=50 x y x y 60 0 0 50 0 40 50 0
- 18. ARCO CONVEXO C. RESPUESTA El problema tiene múltiples soluciones. SOLUCIÓN ÓPTIMA Z1= 12000 Z2=12000 VALORES ÓPTIMOS x1= 0 y1=40; x2=30 y2=20 RESTRICCIONES ACTIVAS: 1,2 NO HAY RESTRICCIONES INACTIVAS Punto x y z A 0 0 0 B 0 40 12000 C 30 20 12000 D 50 0 10000 (1) -2x-3y= -120 (2) 2x+2y= 100 y=20 x=30
- 19. 7.- En una pastelería se hace 2 tipos de torta. Vienesa y Real. Cada torta Vienesa necesita ¼ de relleno por cada Kg de bizcocho y produce un beneficio de $250. Una torta Real necesita ½ kg de relleno por cada kg de Bizcocho y produce $400 de beneficio en la pastelería e pueden hacer diariamente hasta 150kg de bizcocho y 50kg de relleno. Por problemas de la maquina o se pueden hacer más de 125 tortas de cada tipo. Determine cuantas tortas de cada tipo deben venderse al día para maximizar el beneficio. FUNCIÓN OBJETIVO MAX. Z= 250x + 400y RESTRICCIONES (1) x +y ≤ 150 (2) 0,250x + 0,500y ≤ 50 (3) X ≤ 125 (4) y ≤ 125 RESTRICCIONES DE NO NEGATIVIDAD (5) x, y ≥ 0 SISTEMAS ECUACIONES COMPROBACIÓN P(0,0) P(0,0) P(0,0) (1) (2) (3) (0)+(0)≤150 0,250(0)+0,500(0)≤ 50 0≤125 VERDAD 0≤150 0≤ 50 (4) VERDAD VERDAD 0≤125 VERDAD (1) (2) (3) (4) x+y=150 0,250x+0,500y=50 x=125 y=125 X y x Y 150 0 0 100 0 150 200 0
- 20. GRÁFICO ARCO CONVEXO C. SOLUCIÓN ÓPTIMA Z= 131200 VALORES ÓPTIMOS x= 125 y=25 RESTRICCIONES ACTIVAS: 2,3 RESTRICCIONES INACTIVAS: 1 Punto x Y Z A 0 0 0 B 0 100 40000 C 50 100 32500 D 125 25 131200 E 125 0 31250 (1) -0,250 x -0,250y ≤ -37,5 (2) 0,250x + 0,500y ≤ 50 y=50 x=100
- 21. 8.- Una joyería elaboro 2 modelos de joyas el primer modelo es 5, 5,20 y el segundo modelo es 5, 10,5, los números que se indican representan en porcentaje oro, plata, cobre la joyería dispone de 10kg de oro, 180 de plata y 200 kg de cobre por cada tipo de modelo 5, 5, 10 se obtiene una utilidad de $18,50 y por el otro modelo una utilidad de $20,00 maximice la utilidad establezca restricciones activas e inactivas y verifica si hay holgura o excedente. FUNCIÓN OBJETIVO Max Z= 8,50x + 20Y SUJETO A (1) 0,05X + 0,05y ≤ 110 (2) 0,05x + 0,10y ≤ 180 (3) 0,10x + 0,05y ≤ 200 RESTRICCIONES DE NO NEGATIVIDAD (4) x, y ≥ 0 SISTEMAS DE ECUACIONES COMPROBACIÓN P(0,0) P(0,0) P(0,0) (1) (2) (3) 0,05(0)+0,05(0)≤110 0,05(0)+0,10(0)≤ 180 0,10(0)+0,05(0)≤200 0≤110 0≤ 180 0≤200 VERDAD VERDAD VERDAD (1) (2) (3) 0,05X + 0,05y = 110 0,05x + 0,10y =180 0,10x + 0,05y = 200 x y x y x y 2200 0 0 1800 0 4000 0 2200 3600 0 2000 0
- 22. GRÁFICO C D (1) 0,05x + 0,05y = 110 (-1) (1) 0,05x + 0,05y = 110 (-1) (2) 0,05x + 0,10y= 180 (2) 0,10x + 0,05y= 200 - 0,05x - 0,05y = -110 0,05x - 0,05y = -110 0,05x+ 0,10y = 180 0,10x+ 0,05y = 200 0,05 y= 70 0,05 X = 90 Y= 1400 y= 1800 0,05x + 0,10 y = 180 0,10x + 0,05 y = 200 x= 800 x= 400 Z= 18,50(800) + 20(1400) Z= 18,50(1800) + 20(400) Z= 42800 Z= 41300 Arco Convexo Solución Óptima X Y Z Z= 42800 C 800 1400 42800 Valores Óptimos D 1800 400 41300 x= 800 Y= 1400 Cálculode la Holgura para el oro 0,05x + 0,05y ≤ 110
- 23. 0,05(800) + 0,05(1400) + h1 ≤ 110 h1 ≤ 0 Disponibilid. Ocupados Holgura Oro 110 110 0 Plata 180 180 0 Cálculode la Holgura para la plata Cobre 200 50 50 0,05x + 0,10y ≤ 180 0,05(800) + 0,10(1400) + h2 ≤ 180 Solución Óptima h2 ≤ 0 Z= 42800 Valores Óptimos x= 800 Cálculode la Holgura para el cobre Y= 1400 0,10x + 0,05y ≤ 200 h1= 0 0,10(800) + 0,05(1400) + h3 ≤ 200 h2= 0 h3 ≤ 50 h3= 50 Restricción Activa= 1,2 Restricción Inactiva= 3
- 24. 9. .- Un frutero necesita 16 cajas de naranjas, 5 de plátanos y 20 de manzana. Dos mayoristas pueden suministrarle para satisfacer sus necesidades pero solo venden la fruta en contenedores completos. El mayorista A envía en cada contenedor 8 cajas de naranjas, 1 de plátanos y 2 de manzanas. El mayorista B envía en cada contenedor 2 cajas de naranja, 1 de plátano y 7 de manzanas si se sabe que el mayorista A se encuentra a 150 km de distancias y el mayorista B a 30 km. Determine cuantos contenedores habrá que comparar a cada mayorista con el objeto de ahorrar tiempo dinero y minimizar la distancia. TABLA DE DATOS DESCRIPCIÓN A B DISPONIBILIDAD NARANJA 8 2 16 PLÁTANOS 1 1 5 MANZANAS 2 7 20 DISTANCIA 150 30 FUNCIÓN OBJETIVO. Min. Z=150x+30y RESTRICCIONES (1) 8x+2y16 (2) x+y5 (3) 2x+7y20 RESTRICCIONES DE NO NEGATIVIDAD (4) x,y0 SISTEMAS ECUACIONES (2) 8x+2y=16 (2) x+y=5 (3) 2x+7y=20 COMPROBACIÓN P(0,0) P(0,0) P(0,0) (2) 8(0)+2(0)16 (2) 0+05 (3) 2(0)+7(0)20 016 05 020 FALSO FALSO FALSO x y 0 8 2 0 x y 0 5 5 0 x y 0 2,9 10 0
- 25. GRÁFICO ARCO CONVEXO B. C. (2) -2A-2B= -10 (3) 2A+7B= 20 B=2 A=3 SOLUCIÓN ÓPTIMA Z= 1050 VALORES ÓPTIMOS x= 3 y=2 RESTRICCIONES ACTIVAS: 2,3 RESTRICCIONES INACTIVAS: 1 Cálculode Excedente de Naranja 8x + 2y ≥ 16 8(5) + 2(2) - 16≥ E1 12≥ E1 Punto x y z A 10 0 1500 B 3 2 1050 C 1 4 1350 D 0 8 2400 (1) -8A-8B= -40 (2) 8A+2B= 10 B=4 A=1
- 26. Cálculode Excedente de Plátano x + y ≥ 5 (5) + (2) ≥ 5 + E2 E2 ≤ 0 Cálculode Excedente de Manzanas 2x + 7y ≥ 20 2(5) + 7(2) ≥ 20 + E3 E3 ≥ 0 PROBLEMA DUAL P.PRIMAL Max Z= 5X1 + 6X2 S.A. (1) X1+9X2 ≤ 60 (2) 2X1+3X2≤ 45 (3) 5X1-2X2≤20 (4) X2 ≤ 30 X1,X2 0 VERDAD VERDAD VERDAD (1) (2) (3) X1+9X2=60 2X1+3X2=45 5X1- 2X2=20 X1 X2 X1 X2 A B 0 6,7 0 15 0 -10 60 0 22,5 0 4 0
- 27. GRÁFICO Z = 67,56 6,36+9(5,96)+ h1 60 2 (6,36)+3(5,96)+ h2 45 5 (6,36)- 2(5,96)+ h3 20 h1 = 0 h2 = 14 h3 = 0 5,96+ h4 30 h4 ≤ 24 P.DUAL MIN Z= 60Y1 + 45Y2 + 20Y3 + 30Y4 S.A. (1) Y1+2Y2+5Y3 ≥ 5 (2) 9Y1+3Y2-2Y3≥ 6 (3) Y1,Y2,Y3,Y4 ≥0 (1) 5X1 – 2X2 = 20 (2) -5X1- 45X2= -300 X2= 5,96 X1= 6,36 (1) -9Y1 - 45Y3 = -45 (2) 9Y1 - 2Y3 = 6
- 28. Z = 60( 𝟒𝟎 𝟒𝟕 ) + 20( 𝟑𝟗 𝟒𝟕 ) Z= 67,65 Y3 = 𝟑𝟗 𝟒𝟕 Y1 = 𝟒𝟎 𝟒𝟕