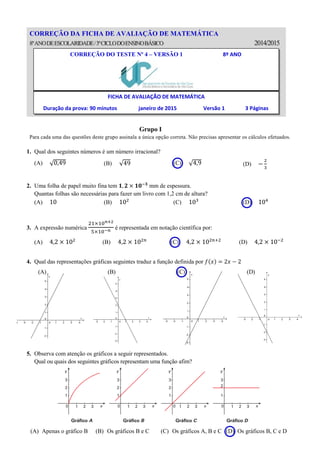
1. CORREÇÃO DA FICHA DE AVALIAÇÃO DE MATEMÁTICA
8ºANODEESCOLARIDADE/3ºCICLODOENSINOBÁSICO 2014/2015
Grupo I
Para cada uma das questões deste grupo assinala a única opção correta. Não precisas apresentar os cálculos efetuados.
1. Qual dos seguintes números é um número irracional?
(A) √0,49 (B) √49 (C) √4,9 (D) −
2
3
2. Uma folha de papel muito fina tem 𝟏, 𝟐 × 𝟏𝟎−𝟑
mm de espessura.
Quantas folhas são necessárias para fazer um livro com 1,2 cm de altura?
(A) 10 (B) 102
(C) 103
(D) 104
3. A expressão numérica
21×10 𝑛+2
5×10−𝑛
é representada em notação científica por:
(A) 4,2 × 102
(B) 4,2 × 102𝑛
(C) 4,2 × 102𝑛+2
(D) 4,2 × 10−2
4. Qual das representações gráficas seguintes traduz a função definida por 𝑓(𝑥) = 2𝑥 − 2
(A) (B) (C) (D)
5. Observa com atenção os gráficos a seguir representados.
Qual ou quais dos seguintes gráficos representam uma função afim?
(A) Apenas o gráfico B (B) Os gráficos B e C (C) Os gráficos A, B e C (D) Os gráficos B, C e D
CORREÇÃO DO TESTE Nº 4 – VERSÃO 1 8º ANO
FICHA DE AVALIAÇÃO DE MATEMÁTICA
Duração da prova: 90 minutos janeiro de 2015 Versão 1 3 Páginas

2. Grupo II
Apresenta o teu raciocínio de forma clara, indicando todos os cálculos que tiveres de efetuar e todas as justificações necessárias.
6. Observa a figura onde 𝐷𝐶//𝐸𝐵
6.1. Justifica que os triângulos [𝐴𝐵𝐸] e [𝐴𝐶𝐷] são
semelhantes.
Os triângulos [𝑨𝑩𝑬] e [𝑨𝑪𝑫] são semelhantes pelo critério AA,
pois têm dois ângulos geometricamente iguais:
 𝑨𝑩̂ 𝑬 = 𝑨𝑪̂ 𝑫 = 𝟗𝟎°
 𝑬𝑨̂ 𝑩 = 𝑫𝑨̂ 𝑪 (ângulo de vértice comum)
6.2. Determina 𝐴𝐶̅̅̅̅.
Como os triângulos [𝑨𝑩𝑬] e [𝑨𝑪𝑫] são semelhantes, os lados correspondentes são diretamente
proporcionais, isto é:
𝑨𝑩̅̅̅̅
𝑨𝑪̅̅̅̅
=
𝑬𝑩̅̅̅̅
𝑫𝑪̅̅̅̅
⇔
𝟏𝟐
𝑨𝑪̅̅̅̅
=
𝟖
𝟏𝟎
⟺ 𝑨𝑪̅̅̅̅ =
𝟏𝟐 × 𝟏𝟎
𝟖
⟺ 𝑨𝑪̅̅̅̅ =
𝟏𝟐𝟎
𝟖
⟺ 𝑨𝑪̅̅̅̅ = 𝟏𝟓
Logo 𝑨𝑪̅̅̅̅ = 𝟏𝟓 metros
6.3. Determina 𝐴𝐷̅̅̅̅. Apresenta o resultado em metros, com aproximação às centésimas.
Aplicando o Teorema de Pitágoras ao triângulo [𝑨𝑪𝑫],
𝑨𝑫̅̅̅̅ 𝟐
= 𝑨𝑪̅̅̅̅ 𝟐
+ 𝑪𝑫̅̅̅̅ 𝟐
⇔ 𝑨𝑫̅̅̅̅ 𝟐
= 𝟏𝟓 𝟐
+ 𝟏𝟎 𝟐
⇔ 𝑨𝑫̅̅̅̅ 𝟐
= 𝟐𝟐𝟓 + 𝟏𝟎𝟎 ⇔ 𝑨𝑫̅̅̅̅ 𝟐
= 𝟑𝟐𝟓 ⇔ 𝑨𝑫̅̅̅̅ = ±√𝟑𝟐𝟓 ⇒
⇒ 𝑨𝑫̅̅̅̅ = √𝟑𝟐𝟓 ⇔ 𝑨𝑫̅̅̅̅ ≈ 𝟏𝟖, 𝟎𝟑 𝒎𝒆𝒕𝒓𝒐𝒔 (𝟐 𝒄𝒂𝒔𝒂𝒔 𝒅𝒆𝒄𝒊𝒎𝒂𝒊𝒔)
Logo 𝑨𝑫̅̅̅̅ ≈ 𝟏𝟖, 𝟎𝟑 𝒎𝒆𝒕𝒓𝒐𝒔
7. Completa a figura ao lado sabendo que a reta r é um eixo de reflexão da
figura:
8. Na figura ao lado está representado um quadriculado.
Usando as letras da figura, determina:
8.1. 𝐴𝐵⃗⃗⃗⃗⃗ + 𝐴𝑀⃗⃗⃗⃗⃗⃗ = 𝐀𝐁⃗⃗⃗⃗⃗ + 𝐁𝐍⃗⃗⃗⃗⃗⃗ = 𝐀𝐍⃗⃗⃗⃗⃗⃗
8.2. 𝑁𝐼⃗⃗⃗⃗ + 𝐼𝑉⃗⃗⃗⃗ = 𝐍𝐕⃗⃗⃗⃗⃗
8.3. 𝑁𝑂⃗⃗⃗⃗⃗⃗ + 𝐽𝐻⃗⃗⃗⃗ = 𝐍𝐎⃗⃗⃗⃗⃗⃗ + 𝐎𝐌⃗⃗⃗⃗⃗⃗⃗ = 𝐍𝐌⃗⃗⃗⃗⃗⃗⃗
8.4. 𝑃𝐿⃗⃗⃗⃗ + 𝑃𝐻⃗⃗⃗⃗⃗⃗ = 𝐏𝐋⃗⃗⃗⃗⃗ + 𝐋𝐃⃗⃗⃗⃗⃗ = 𝐏𝐃⃗⃗⃗⃗⃗
8.5. Considera a translação em que o transformado do
ponto 𝐻 é o ponto 𝐷. Qual é, por meio dessa
translação, o transformado do triângulo [𝑁𝐼𝑉]?
𝑻 𝑯𝑫⃗⃗⃗⃗⃗⃗ ([𝑵𝑰𝑽]) = [𝑱𝑬𝑹]
9. Identifica as simetrias que podes observar no friso da figura seguinte:
As simetrias que se podem observar no friso são simetrias de reflexão, simetrias de translação e
simetrias de reflexão deslizante.

3. 10.Associa cada uma das representações gráficas das funções afins 𝒇, 𝒈, 𝒉 e 𝒊 à respetiva expressão algébrica.
O gráfico 𝑨 corresponde à função linear 𝒈(𝒙); o gráfico 𝑩 corresponde à função linear 𝒊(𝒙); o
gráfico 𝑪 corresponde à função afim 𝒇(𝒙) e o gráfico 𝑫 corresponde à função afim 𝒉(𝒙).
11.Escreve a expressão algébrica de uma função afim 𝒇, sabendo que:
11.1. O seu gráfico é uma reta paralela ao da função 𝒋(𝒙) = −𝟑𝒙 + 𝟓 e passa no ponto (0, −2).
A função afim 𝒇(𝒙) tem declive −𝟑 e ordenada na origem −𝟐, pelo que a expressão algébrica da
função é 𝒇(𝒙) = −𝟑𝒙 − 𝟐 ou 𝒚 = −𝟑𝒙 − 𝟐.
11.2. O seu gráfico é uma reta que passa nos pontos (1, 3) e (2,5)
Se o gráfico da função afim 𝒇(𝒙) passa nos pontos (𝟏, 𝟑) e (𝟐, 𝟓), então o declive é dado pela
expressão 𝒂 =
𝒚 𝟏−𝒚 𝟐
𝒙 𝟏−𝒙 𝟐
⟺ 𝒂 =
𝟓−𝟑
𝟐−𝟏
⟺ 𝒂 =
𝟐
𝟏
⟺ 𝒂 = 𝟐. Para calcular a ordenada na origem basta
substituir as coordenadas de um dos pontos dados da reta na expressão algébrica 𝒚 = 𝟐𝒙 + 𝒃, isto
é, 𝟑 = 𝟐 × 𝟏 + 𝒃 ⟺ 𝟑 = 𝟐 + 𝒃 ⟺ 𝟑 − 𝟐 = 𝒃 ⟺ 𝒃 = 𝟏.
Logo, a expressão algébrica da função afim pedida é 𝒇(𝒙) = 𝟐𝒙 + 𝟏 ou 𝒚 = 𝟐𝒙 + 𝟏.
12.Considera as funções 𝒇, 𝒈 e 𝒉 tais que:
 𝒇(𝒙) é uma função linear, cujo gráfico é uma reta paralela ao gráfico da função 𝒈
 𝒈(𝒙) = 𝟑𝒙 − 𝟐;
 𝒉(𝒙) = −𝟐𝒙 + 𝟏
12.1. Escreve a expressão algébrica da função 𝑓.
𝒇(𝒙) = 𝟑𝒙 ou 𝒚 = 𝟑𝒙
12.2. Representa graficamente a função 𝑔(𝑥).
𝒙 𝒈(𝒙) = 𝟑𝒙 − 𝟐
0 𝒈(𝟎) = 𝟑 × 𝟎 − 𝟐 = 𝟎 − 𝟐 = −𝟐
1 𝒈(𝟏) = 𝟑 × 𝟏 − 𝟐 = 𝟑 − 𝟐 = 𝟏
2 𝒈(𝟐) = 𝟑 × 𝟐 − 𝟐 = 𝟔 − 𝟐 = 𝟒
12.3. Mostra que o ponto (1, −1) pertence ao
gráfico da função 𝒉, mas não pertence ao
gráfico da função 𝒈.
Basta verificar que 𝒉(𝟏) = −𝟏 e 𝒈(𝟏) ≠ −𝟏.
De facto, 𝒉(𝟏) = −𝟐 × 𝟏 + 𝟏 = −𝟐 + 𝟏 = −𝟏 e
𝒈(𝟏) = 𝟑 × 𝟏 − 𝟐 = 𝟑 − 𝟏 = 𝟏 ≠ −𝟏.
Logo, o ponto (𝟏, −𝟏) pertence ao gráfico da função 𝒉, mas não pertence ao gráfico da
função 𝒈.