Geometry toolbox advanced proofs (3)
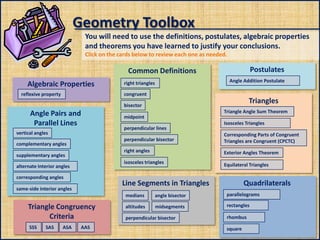
- 1. Geometry Toolbox You will need to use the definitions, postulates, algebraic properties and theorems you have learned to justify your conclusions. Click on the cards below to review each one as needed. Postulates Common Definitions Algebraic Properties Angle Addition Postulate right triangles congruent reflexive property Triangles bisector Angle Pairs and Parallel Lines vertical angles Triangle Angle Sum Theorem midpoint perpendicular lines Isosceles Triangles perpendicular bisector right angles supplementary angles alternate Interior angles corresponding angles Exterior Angles Theorem isosceles triangles complementary angles Corresponding Parts of Congruent Triangles are Congruent (CPCTC) Equilateral Triangles Line Segments in Triangles same-side interior angles Quadrilaterals medians Triangle Congruency Criteria SSS SAS ASA AAS angle bisector parallelograms altitudes midsegments rectangles perpendicular bisector rhombus square
- 2. Parallelogram Properties of parallelograms: Opposite sides are parallel Opposite sides are congruent Opposite angles are congruent Consecutive angles are supplementary Diagonals are bisect each other Opposite sides are parallel Opposite angles are congruent Opposite sides are congruent Consecutive angles are supplementary Diagonals bisect each other
- 3. Rhombus Properties of Rhombuses: All properties of parallelograms apply to rhombus: Opposite sides are parallel Opposite sides are congruent Opposite angles are congruent Consecutive angles are supplementary Diagonals bisect each other and All sides are congruent Diagonals bisect opposite angles Diagonals are perpendicular All sides are congruent Diagonals are perpendicular Diagonals bisect opposite angles
- 4. Rectangle Properties of Rectangles: Diagonals are congruent
- 5. Square Properties of Squares: All sides are congruent Diagonals are perpendicular Diagonals are congruent Diagonals bisect opposite angles
- 7. Supplementary Angles Supplementary angles are two angles whose measures add up to 180°. Each angle is called the supplement of the other. The angles may or may not be adjacent to each other. If m∠IJK=113° and the m∠KJL=67°, the sum is 180°. This means that ∠IJK and ∠KJL are supplementary angles. ∠IJL is a straight angle.
- 8. Vertical Angles Two lines that intersect form four angles. The angles that are opposite from each other are vertical angles. Vertical Angles Theorem: Vertical angles are congruent.
- 9. Angle Addition Postulate Angle Addition Postulate The sum of two adjacent angles is equal to the measure of the larger angle that is created. ∠ABC+∠CBD=∠ABD
- 10. Alternate Interior Angles Alternate interior angles are in between two parallel lines but on opposite sides of the transversal (creates "Z" or backwards "Z") Alternate Interior Angles Theorem If two parallel lines are cut by a transversal, then the alternate interior angles are congruent. Lines m and n are parallel and are intersected by line t. There are two pairs of alternate interior angles: ∠4≅∠6 ∠3≅∠5
- 11. Corresponding Angles Corresponding angles are the angles on the same side of the parallel lines and same side of the transversal. Corresponding Angles Postulate If two parallel lines are cut by a transversal, then the corresponding angles are congruent. Lines m and n are parallel and are intersected by line t. There are four pairs of corresponding angles: ∠1≅∠5 ∠2≅∠6 ∠4≅∠8 ∠3≅∠7
- 12. Same-Side Interior Angles Same-Side Interior Angles are the angles between the parallel lines and on the same side of the transversal. Same-Side Interior Angles If two parallel lines are cut by a transversal, then same-side interior angles are supplementary. Lines m and n are parallel and are intersected by line t. There are two pairs of same-side interior angles: ∠4+∠5=180° ∠3+∠6=180°
- 13. Exterior Angles An exterior angle is an angle that is outside of a polygon. The Triangle Exterior Angle Theorem The measure of the exterior angle is equal to the sum of the two remote interior angles. The remote interior angles are two interior angles of the triangle that are not adjacent to the exterior angle. m∠A + m∠B = m∠BCD
- 14. Right Triangles A right triangle is a triangle with one angle that is 90°. The side opposite the right angle is called the hypotenuse and the two sides that are not the hypotenuse are called legs. Acute Angles of a Right Triangle Theorem In a right triangle, the two acute angles are complementary.
- 15. Triangle Angle Sum Theorem
- 16. Bisectors The bisector of an angle divides an angle into two congruent angles. The bisector of a segment divides the segment into two congruent segments (and goes through the midpoint of the segment). Line Segment Bisector: LK is a line segment that bisects HJ, point M is the midpoint of HJ Angle Bisector: EG is a line segment that bisects ∠DGF
- 17. Midpoint The midpoint of a segment divides a segment into two congruent segments. If LK is a line segment that bisects HJ, point M is the midpoint of HJ and LK is a line bisector of HJ.
- 18. Reflexive Property (shared side or angle) If two triangles share a side, the two sides are congruent. If two triangles share an angle, the two angles are congruent.
- 19. Perpendicular Lines Perpendicular lines intersect to form 90° angles. (right angles)
- 20. Corresponding Parts (CPCTC) There are six statements that can be written about these triangles based on their corresponding, congruent parts. Corresponding Parts of Congruent Triangles are Congruent (CPCTC) Corresponding parts can be proved congruent using CPCTC if two triangles have already been proved congruent by one of the triangle congruence criteria (SSS, SAS, ASA, or AAS).
- 21. SSS Postulate If three sides of one triangle are congruent to three sides of another triangle, then the triangles are congruent. S S S
- 22. SAS Postulate If two sides and the included angle of one triangle are congruent to two sides and the included angle of another triangle, then the triangles are congruent. S S A
- 23. ASA Postulate If two angles and the included side of one triangle are congruent to two angles and the included side of another triangle, then the triangles are congruent. A A S
- 24. AAS Postulate If two angles and the non-included side of one triangle are congruent to two angles and the non-included side of another triangle, then the triangles are congruent. A A S
- 25. Congruent Angles, segments or figures that are congruent have exactly the same size and shape. This means that the measures of the angles or lengths of segments are equal.
- 26. Isosceles Triangles An isosceles triangle is a triangle with two congruent sides. The base of an isosceles triangle is the side that is not a leg. The base angles of an isosceles triangle are the angles that are opposite the two legs that are congruent. The vertex angle is the angle that is not a base angle (the angle that is opposite the base of the isosceles triangle). The altitude of the isosceles triangle is the line segment that is drawn from the vertex to the base of the isosceles triangle. The altitude of a triangle is always perpendicular to the base
- 27. Isosceles Triangles Altitude of an Isosceles Triangle Theorem If a line segment is the angle bisector of the vertex angle of an isosceles triangle, then it is also the perpendicular bisector of the base. Base Angles of Isosceles Triangles Theorem If a triangle is isosceles, the angles that are opposite the two congruent sides are also congruent.
- 28. Equilateral Triangles Equilateral triangles have all sides with the same length. An equiangular triangle is a triangle whose angles all have the same measure.
- 29. Perpendicular Bisector A perpendicular bisector is a line segment that divides a segment into two congruent parts and is perpendicular (creates a right angle) with the segment it intersects.
- 30. Right Angle A right angle has a measure of 90°. ∠RST is a right angle. The measure of ∠RST is 90°. Segment RS is perpendicular to segment ST. (RS⊥ST)
- 31. Midsegments The midsegment of a triangle is a segment that joins the midpoints of two sides of a triangle. The midpoint of a segment is the point that divides the segment in half. The Midsegment Theorem The midsegment is parallel to its third side. The midsegment is half of the length of the third side. The midsegment can be drawn from any two sides of a triangle through the midpoints. The midsegments do not intersect at one point.
- 32. Median The median of a triangle is a segment whose endpoints are a vertex in a triangle and the midpoint of the opposite side. When all three of the medians of a triangle are constructed, the medians of a triangle meet at a point called the centroid. Another word for centroid is the center of gravity, the point at which a triangular shape will balance. In this example, the medians intersect at point G. Point G is the centroid of the triangle.
- 33. Altitude If all three altitudes are drawn in a triangle, they meet at a point called the orthocenter. In this example, the three altitudes of this triangle meet at point R, the orthocenter.
- 34. Angle Bisector The angle bisector is a line segment that divides an angle in half. The angle bisectors of a triangle intersect at a point called the incenter. The incenter is the center of a circle that can be drawn inside of the triangle (inscribed in the triangle). The angle bisectors of this triangle intersect at point D, which is the incenter. A circle with center at point D can be inscribed inside ΔUVT.
- 35. Perpendicular Bisectors A perpendicular bisector is a line segment that is perpendicular to a line segment and goes through the midpoint of a line segment. The perpendicular bisectors of the sides of a triangle are concurrent at a point called the circumcenter. This point is the center of a circle that can be circumscribed around the triangle. The red lines represent the perpendicular bisectors of the sides of ΔFEG. The perpendicular bisectors intersect at point L, the circumcenter. Point L is the center of the circle that is circumscribed around ΔFEG.