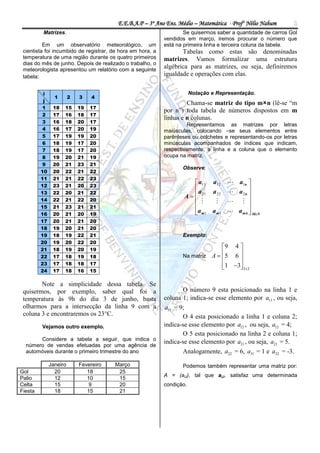
1. E.E.B.A.P – 3º Ano Ens. Médio – Matemática - Profº Nélio Nahum 1
Matrizes. Se quisermos saber a quantidade de carros Gol
vendidos em março, iremos procurar o número que
Em um observatório meteorológico, um está na primeira linha e terceira coluna da tabela.
cientista foi incumbido de registrar, de hora em hora, a Tabelas como estas são denominadas
temperatura de uma região durante os quatro primeiros matrizes. Vamos formalizar uma estrutura
dias do mês de junho. Depois de realizado o trabalho, o
meteorologista apresentou um relatório com a seguinte
algébrica para as matrizes, ou seja, definiremos
tabela: igualdade e operações com elas.
i Notação e Representação.
1 2 3 4
j
Chama-se matriz do tipo mn (lê-se “m
1 18 15 19 17
por n”) toda tabela de números dispostos em m
2 17 16 18 17
linhas e n colunas.
3 16 18 20 17
Representamos as matrizes por letras
4 16 17 20 19 maiúsculas, colocando –se seus elementos entre
5 17 19 19 20 parênteses ou colchetes e representando-os por letras
6 18 19 17 20 minúsculas acompanhados de índices que indicam,
7 18 19 17 20 respectivamente, a linha e a coluna que o elemento
Vejamos um exemplo: ocupa na matriz.
8 19 20 21 19
9 20 21 23 21
Considere a tabela a seguir, que indica o número de vendas efetuadas por uma agência de automóveis durante o pri
Observe:
10 20 22 21 22
11 21 21 22 23
12 23 21 20 23
 a11 a12  a1n 
a  a 2n 
13 22 20 21 22 a 22
A   21 
14 22 21 22 20      
15 21 23 21 21  
16 20 21 20 19 a m1 a m1  a mn  MxN
17 20 21 21 20
18 19 20 21 20
19 18 19 22 21 Exemplo:
20 19 20 22 20
21 18 19 20 19
9 4 

Na matriz A  5 6

22 17 18 19 18
 
23 17 18 18 17 1 3 3 x 2
 
24 17 18 16 15
Note a simplicidade dessa tabela. Se
quisermos, por exemplo, saber qual foi a O número 9 esta posicionado na linha 1 e
temperatura às 9h do dia 3 de junho, basta coluna 1; indica-se esse elemento por a11 , ou seja,
olharmos para a intersecção da linha 9 com a a11 = 9;
coluna 3 e encontraremos os 23°C. O 4 esta posicionado a linha 1 e coluna 2;
Vejamos outro exemplo. indica-se esse elemento por a12 , ou seja, a12 = 4;
O 5 esta posicionado na linha 2 e coluna 1;
Considere a tabela a seguir, que indica o
indica-se esse elemento por a21 , ou seja, a21 = 5.
número de vendas efetuadas por uma agência de
automóveis durante o primeiro trimestre do ano Analogamente, a22 = 6, a31 = 1 e a32 = -3.
Janeiro Fevereiro Março Podemos também representar uma matriz por:
Gol 20 18 25
A = (aiJ), tal que aiJ, satisfaz uma determinada
Palio 12 10 15
Celta 15 9 20 condição.
Fiesta 18 15 21

2. E.E.B.A.P – 3º Ano Ens. Médio – Matemática - Profº Nélio Nahum 2
Exemplo: Neste caso definimos duas diagonais, a
principal e a secundária, onde:
Escreva a matriz representada por:
a) A = (aij)2x2, tal que aij = i + j. a ij  DP  i  j
b) A = (aij)1x3, tal que aij = 2i - j a ij  DS  i  j  n  1
c) A = (aij)2x3, tal que aij = (i + j)2.
Temos para este caso:
2 , se , i  j
d) C = (cij)3x3, tal que c ij   
i  j , se , i  j
Diagonal Principal: D.P = 1, 4, 8 e
 Diagonal Secundária: D.S = 0, 4, 1.
e) D = (dij)2x4, tal que:
 i 2 , se , i  j par Tipos de Matrizes.
d ij  
2i. j , se , i  j ímpar a) Matriz Nula.
Matriz onde todos os elementos são zeros.
Formas de Matrizes.
0 0 0 
De acordo com o número de linhas(m) e de Exemplo: A 
colunas(n), as matrizes recebem nomes especiais. 0 0 0  2 X 3
a) Matriz Retangular.( m  n).
Toda matriz que possui o número de linhas b) Matriz Escalar.
diferentes do número de colunas.
Exemplos: a 0 0 

Exemplo: A  0 a 0
 , onde a  0
 
0 2 0 0 a  3 X 3
2  5 7   3 5   
A  B 
0 1  8 2 X 3  8  5 3 X 2
  c) Matriz Identidade.
Casos Particulares: Matriz escalar onde os elementos da diagonal
principal valem 1.
 Matriz Linha ( 1 X n). Exemplo:
Toda matriz que possui uma única linha.)
Exemplos: 1 0 0
A  0 1 0 
 
A  0  1 5 2 11X 5 0 0 1  3 X 3
 
 Matriz Coluna (n X 1).
Toda matriz que possui uma única coluna d) Matriz Oposta.
Exemplos: Matriz obtida de uma matriz A, trocando-se
todos os sinais de seus elementos.
  2 Exemplo:
A 5 
   1 2
 3 3X 1 Sendo A    , então – A será:
   2 5 2 X 2
b) Matriz Quadrada( m = n).
  1  2
Toda matriz que possui igual número de linhas A 
e colunas.  2  5 2 X 2
Exemplos:
 1 2 0
A    5 4 3
 
 1 2 8 3 X 3
 

3. E.E.B.A.P – 3º Ano Ens. Médio – Matemática - Profº Nélio Nahum 3
e) Matriz Transposta. III. Multiplicação de Escalar por Matriz.
Chamamos de matriz transposta de A, e Dado um número real x e uma matriz A de
T
representamos por A , a matriz obtida de A, através da ordem mXn, o produto de x por A é a matriz, de ordem
troca ordenada de linhas por colunas. mXn, obtida pela multiplicação de todos os elementos
Exemplo: da matriz A por x.
1 5 9  Exemplo:
Sendo A    ,
7 6 3 2 X 3 1 2
Dadas as matrizes: A    e
T
teremos como A a seguinte matriz: 3 5 2 X 2
 1 0
B  ,
1 7  2 4 2 X 2
A  5 6
T
 
Determine:
a) 3.A
9 3 3 X 2
  b) -2.B
f) Matriz Simétrica: 1
T
c) A
É uma matriz quadrada em que A = A . 2
d) 2A + B.
Exemplo:
e) 3.A - B
2 3 5 2 3 5
 3 1 4
A 
e A  3 1 4
T 
  
5 4 7  3 X 3
  5 4 7  3 X 3
  IV. Multiplicação de Matrizes.
Igualdade e Operações com Matrizes. A multiplicação da matriz A = ( aij)mXn, pela
matriz B = ( bij)nXp, que indicamos por A.B, é a matriz
I. Igualdade: obtida pela multiplicação das linhas de A, pelas colunas
de B.
Duas matrizes serão iguais se, possuem a Obs: só será possível multiplicar matrizes, se o
mesma ordem e apresentam elementos número de colunas da primeira for igual ao número de
correspondentes iguais. linhas da segunda.
Exemplo: AmXn X BnXp = (A X B)mXp.
Determine x, y e z, para que as matrizes A e B,
Exemplo:
sejam iguais. 2 1 3
Dadas as matrizes: A    e
 x y 1 0  5 4 6 2 X 3
A  e B   z 2
 5 2  2 x 2   2x2 4 1 
B  2 3 .Calcule se possível:
 
II. Adição e Subtração.
5 2 3 X 2
 
Para somar(ou subtrair) matrizes, basta
somar(ou subtrair) os seus elementos correspondentes. a) A.B
b) B.A
Obs: só podemos somar ou subtrair matrizes c) B
2
se elas forem de mesma ordem. d) A²
Exemplo: Dadas as matrizes:
3 4  2
A  e
1 3 7  2 X 3
1  5 2 
B  , determine:
0 4  7  2 X 3
a) A+B
b) A–B

4. E.E.B.A.P – 3º Ano Ens. Médio – Matemática - Profº Nélio Nahum 4
1 2 m 1
Exercícios. 4ª). Sendo 1 4 . n   5 , determine m + n
    
1ª). Escreva as matrizes a seguir:  1
a) A = (aij)2x2, tal que aij = 2i + j.
 
5ª). Sobre o produto M.N da matriz M  1
 
 1
b) B = (aij)2x3, tal que aij = i - j.  3 x1
c) C = (cij)3x2, tal que: pela matriz N  1 1 11x3 dizemos que:
0 , se , i  j
 ( a ) Não se define
cij  2 , se , i  j ( b ) É a matriz identidade de ordem 3
 1, se , i  j
 ( c ) É a uma matriz quadrada de ordem um.
( d ) É a uma matriz quadrada de ordem 3
d) D = (dij)2x2, tal que: ( e ) É uma matriz retangular 3x1.
6ª). Dada a matriz A (aij)2x2 tal que:
i 2 , se , i  j par
dij  
 j , se , i  j ímpar   
sen i  se i  j
aij    2  , Calcule:
e) A  (aij )3 x 2 , tal que: aij  i  j cos(  . j) se i  j

1, se i = j
f) B  (bij )3 x 2 , tal que bij   a) A
i+j, se i  j b) A
2
0, se i  j 7ª). A matriz C fornece, em reais, o custo das
 porções de arroz, carne e salada usados num
c) B  (bij )3 x 3 , tal que aij  i, se i  j restaurante. A matriz P fornece o número de porções
i  j , se i  j de arroz, carne e salada usados na composição dos
 pratos P1, P1 e P3 desse restaurante.
2ª). Dadas as matrizes:
2 1 1 prato 1
1 arroz
P  1 2 1 prato 2
2 3
A
0 2 3 2 C  3 carne  
 , B  1 3 e C  1 0   2 2 0 prato 3
 
1 0      2 salada
 
A C S
Determine a matriz X, tal que:
Forme a matriz que fornece o custo de
a) X+C =A produção, em reais, dos pratos P1, P1 e P3.
b) X+B=A
8ª). Uma empresa produz certo produto em três
c) 2A = B + X modelos, A, B e C. Cada modelo é parcialmente
d) A+B+X=0 fabricado na fábrica E1 em Castanhal e então concluído
na fábrica E2 em Belém. O custo total de cada produto
consiste no custo de manufatura e no custo de
3ª). Calcule em cada caso A.B, B.A, A e B .
2 2 transporte. Onde os custos em cada fábrica (em reais)
podem ser descritos pelas matrizes E1 e E2.Calcule o
1 1  3 4 custo total de C.
a) A  e B  5 2
 2 0  
32 40 A  40 60 A
 5  2 E1  50 50  B
  E 2   50
 50 B

0 
b) A   1 0  e B   
  70 20 C 130 20 C
1    
0
 3 fabr transp fabr transp