Transformationdelaplace
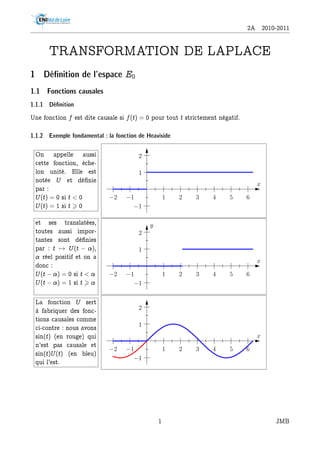
- 1. 2A 2010-2011 TRANSFORMATION DE LAPLACE 1 Dénition de l'espace -0 1.1 Fonctions causales 1.1.1 Dénition Une fonction f est dite causale si f(t) = 0 pour tout t strictement négatif. 1.1.2 Exemple fondamental : la fonction de Heaviside On appelle aussi cette fonction, éche- lon unité. Elle est notée U et dénie par : U(t) = 0 si t 0 U(t) = 1 si t 0 −1 1 2 −2 −1 1 2 3 4 5 6 x et ses translatées, toutes aussi impor- tantes sont dénies par : t 7! U(t ), réel positif et on a donc : U(t ) = 0 si t U(t ) = 1 si t −1 1 2 y −2 −1 1 2 3 4 5 6 x La fonction U sert à fabriquer des fonc- tions causales comme ci-contre : nous avons sin(t) (en rouge) qui n'est pas causale et sin(t)U(t) (en bleu) qui l'est. −1 1 2 −2 −1 1 2 3 4 5 6 x 1 JMB
- 2. 2A 2010-2011 Ici nous avons sin(t)U(t) (en bleu) et sa translatée de qui est donc : sin(t )U(t ) (en rouge) −1 1 2 −2 −1 1 2 3 4 5 6 x 1.2 Les fonctions de - 1.2.1 Dénition E0 est l'ensemble de toutes les combinaisons linéaires à coecients réels ou complexes des fonctions de la forme t 7! U(t )tner t où est un réel positif, n un entier positif et r un nombre complexe quelconque, c'est à dire que E0 est l'ensemble de toutes les fonctions qui peuvent s'écrire comme somme de fonctions du type U(t )tner t avec devant ce genre de fonctions des coecients réels ou complexes. Exemple 1. X la fonction t 7! t2 e tU(t 3) est une fonction de E0 X la fonction t 7! sin(t)U(t) est une fonction de E0. En eet, sin(t)U(t) = 1 2i eitU(t) 1 2i e itU(t). X la fonction t 7! sin(t )U(t ) est une fonction de E0. En eet sin(t )U(t ) = U(t ) ei(t ) e i(t ) 2i # = e i 2i eitU(t ) ei 2i e itU(t ) 1.2.2 Propriétés 1. Toute fonction de E0 est continue par morceaux sur 4 c'est à dire présentant un nombre ni de discontinuité de 1ère espèce. 2. Si et
- 3. sont des réels positifs, r un nombre complexe et f une fonction appartenant à E0, alors les fonctions t 7! f(t); t 7! f(t
- 4. ) et t 7! er tf(t) appartiennent aussi à E0: 3. Soit f une fonction appartenant à E0 alors f et Z t 0 f(x)dx appartiennent aussi à E0: Exemple 2. 2 JMB
- 5. 2A 2010-2011 La fonction dénie par : f(t) = tU(t) 2(t 1)U(t 1) + (t 2)U(t 2) appartient à E0. Sa représenta- tion graphique est : 1 y −1 1 2 3 x Exemple 3. La fonction dénie par : g(t) = U(t) 2U(t 1) + U(t 2) appartient à E0. Sa représenta- tion graphique est : ı −1 1 y −1 1 2 3 4 x O 2 Transformation de Laplace dans -0 2.1 Propriété fondamentale 2.1.1 Dénition Si une fonction g est de la forme t 7! g(t) = kU(t )tner t, c'est à dire que c'est l'un des morceaux d'une fonction f appartenant à E0, alors le réel r est appelé exposant de la fonction g. 2.1.2 Propriété Soit f une fonction appartenant à E0, l'intégrale Z + 0 f(t)e ptdt est absolument convergente si p est un nombre réel appartenant à l'intervalle ](f); +1[ où (f) est la plus grande des parties réelles des exposants des fonctions composants f. Le réel (f) est appelé abscisse de convergence de la fonction f. Exemple 4. Soit f la fonction dénie par : f(t) = e2t cos(3t)U(t) + tet sin(t)U(t ) f est bien une fonction de E0 car c'est une combinaison linéaire de fonction du type t 7! U(t )tner t. En eet on peut écrire f(t) = 1 2 U(t)e(2+3i)t + 1 2 U(t)e(2 3i)t + 1 2i tU(t )e(1+i)t 1 2i tU(t )e(1 i)t: Les exposants des fonctions qui composent cette combinaison linéaire sont donc respective- ment : 2 + 3i;2 3i;1 + i;1 i. Les parties réelles sont donc 2 et 1, donc d'après la propriété ci dessus, on sait que Z + 0 f(t)e ptdt converge si le réel p 2 ]2; +1[ 3 JMB
- 6. 2A 2010-2011 2.2 Dénition de la transformée de Laplace Soit f une fonction appartenant à E0 d'abscisse de convergence (f). La transformée de Laplace de f , notée F, est la fonction dénie sur ](f); +1[ par : F(p) = Z + 0 f(t)e ptdt Elle est notée : F = L(f) ou F(p) = L(f) (p) En théorie, on est donc censé, avant de calculer la transformée de Laplace d'une fonction f causale, vérier que f 2 E0 et calculer son abscisse de convergence (f). Dans la pratique, toutes les fonctions que nous manipulons dans ce chapitre appartiennent à E0 et leur abscisse de convergence en général est égale à 0. Néanmoins, il est naturel d'avoir cette rigueur de vérication, au cas où les calculs nous emmènent dans un espace plus compliqué! 2.3 Transformée de Laplace de l'échelon unité L(U(t)) = Z + 0 U(t)e ptdt = Z + 0 e ptdt = – 1 p e pt ™+ 0 = 0 ‚ 1 p Œ = 1 p si p 0: D'où : L(U(t)) = 1 p si p 0 2.4 Transformée de Laplace de B(J) = Jn7(J) F(p) = Z + 0 tnU(t)e ptdt = Z + 0 tne ptdt = In En intégrant par partie, on obtient que In = n p In 1 Or I0 = Z + 0 U(t)e ptdt = 1 p I1 = 1 p I0 = 1 p2 I2 = 2 p I1 = 2 p 1 p2 I3 = 3 p I2 = 3 p 2 p 1 p2 d'où : L(tnU(t)) = n! pn+1 si p 0 2.5 Transformée de Laplace de B(J) = Art7(J) F(p) = Z + 0 ertU(t)e pt = Z + 0 e(r p)tdt. Cette intégrale est convergente si p e(r): On a alors : Z + 0 e(r p)tdt = – 1 r p e(r p)t ™+ 0 = 0 1 r p = 1 p r . D'où L(ertU(t)) = 1 p r si p e(r) 4 JMB
- 7. 2A 2010-2011 2.6 Transformée de Laplace de B(J) = JArt7(J) F(p) = Z + 0 tertU(t)e pt = Z + 0 te(r p)tdt. Cette intégrale est convergente si p e(r): On a alors, en intégrant par parties : L(tertU(t)) = 1 (p r) 2 si p e(r) 2.7 Propriétés de la transformation de Laplace On suppose à partir dans tout ce paragraphe que p appartient à l'intervalle ](f); +1[ ](g); +1[ 2.7.1 Linéarité Si f et g sont des fonctions appartenant à E0 de transformées de Laplace respectives F et G et si et
- 8. sont des nombres complexes quelconques alors si on note H la transformée de Laplace de h = f +
- 9. g : L(f +
- 10. g) = L(f) +
- 11. L(g) H = f +
- 12. g Déterminons les transformées de Laplace des fonctions f(t) = sin(t)U(t) et g(t) = cos(t)U(t) Posons h1(t) = eitU(t) et h2(t) = e itU(t) On a alors d'après Ÿ2.5 : H1(p) = L(h1(t)) = 1 p i et H2(p) = L(h2(t)) = 1 p + i Comme sin(t)U(t) = 1 2i h1(t) 1 2i h2(t) alors L(sin(t)U(t)) = 1 2i 1 p i 1 2i 1 p + i = 1 2 i p + i 1 2 i p i = 1 p2 + 1 Comme cos(t)U(t) = 1 2 h1(t) + 1 2 h2(t) alors L(cos(t)U(t)) = 1 2 1 p i + 1 2 1 p + i = p p2 + 1 L(sin(t)U(t)) = 1 p2 + 1 L(cos(t)U(t)) = p p2 + 1 8p 0 2.7.2 Transformée de Laplace d'une dilatée : t 7! f(at) a 2 4+ Soit f une fonction appartenant à E0 et soit F = L(f) alors L(f(at)) = 1 a F p a ‹ Démonstration : soit Z A 0 f(at)e ptdt 5 JMB
- 13. 2A 2010-2011 En posant u = at on obtient : Z A 0 f(at)e ptdt = 1 a Z aA 0 f(u)e p a udu !A+ 1 a Z + 0 f(u)e p a udu = 1 a F p a ‹ Soit h la fonction de E0dénie par h(t) = cos (!t) U(t) avec ! 0. Soit f la fonction de E0dénie par f(t) = cos (t) U(t) Alors f (!t) = cos (!t) U(!t) = cos (!t) U(t) = h(t) car ! 0 Or L(cos(t)U(t)) = p p2 + 1 Donc L(h(t)) = L(cos (!t) U(t)) = H(p) = 1 ! p ! €p ! Š2 + 1 = p p2 + !2 De la même façon on obtient : L(sin (!t) U(t)) = ! p2 + !2 2.7.3 Transformée de Laplace d'une translatée : t 7! f(t ) avec 2 4+ Soit f une fonction appartenant à E0 et soit F = L(f) alors L(f(t )) = e pF(p) Le terme e p s'appelle le facteur de retard. En clair, lorsqu'une fonction est retardée d'un instant sa transformée de Laplace est mul- tipliée par e p. La démonstration de cette formule est la même que celle ci-dessus en eectuant le changement de variable u = t . On se propose de chercher la transformée de Laplace du signal ci-dessous : −1 1 2 −1 1 2 3 t Appelons f(t) ce signal. On peut alors écrire que : f(t) = tU(t) tU(t 1) + U(t 1) U(t 2) = tU(t) (t 1)U(t 1) U(t 1) + U(t 1) U(t 2) = tU(t) (t 1)U(t 1) U(t 2) donc 6 JMB
- 14. 2A 2010-2011 L(f(t)) = L(tU(t) (t 1)U(t 1) U(t 2)) = L(tU(t)) L((t 1)U(t 1)) L(U(t 2)) = 1 p2 1 p2 e p 1 p e 2p 2.7.4 Multiplication par la variable Soit f une fonction appartenant à E0 et soit F = L(f) alors L( tf(t)) = dF dp (p) L(( t) nf(t)) = dnF dpn (p) Soit f(t) = tsin(!t)U(t). On sait que la transformée de Laplace de sin(!t)U(t) est : L(sin(!t)U(t)) = ! p2 + !2 . Or d dp – ! p2 + !2 ™ = 2p ! (p2 + !2 ) 2 # donc L(tsin(!t)U(t)) = 2p ! (p2 + !2 ) 2 2.7.5 Multiplication par e at où a est un réel quelconque Soit f une fonction appartenant à E0 et soit F = L(f) alors L € f(t)e at Š = F(p + a) Soit f la fonction dénie par : f(t) = e at cos(!t)U(t): Nous savons que L(cos(!t)U(t)) = p p2 + !2 = F(p) Donc : L € e at cos(!t)U(t) Š = F(p + a) = p + a (p + a) 2 + !2 . 2.7.6 Transformée de Laplace d'une dérivée Soit f une fonction appartenant à E0 et soit F = L(f) alors si f est continue sur l'intervalle ]0; +1[ L(f(t)) = pF(p) f(0 + ) où f(0 + ) = lim t0+f(t) de même si de plus f est continue sur l'intervalle ]0; +1[ alors : L(f(t)) = p2 F(p) pf(0 + ) f(0 + ) où f(0 + ) = lim t0+f(t) 7 JMB
- 15. 2A 2010-2011 Soit f(t) = cos(!t)U(t) alors f(t) = ! sin(!t)U(t) + cos(!t)U(t) Or U(t) = 0 sur l'intervalle ]0; +1[ Donc : f(t) = ! sin(!t)U(t) sur l'intervalle ]0; +1[ Donc L(f(t)) = p p p2 + !2 cos(0) = p p p2 + !2 1 = p2 p2 + !2 1 = !2 p2 + !2 c'est à dire L( ! sin(!t)U(t)) = !2 p2 + !2 donc on retrouve que L(sin(!t)U(t)) = ! p2 + !2 Soit f la fonction représentée par le graphe ci-dessous : ı −1 1 y −1 1 2 3 4 x O On a donc f(t) = U(t) U(t 1) + ( t + 2)U(t 1) ( t + 2)U(t 2) c'est à dire que f(t) = U(t) + ( t + 1)U(t 1) + (t 2)U(t 2) f(t) = U(t) (t 1)U(t 1) + (t 2)U(t 2) donc L(f(t)) = 1 p 1 p2 e p + 1 p2 e 2p = F(p). Soit maintenant g la fonction dont le graphe est donné ci-dessous : ı −1 1 y −1 1 2 3 4 x O On a donc g(t) = (U(t 1) U(t 2)) = U(t 1) + U(t 2) Or, on a f(t) = g(t): Donc L(f(t)) = L(g(t)) = pF(p) f(0 + ) = p – 1 p 1 p2 e p + 1 p2 e 2p ™ 1 = 1 p e p + 1 p e 2p Le calcul direct nous donne : L (g(t)) = 1 p e p + 1 p e 2p qui redonne la même transformée de Laplace! 8 JMB
- 16. 2A 2010-2011 2.8 Théorème de la valeur initiale et de la valeur nale 2.8.1 Théorème de la valeur initiale Si une fonction f appartenant à l'ensemble E0 admet pour transformée de Laplace la fonction F, alors lim p+F(p) = 0 lim p+pF(p) = f(0 + ) 2.8.2 Théorème de la valeur nale Si une fonction f appartenant à l'ensemble E0 admet pour transformée de Laplace la fonction F et si lim t+ f(t) existe et est nie, alors : lim p0 pF(p) = lim t+ f(t) Soit g(t) = (cos t) U(t) alors L(g(t)) = G(p) = p p2 + 1 lim p+pG(p) = lim p+ p2 p2 + 1 = 1 = g(0 + ) = cos 0 ce qui vérie le théorème de la valeur initiale lim p0 pF(p) = 0 = lim t+ (cos t) U(t) cette limite n'existe pas , le théorème de la valeur nale ne s'applique pas. 3 Produit de convolution dans -0 3.1 Dénition On rappelle que le produit de convolution de deux fonctions f et g est une fonction h dénie ci-dessous. Ce produit est noté . On a : h(t) = (f g) (t) = Z + f(x)g(t x)dx Si f est causale, l'intégrale devient : h(t) = (f g) (t) = Z + 0 f(x)g(t x)dx Si de plus g est causale alors la fonction h l'est aussi et on a : h(t) = 0 si t 0 h(t) = Z t 0 f(x)g(t x)dx si t 0 9 JMB
- 17. 2A 2010-2011 D'où la dénition suivante : Soient f et g deux fonctions appartenant à E0:On appelle convolée des fonctions f et g dans cet ordre, la fonction causale h dénie pour tout t positif par : h(t) = (f g) (t) = Z t 0 f(x)g(t x)dx 3.2 Propriétés du produit de convolution Le produit de convolution est commutatif, associatif et distributif par rapport à l'addition. De plus le produit de convolution est une loi dite interne, c'est à dire que l'on a : X f g = g f X (f g) h = f (g h) X Si f et g appartiennent toutes deux à E0 alors h = f g appartient aussi à E0: (démonstrations laissées au lecteur!) 3.3 Transformée de Laplace d'un produit de convolution Si f et g appartiennent toutes deux à E0 alors la convolée h = f g a pour transformée de Laplace le produit des transformée de Laplace de f et g, c'est à dire que l'on a : L(f g) = L(f) L(g) Cette propriété nous permettra d'obtenir la transformée de Laplace de fonctions qu'on ne peut calculer grâce aux propriétés déjà vues dans le paragraphe 2.7. 3.4 Transformée de Laplace de Z x B(J)@J Soit f une fonction appartenant à l'ensemble E0 et U la fonction échelon unité alors on a : 8x 0 (U f) (x) = Z x 0 f(t)U(x t)dt = Z x 0 f(t)dt Si on note F = L(f(t)) et en rappelant que L(U(t)) = 1 p , alors en utilisant le théorème ci dessus on obtient : L Z x 0 f(t)dt ‹ = F(p) p 10 JMB
- 18. 2A 2010-2011 4 Transformée de Laplace de l'impulsion unité On considère la fonction fn dénie par : fn(t) = n si 0 6 t 6 1 n et fn(t) = 0 sinon dont voici la représentation graphique ci-contre pour quelques n = 1, 2 et 4. Si on note Fn(p) = L(fn(t)) et en remarquant que fn(t) = nU(t) nU(t 1 n ) alors on a Fn(p) = n p n p e p n ı 1 2 3 4 y −1 1 2 x O Maintenant si on fait tendre n ! +1, alors on obtient une pseudo fonction, qui est en fait ce qu'on appelle en mathématiques une distribution, mais qui n'est plus une fonction, qu'on appelle im- pulsion unité ou plus simplement Dirac, impossible à représenter, si ce n'est en faisant un schéma que tous les électroniciens uti- lisent : Cette distribution est notée et on a : L((t)) = lim n+Fn(p) = lim n+ n p n p e p n = 1 5 Transformation de Laplace des fonctions périodiques Soit f une fonction T-périodique, causale, n'appartenant pas forcément à E0: Soit f0 la fonction dénie par : f0(t) = f(t) si 0 t T et f0(t) = 0 sinon telle que f0 appartiennent à E0 alors on a : L(f(t)) = L(f0(t)) 1 e pT Exemple 5. Déterminer la transformée de Laplace de la fonction f T- périodique, causale, dénie sur [0; T[ par f(t) = t. f0(t) = tU(t) tU(t T) = tU(t) (t T)U(t T) TU(t T) donc L(f0(t)) = 1 p2 1 p2 e pT T 1 p e pT et donc L(f(t)) = 1 p2 1 p2 e pT T 1 pe pT 1 e pT ı 1 2 3 4 y −1 1 2 3 4 x O Exemple 6. Le train d'impulsion Cela correspond, en électronique à des ashs éclairs périodiques. alors on a L(f(t)) = 1 1 e pT car L((t)) = 1 11 JMB
- 19. 2A 2010-2011 6 Table des transformées de Laplace On note F(p) = L(f(t)) où f est une fonction appartenant à E0 L((t)) 1 L(U(t)) 1 p L(tU(t)) 1 p2 L(tnU(t)) n! pn+1 L € e atU(t) Š 1 p + a L € te atU(t) Š 1 (p + a) 2 L € tne atU(t) Š n! (p + a) n+1 L(cos (!t) U(t)) p p2 + !2 L(sin (!t) U(t)) ! p2 + !2 L(f(t a)U(t a)) e apF(p) L € e atf(t) Š F(p + a) L(f(t)) pF(p) f(0 + ) L Z t 0 f(u)du F(p) p L(tf(t)) F(p) L(f(t)) p2 F(p) pf(0 + ) f(0 + ) L ‚ f(t) t Œ Z + p F(u)du Pour f T-périodique : L(f(t)) F0(p) 1 e pT où F0(p) = L(f0(t)) 7 Transformée de Laplace inverse La transformée de Laplace étant un opérateur bijectif, sa bijection inverse existe. Elle est unique et on l'appelle original de F ; on a alors : L 1 (F(p)) = f(t): Cela signie que connais- sant la transformée de Laplace d'un signal, on retrouve, grâce à une lecture dans l'autre sens dans la table des transformées de Laplace, le signal. 7.1 Linéarité de la transformation de Laplace inverse Soient F(p) = L(f(t)) et G(p) = L(g(t)), f et g étant deux fonctions appartenant à E0. Soient et deux réels quelconques alors : 12 JMB
- 20. 2A 2010-2011 L 1 [F(p) + G(p)] = L 1 [F(p)] + L 1 [G(p)] Cette propriété conduit, pour la recherche d'un signal dont on connait l'original, à transformer celui-ci en une somme d'éléments simples dont on peut facilement retrouver les originaux grâce à la lecture en sens inverse dans la table. 7.2 Processus à suivre pour la transformation de F(p) en somme d'éléments simples 1. s'il y a des retards, les traiter en premier, séparément. 2. pour des fractions rationnelles du genre F(p) = P(p) Q(p) avec deg P deg Q, on décompose dans 4 cette fraction en éléments simples. Les éléments simples de première espèce se traitent facilement. Pour ceux de seconde espèce, on doit mettre leur dénominateur sous forme canonique, pour retrouver des originaux en cosinus ou en sinus. Exemple 7. Trouver l'original de F(p) = 1 e 2p p2 + 3p + 2 F(p) = 1 e 2p p2 + 3p + 2 = 1 p2 + 3p + 2 e 2p p2 + 3p + 2 = ‚ 1 p + 1 1 p + 2 Œ e 2p ‚ 1 p + 1 1 p + 2 Œ d'où f(t) = € e t e 2t Š U(t) € e (t 2) e 2(t 2) Š U(t 2) Exemple 8. Trouver l'original de F(p) = 1 (p + 1) (p2 + 2p + 2) F(p) = 1 (p + 1) (p2 + 2p + 2) = 1 p + 1 p + 1 (p + 1) 2 + 1 d'où f(t) = e tU(t) e t (cos t) U(t) 7.3 Propriétés de la transformée de Laplace inverse Soit f une fonction appartenant à l'ensemble E0 et dont la transformée de Laplace est F(p). 1. L 1 [F(p)] = tf(t) 2. L 1 Z + p F(u)du = f(t) t 13 JMB
- 21. 2A 2010-2011 8 Résolution des équations diérentielles grâce à la transformée de Laplace 8.1 Équations diérentielles linéaires du premier ordre à coecients constants On considère l'équation diérentielle suivante : (E) : y(t) + ay(t) = f(t) où a est un réel quelconque, f une fonction appartenant à l'ensemble E0 et y une fonction appartenant aussi à E0. On note F(p) = L(f(t)) et Y (p) = L(y(t)) En appliquant à l'équation (E), la transformation de Laplace on a alors : L(y(t) + ay(t)) = L(f(t)) , L(y(t)) + aL(y(t)) = L(f(t)) , pY (p) y(0 + ) + aY (p) = F(p) d'où : Y (p) = F(p) + y(0 + ) p + a puis grâce à la transformée de Laplace inverse, on recherche l'original de Y (p) c'est à dire L 1 [Y (p)] = y(t). 8.2 Équations diérentielles linéaires du second ordre à coecients constants On considère l'équation diérentielle suivante : (E) : y(t) + ay(t) + by(t) = f(t) où a et b sont des réels quelconques, f une fonction appartenant à l'ensemble E0 et y une fonction appartenant aussi à E0. On note F(p) = L(f(t)) et Y (p) = L(y(t)) En appliquant à l'équation (E), la transformation de Laplace on a alors : L(y(t) + ay(t) + by(t)) = L(f(t)) , p2 Y (p) py(0 + ) y(0 + )+a € pY (p) y(0 + ) Š +bY (p) = F(p) d'où : Y (p) = F(p) + py(0 + ) + ay(0 + ) + y(0 + ) p2 + ap + b puis grâce à la transformée de Laplace inverse, on recherche l'original de Y (p) c'est à dire L 1 [Y (p)] = y(t). Exemple 9. Résoudre l'équation diérentielle y(t) + 6y(t) + 9y(t) = t2 e 3t sachant que y(0) = et y(0) =
- 22. F(p) = L € t2 e 3t Š = 2 (p + 3) 3 d'où : Y (p) = 2 (p+3)3 + p + 6 +
- 23. p2 + 6p + 9 = 2 (p + 3) 5 + p + 3 (p + 3) 2 +
- 24. + 3 (p + 3) 2 = 2 (p + 3) 5 + p + 3 +
- 25. + 3 (p + 3) 2 d'où : y(t) = 1 12 t4 e 3t + e 3t + (3 +
- 26. ) te 3t U(t) 14 JMB
- 27. 2A 2010-2011 8.3 Résolution des systèmes diérentielles d'ordre 1 La méthode consiste simplement à eectuer la transformation de Laplace de chacune des équations du système, qui sont du premier ordre. On aboutit ainsi à un système linéaire de n équations à n inconnues : Y1(p); Y2(p); :::;Yn(p), dans lesquelles p joue le rôle d'un paramètre. Puis par recherche des originaux de chacune des Y1(p); Y2(p); :::;Yn(p), on retrouve la solution du système diérentiel de départ. 15 JMB
- 28. 2A 2010-2011 9 EXERCICES 9.1 Calcul de transformées de Laplace directes Exercice 1. 1. Linéariser en utilisant une formule trigonométrique : f(t) = cos 2 (!t) 2. En déduire, en vous aidant des propriétés classiques et du formulaire, la transformée de Laplace de f(t) = cos 2 (!t)U(t) Exercice 2. Calculer la transformée de Laplace du signal ci-dessous : ½ ½ ¾ ¿¹½ Ç Exercice 3. Calculer, à partir de la dénition, la transformée de Laplace du signal réel ci-dessous : (V0 0 et 0) ½ ¾ ¿¹½ ½ ¾ ¿ Ç Î¼ Retrouver le résultat précédent en décomposant le signal en une combinaison linéaire de signaux élémentaires et en utilisant le formulaire. Exercice 4. Calculer la transformée de Laplace du signal suivant (méthode au choix) : ½ ¾ ¿¹½ ½ ¾ ¿ Ç Î¼ ¾ Exercice 5. Calculer la transformée de Laplace du signal suivant (méthode du formulaire) : 16 JMB
- 29. 2A 2010-2011 ½ ¾ ¿¹½ ½ ¾ ¿ ¹½ ¹¾ ¹¿ Ç Î¼ ¾ μ Exercice 6. Trouver les transformées de Laplace des signaux f1 et f2suivants et les représenter graphiquement : f1(t) = ( sin t si 0 6 t 6 0 si t ou t 0 ; f2(t) = ( 1 si 0 6 t 6 a 0 si t a ou t 0 Exercice 7. Calculer les transformées de Laplace des signaux T périodiques dénis ci-dessous : 1. f(t) = jsin tjU(t) 2. f(t) = 8 : 1 si 0 t a 0 si a 6 t 6 2a T = 2a 9.2 Calculs de transformées de Laplace inverses. Exercice 8. Calculer L 1 ‚ 11p + 1 (p + 1) (p2 + 4) Œ Exercice 9. Trouver f(t) sachant que F(p) = 1 (p 1)(p2 + 1) Exercice 10. Calculer L 1 ‚ 14p2 + 55p + 51 2p3 + 12p2 + 22p + 12 Œ Exercice 11. Trouver f(t) sachant que : F(p) = 1 + e p p2 + 1 et représenter graphiquement f(t). Exercice 12. Trouver f(t) sachant que : F(p) = 1 p(p + 2) 3 (p + 3) 17 JMB
- 30. 2A 2010-2011 9.3 Application de la transformée de Laplace à la résolution d'équations diéren- tielles. Exercice 13. En utilisant la transformée de Laplace, résoudre l'équation diérentielle suivante y(4) (t) + 5y(t) + 4y(t) = sin t et t 0; y(0) = y(0) = y(0) = y(0) = y(4) (0) = 0 Exercice 14. En utilisant la transformée de Laplace, résoudre l'équation diérentielle suivante y(t) y(t) + y(t) = (t 1)etU(t) et y(0) = 0;y(0) = 1 Exercice 15. En utilisant la transformée de Laplace, résoudre l'équation diérentielle suivante ty(t) y(t) + ty(t) y(t) = 0 et y(0) = y(0) = y(0) = 0 et y(0) = 1: 9.4 Application de la transformée de Laplace à la résolution de systèmes diérentiels. Exercice 16. Résoudre 8 : x(t) = 2y(t) + 2z(t) y(t) = 2x0(t) z(t) z(t) = 2x(t) + y(t) x(0) = 1; y(0) = z(0) = 0 18 JMB