Potências: conceitos e propriedades
•Transferir como PPT, PDF•
4 gostaram•4,445 visualizações
1) Potenciações representam multiplicações repetidas onde os fatores são iguais. 2) Uma potência é representada por baseelevadoaexpoente, onde a base é o fator e o expoente indica a quantidade de vezes que a base é multiplicada. 3) Existem propriedades para cálculo de potenciações, como somar expoentes para multiplicação de bases iguais e distribuir potências em produtos.
Denunciar
Compartilhar
Denunciar
Compartilhar
Mais conteúdo relacionado
Mais procurados
Mais procurados (20)
www.AulasDeMatematicaApoio.com - Matemática - Potenciação

www.AulasDeMatematicaApoio.com - Matemática - Potenciação
Grandezas diretamente e inversamente proporcionais

Grandezas diretamente e inversamente proporcionais
Destaque
Destaque (20)
GINCANA MATEMÁTICA RADICIAÇÃO, POTENCIAÇÃO E NOTAÇÃO CIENTÍFICA.

GINCANA MATEMÁTICA RADICIAÇÃO, POTENCIAÇÃO E NOTAÇÃO CIENTÍFICA.
www.CentroApoio.com - Matemática - Radiciação - Vídeo Aulas 

www.CentroApoio.com - Matemática - Radiciação - Vídeo Aulas
Semelhante a Potências: conceitos e propriedades
Semelhante a Potências: conceitos e propriedades (20)
POTENCIA-2018 (1).pptxpotenciapotenciapotenciapotencia

POTENCIA-2018 (1).pptxpotenciapotenciapotenciapotencia
www.AulasDeMatematicanoRJ.Com.Br - Matemática - Potenciação

www.AulasDeMatematicanoRJ.Com.Br - Matemática - Potenciação
www.AulasDeMatematicaApoio.com.br - Matemática - Potenciação

www.AulasDeMatematicaApoio.com.br - Matemática - Potenciação
Mais de leilamaluf
Mais de leilamaluf (20)
Potências: conceitos e propriedades
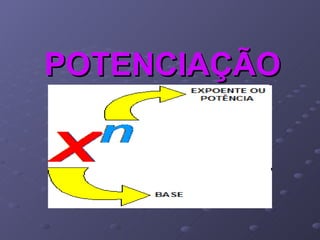
- 1. POTENCIAÇÃO