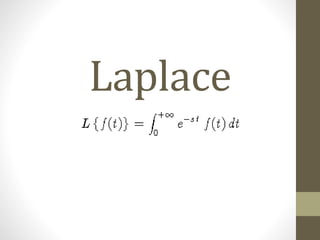
Matemática Superior Para Ingenieros: Laplace
- 1. Laplace
- 2. Pierre Simon Marquéz de Laplace • Laplace(1749-1827), astrónomo y matemático francés, "el Newton de Francia”. • Conocido por haber aplicado con éxito la teoría de la gravitación de Newton a los movimientos planetarios en el Sistema Solar. En 1767 fue profesor de matemáticas en la Escuela Militar de París y en 1785 fue elegido miembro de la Academia de Ciencias Francesa. • Laplace realizó su trabajo más importante al desarrollar el análisis matemático del sistema de astronomía gravitacional elaborado por el matemático, físico y astrónomo británico Isaac Newton. • Demostró que los movimientos planetarios son estables y que las perturbaciones producidas por la influencia mutua de los planetas o por cuerpos externos, como los cometas, solamente son temporales. • En Mecánica celeste (5 volúmenes, 1799-1825) Laplace sistematizó toda la obra matemática que se había realizado sobre la gravitación. • Exposición del sistema del mundo (1796) contiene un resumen de la historia de la astronomía. • Trabajó sobre la teoría de la probabilidad en su Teoría analítica de las probabilidades (1812) • Ensayo filosófico sobre la probabilidad. (1814).
- 3. Transformada de Laplace Proporciona una alternativa mas sistemática para la investigación de ecuaciones diferenciales que el método propuesto por heaviside l{f (t)}= F(s) l{f (t)} = -st e f (t)dt 0 ¥ ò
- 4. La propiedad de linealidad Si f(t) y g(t) son funciones que tienen transformadas de Laplace si a y b son constantes cualesquiera entonces L af (t)+bg(t){ }= aL f (t){ }+bL g(t){ } Ejemplo L 3t + 2 3t e{ } = L 3t{ } + L 2 3t e{ } = 3L t{ } + 2L 3t e{ } = 3 2 s + 3 s - 3
- 5. Primer teorema de traslación L at e f (t){ }= F(s-a) L at e f (t){ }= L s®s-a f(t){ } L f (t){ }= -st e f (t)dt = F(s) 0 ¥ ò L at e f (t){ }= F(s - a) L at e f (t){ }= -st e at e f (t)dt 0 ¥ ò = (-s+a)t e f (t)dt 0 ¥ ò = -(s-a)t e f (t)dt 0 ¥ ò
- 6. Ejemplos L 2t e 3 t{ } = L s®s-a 3 t{ } = 3! s®s-a 4 s = 3! 4 s-2( ) L -3t e sen2t{ } = 2 s®(s+3) 2 s + 2 2 = 2 2 s+3( ) + 4
- 7. Derivada de la transformada L n t f (t){ }= n (-1) n d F(s) n ds
- 8. Ejemplo L 2 t t e{ } L t e{ }= F(s) = 1 s -1 = L 2 t t e{ }= 2 (-1) 2 d F(S) 2 ds = 2 (-1) 2 d 2 ds 1 s -1 æ è ç ö ø ÷ = (-1) d ds 1 2 (s-1) æ è ç ç ö ø ÷ ÷ = 2 3 (s-1) Escogemos cual será nuestra f(t) Así, por el teorema de derivada
- 9. Ejemplo L -t te cost{ }= -1( ) d ds L -t e cost{ } = (-1) d ds s®(s+1) s 2 s +1 æ è ç ö ø ÷ = - d ds s+1 2 s+1( ) +1 æ è ç ç ç ö ø ÷ ÷ ÷ = - 1- 2 (s+1) 2 2 (s+1) +1é ë ù û
- 10. Transformada de una derivada Hasta una unidad menos de la función menos que estoy derivado L n t (t){ }= n s F(s)- n-1 s f (0)- n-2 s f '(0)- n-3 s f ''(0)
- 11. k = k s tn = n!/ s(n+1) eaat = 1 s - a coskt = s s2 + k2 senkt = k s2 + k2 senhkt = k s2 - k2 coshkt = s s2 - k2 Uso de Tabla para encontrar la transformada de Laplace L et senh2t{ }= senht = et - e-t 2 L{et ( e2t - e-2t 2 )} = L{ e3t 2 - e-t 2 } = 1 2 L{e3t } - 1 2 L{e-t } = 1 2 ( 1 s - 3 )- 1 2 ( 1 s +1 ) = 1 2 1 s - 3 - 1 s +1 æ èç ö ø÷ Ejemplo 1 L cos2 t{ } cos2 x = cos2x+1 2 = L{ cos2t 2 + 1 2 }= 1 2 L{cos2t}+ L{ 1 2 } 1 2 ( s s2 +22 )+ 1 2 s = 1 2 s s2 +4 + 1 s æ èç ö ø÷ Ejemplo 2 L{(t +1)2 } L{t2 +2t +1} = L{t2 }+ L{2t}+ L{1}= 2 s3 + 2 s2 + 1 s = 2+2s+ s2 s3 Ejemplo 3
- 12. Transformada Inversa de Laplace L-1 ( 1 (s - 3)2 ) = e3t × L-1 1 s2 æ èç ö ø÷ = tn = n! s(n+1) ® L-1 n! s(n+1) æ èç ö ø÷ = tn 1 2! L-1 2! s2+1 = t2 = e3t × t2 2 Primer Teorema de Traslación Ejemplo 1 L eat × f (t){ }= F(s - a)® L-1 F(s - a) = eat L-1 F(s) L-1 1 s2 + s +1 ì í î ü ý þ = s2 + s +1= s2 + s +1+ 1 4 - 1 4 = L-1 1 (s + 1 2)2 + 3 4 ì í ï îï ü ý ï þï = e - 1 2 t L-1 1 s2 + 3 4 ì í ï îï ü ý ï þï L-1 k s2 + k2 æ èç ö ø÷ = senkt = e - 1 2 t × 1 3 2 L-1 3 2 s2 + 3 4 æ è ç ç ö ø ÷ ÷ = e -1 2t 2 3 sen 3 2 t Ejemplo 2
- 13. Transformada Inversa de Laplace Fracciones Parciales Ejemplo 1 L-1 1 s2 + 3s ì í î ü ý þ = L-1 1 s(s + 3) ì í î ü ý þ A s + B s + 3 = 1 s(s + 3) A(s + 3)+ Bs = 1 (A + B)s + 3A = 1 A + B = 0 3A = 1 A = 1 3 1 3 + B = 0 B = - 1 3 1 s(s + 3) = 1 3 s - 1 3 s + 3 L-1 1 3 s - 1 3 s + 3 ì í ï îï ü ý ï þï = L-1 1 3 s ì í ï îï ü ý ï þï - 1 3 L-1 1 s + 3 ì í î ü ý þ = 1 3 - 1 3e-3t El método de las fracciones parciales consiste en descomponer un cociente de polinomios en una suma de fracciones de polinomios de menor grado. El grado del polinomio del denominador debe ser estrictamente mayor que el del numerador.
- 14. L-1 s (s2 + 4)(s+2) ì í î ü ý þ = s (s2 + 4)(s+ 2) = As+ B s2 + 4 + C s+2 s = (As+ B)(s+ 2)+C(s2 + 4) s = As2 +2As+ Bs+ 2B+Cs2 + 4C s = (A+C)s2 +(2A+ B)s+(2B+ 4C) A+C = 0 2A+ B =1 2B+ 4C = 0 -4A+2B = 0 2A + B = 1 B = 2A 2A + 2A =1 4A = 1 A = 1 4 B = 1 2 C = - 1 4 = L-1 1 4 s s2 + 4 + 1 2 s2 + 4 - 1 4 s + 2 ì í ï îï ü ý ï þï = 1 4 L-1 s s2 + 4 ì í î ü ý þ + 1 2 × 1 2 L-1 2 s2 + 4 ì í î ü ý þ - 1 4 1 s + 2 ì í î ü ý þ = 1 4 cos2t + 1 4 sen2t - 1 4 e-2t = 1 4 cos2t + sen2t - e-2t ( ) Ejemplo 2
- 15. Transformada de Laplace de una Integral L-1 1 s(s2 +1) ì í î ü ý þ F(s) = 1 s2 +1 L-1 F(s) s æ èç ö ø÷ = f (t )dt 0 t ò = L-1 (F(s)dtt®t = (L-1 1 s2 +10 t ò )dtt®t = sent[ ] 0 t ò t®t dt = -cost0 t = -cost - (-1) = -cost +1 L-1 1 s(s -1) ì í î ü ý þ F(s) = 1 s -1 = (L-1 1 s -1 ) 0 t ò dtt®t = et éë ùû 0 t ò t®t dt = et = et - e0 = et -1 L f t( )dt 0 t ò ì í î ü ý þ = F(s) s L-1 F(s) s æ èç ö ø÷ = f (t )dt 0 t ò Ejemplo 2Ejemplo 1
- 16. Teorema de Convolución L f * g{ } = L f (t){ }× L g(t)( ) = F(s)×G(s) L-1 F(s)×G(s){ } = f * g f * g = g * f f (t) = et g(t) = t = et (t -t )dt 0 t ò = (et t -tet 0 t ò )dt = t et 0 t ò dt - tet dt 0 t ò = tet - (et t - et )0 t = tet - te0 éë ùû - (et t - et + e0 ) = tet - t - et t - et -1 = et - t -1 Ejemplo 1: convolucion de dos funciones f *g = f (t)g(t -t)dt 0 t ò L et sen(t -t )dt 0 t ò ì í î ü ý þ f (t) = et g(t) = sent L et *sent{ }= L et { }× L sent{ } = 1 s -1 × 1 s2 +1 Ejemplo 2: Transformada de una convolucion
- 17. Ejemplo 3: Inversa de productos de dos funciones en s, usando la convolucion. L-1 1 (s -1)(s + 4) ì í î ü ý þ = L-1 1 s -1 × 1 s + 4 ì í î ü ý þ L-1 F(s)×G(s){ }= f (t)*g(t) F(s) = 1 s -1 ® f (t) = et G(s) = 1 s + 4 ® g(t) = e-4t et e-4(t-t ) dt = et e-4t e4t 0 t ò0 t ò dt = e-4t e5t dt 0 t ò = e-4t e5t 5 é ë ê ù û ú 0 t = e-4t e5t 5 - 1 5 é ë ê ù û ú = et 5 - e-4t 5 = 1 5 (et - e-4t )
- 18. Segundo teorema de translación • Segundo teorema de traslación para encontrar la transformada de laplace de una función escalón unitario multiplicada por f(t-a). El teorema nos dice que la transforma de laplace del producto de f(t-a) por la función escalón unitario en a es igual a e^-as por la transformada de f(t) Nótese que f(t) resulta de sustituir a t-a por t en f(t-a) Adicionalmente se desprende de esta propiedad que la transformada de la función escalón unitario en a es igual a e^- as / s siendo f(t-a) = 1
- 19. Ejemplo
- 20. Transformada de una función periodica • Teorema que permite encontrar la transformada de laplace de una función periódica. Las funciones con período T tales que f(t) = f(t+T) se pueden transformar al espacio s a través de una fórmula que simplifica su cálculo. Esta fórmula o propiedad se demuestra en este video y se ilustra con ejemplo su forma de uso.
- 21. Desarrollo