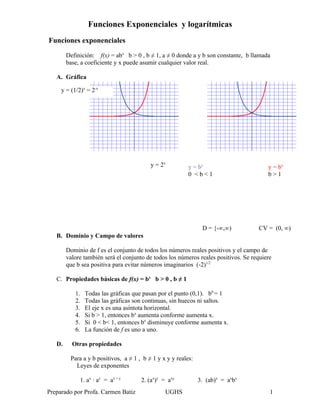
1. Funciones Exponenciales y logarítmicas
Funciones exponenciales
Definición: f(x) = abx b > 0 , b ≠ 1, a ≠ 0 donde a y b son constante, b llamada
base, a coeficiente y x puede asumir cualquier valor real.
A. Gráfica
y = (1/2)x = 2-x
y = 2x y = bx y = bx
0 <b<1 b>1
D = {-∞,∞) CV = (0, ∞)
B. Dominio y Campo de valores
Dominio de f es el conjunto de todos los números reales positivos y el campo de
valore también será el conjunto de todos los números reales positivos. Se requiere
que b sea positiva para evitar números imaginarios (-2)1/2
C. Propiedades básicas de f(x) = bx b > 0 , b ≠ 1
1. Todas las gráficas que pasan por el punto (0,1). b0 = 1
2. Todas las gráficas son continuas, sin huecos ni saltos.
3. El eje x es una asíntota horizontal.
4. Si b > 1, entonces bx aumenta conforme aumenta x.
5. Si 0 < b< 1, entonces bx disminuye conforme aumenta x.
6. La función de f es uno a uno.
D. Otras propiedades
Para a y b positivos, a ≠ 1 , b ≠ 1 y x y y reales:
Leyes de exponentes
1. ax ∙ ay = ax + y 2. (ax)y = axy 3. (ab)x = axbx
Preparado por Profa. Carmen Batiz UGHS 1

2. x
a ax ax
4.   = x 5. x = a x − y
b b a
x y
6. a = a si y sólo si x = y
7. Para x ≠ 0 , entonces ax = bx si y sólo sí a = b
Ejemplo: 4x-3 = 8
(22)x – 3 = 23 se expresa el 4 y el 8 como potencia de 2
22x – 6 = 23 (ax)y = axy
2x – 6 = 3 Propiedad 2
2x = 9
x=4½
E. Aplicación P = población en el tiempo t
P0 = población en el tiempo t = 0
1. Crecimiento demográfico d = tiempo de duplicación
La bacteria Escherichia coli ( E. coli) se Cuando t = d P = P02t/d = P02
encuentra naturalmente en los intestinos de
muchos mamíferos. En un experimento de laboratorio, se encuentra que el
tiempo de duplicación para la E. coli es de 25 minutos. Si el experimento
comienza con una población de 1000 E. coli y no hay ningún cambio en el
tiempo de duplicación, ¿cuántas bacterias estarán presentes:
a. en 10 minutos ? b. en 5 horas? = 300 minutos
P0 = 1,000 minutos d = 25 minutos
a. P = (1,000) (210/25) = 1,320 E. colí
b. P = (1,000) (2300/25) = 4,096,000 = 4.1 x 106 E. colí
1. Decaimiento radiactivo
A = cantidad al tiempo t
198
El oro radiactivo 198( Au) que se usa en A0 = cantidad al tiempo t = 0
las radiografías del hígado tiene una vida h = vida media
media de 2.67 días. Si se empieza con 50
miligramos del isótopo, ¿Cuántos A = A02-t/h
miligramos quedarán después de:
a. ½ día? b. una semana?
A0 = 50 mg h = 2.67 días
a. A = 50(2-.5/2.67) = 50 = 43.9 mg
2.5/2.67
-7/2.67
b. A = 50(2 ) = 50 = 8.12 mg
2 7/2.67
2. Interés compuesto A = cuenta al final del año t años
P = capital
Si se invierten $1,000 en una cuenta que r = interés compuesto
paga el 10% de interés compuesto n = cantidad al año
mensualmente, ¿cuánto habrá en la cuenta
después de 10 años? Redondea a la r
centésima más cercana. A = P (1 + ) nt
n
Preparado por Profa. Carmen Batiz UGHS 2

3. P = $1,000 r = .10 n = 12 t = 10 años
.10 (12)(10)
A = 1,000(1 + ) = $2,707.04
12
Ejercicios 4.1
Preparado por Profa. Carmen Batiz UGHS 3

4. Funciones Exponenciales de base e
A. Definición
f(x) = ex x es un número real
B. Gráfica
y = 4 – ex/2
y = ex y = e-x
y = 4 asíntota horizontal
x → ∞ ex/2 → 0 y 4 y → 4
C. Aplicación N= número de bacterias presentes después
de t horas
1. Medicina -Crecimiento bacteriano N0 = número de bacterias presentes
El cólera es una enfermedad intestinal cuando t = 0
causada por la bacteria del cólera que se t = tiempo de duplicación
multiplica exponencialmente por la
división de células modelada por la N = N0e1.386t
fórmula presentada. Si se empieza con
una bacteria, ¿cuántas bacterias habrá en a. 5 horas? b. 12 horas? Calcule sus
respuestas con tres dígitos significativos.
N0 = 1 t = 5 horas a. N = 1 e(1.386) (5) = e(1..386) (5) = 1,020
t = 12 horas b. N = 1 e(1.386) (12) = e(1.386) (12) = 16,700,000 .
2. Cálculo de fechas conel carbono 14
A = cantidad al carbono 14 presente
El bombardeo de rayos-cósmicos de la en t años
atmósfera produce neutrones, los que al A0 = cantidad al tiempo t = 0
regresar reaccionan con el nitrógeno y t = tiempo
producen carbono 14 radiactivo. El carbono
14 radiactivo penetra en los tejidos de todos A = A0e-0.000124t
los seres vivos a través del dióxido de carbono, el cual es absorbido primero por las plantas.
Mientras que la planta o el animal esté vivo, el nivel de carbono 14 en el organismo se
mantiene constante, Una vez que el organismo muere, el carbono 14 disminuye de acuerdo
con la ecuación. Si 1000 mg de carbono 14 están presentes en un inicio, ¿cuántos miligramos
estarán presentes en:
a. 10,000 años b. 50,000 años?
4

5. A0 = 1,000 mg a. A = 1000e-0.000124(10,000) = 289 mg
b. A =
1000e-0.000124(50,000) = 2.03 mg A = cuenta al final del año t años
3. Interés compuesto continuo P = capital invertido a una tasa anual r
r = tasa anual
Si se invierten $100 a una tasa anual del t = cantidad al año
8% de interés compuesto continuamente,
¿qué cantidad, aproximada al centésimo A = Pe rt
más cercano, estará en la cuenta después
de 2 años?
P = $100 r = .08 t = 2 años
= $117.35
A = 100e (.08)( 2 )
D. Crecimiento y decaimiento exponencial
Crecimiento sin límite y = cekt c, k > 0 Decaimiento exponencial y = ce-kt c, k > 0
y y
c t c c
t c y
c
t
c
Crecimiento de la población a corto plazo Decaimiento radiactivo, absorción de luz
(personas, bacterias, etcétera; crecimiento de en agua, vidrio, etcétera; presión
dinero a un interés compuesto continuo. atmosférica.
M
Crecimiento limitado y = c(1- e-kt ) c, k > 0 Crecimiento logístico y = c, k , M > 0
1 + ce − kt
y y
c M
t c
t c
Habilidades de aprendizaje, últimas Crecimiento de la población a largo plazo;
ventas; crecimiento de la compañía; epidemias, ventas de nuevos productos;
circuitos eléctricos. crecimiento de una compañía.
Ejercicios p. 301-302
Ejercicios p. 292-293
Tomado del libro Pre-Cálculo 5
Funciones y sus Gráficas –
Barnett-Ziegler-Byleen

6. Funciones logarítmicas
A. Definición
forma logarítmica forma exponencial
y = log b x equivalente x = by si b > 0 y b ≠ 1
y = log 10 x x = 10y
y = loge x x = ex
y = 2x y=x
B. Gráfica
x= 2y = f-1
D (f) = (-∞,∞) = CV de f-1
CV de f = (0, ∞) = D de f-1
C. Conversiones logarítmicas a exponenciales
Ejemplos : a. log 2 8 = 3 b. log 25 5 = ½ c. log 2 ¼ = -2
8 = 23 5 = 251/2 ¼ = 2-2
Ejemplos : a. 49 = 72 b. 3 = 9 c. 1/5 = 5-1
log 7 49 = 2 log 9 3 = ½ log 5 (1/5)= -1
D. Resolviendo ecuaciones con logarítmos
Ejemplos: Encuentra y : y = log 9 27
27 = 9y cambiando a forma exponencial
33 =32y escribir cada número con la misma base
3 = 2y propiedad de exponentes
3/2 = y
E. Propiedades de las funciones logarítmicas
Si b, M y N son números reales positivos, b ≠1, y p y x son números reales, entonces:
1. log b 1 = 0 5. log b MN = log b M + log b N
2. log b b = 1 M
6. log b = log b M − log b N
3. log b bx = x N
4. blogb x = x , x > 0 7. log b Mp = p log b M
8. log b M = log b N si y sólo si M = N
6

7. Ejemplos: a. log 10 10-5 = -5 propiedad # 3
b. log 5 25 = log 5 52 = 2 propiedad #3
c. log 10 1 =0 propiedad #1
m+n
d. log e e = m+n propiedad #3
e. 10 log104 = 4 propiedad #4
f. eloge(x4 + 1) = x4 + 1 propiedad #4
r
g. log b = logb r - (logb u + logbv) = logb r - logb u - logbv Prop
uv
5y6
3/ 5
m
h. log b   = (3/5) (logb m - logb n) Prop 6 y 7
n
u1/ 3
i. log b 5 = (1/3) logb u - 5 logb v Prop 6 y 7
v
510
j. log e 5 = 1.609 y log e 8 = 2.079, encuentre log e
8
510
log e = 10 loge 5 - loge 8 = 10(1.609) – 2.079 = 14.01
8
8
k. log e 5 = 1.609 y log e 8 = 2.079, encuentre log e 4
5
8
(si ¼ = .25 ) log e 4 = .25 (loge 8 - loge 5) = .25 (2.079 - 1.609)
5
= 0.1175
l. Encuentre x, tal que log b x = 2/3 log b 8 + ½ log b 9 – log b 6 sin
usar calculadora o tabla.
log b x = 2/3 log b 8 + ½ log b 9 – log b 6
= log b 8 2/3 + log b 91/2 – log b 6
= log b 4 + log b 3 – log b 6
(4 ⋅ 3) 82 / 3 = 3 82 = 3 2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 2 = 4
= log b
6
91/ 2 = 9 = 3
log b x = log b 2
x=2
Errores comunes :
log b M
1. ≠ log b M − log b N
log b N
Ejercicios p. 312-313
2. log b ( M + N ) ≠ log b M + log b N
7

8. Logaritmos communes y naturales
A. Definición
log x = log10 x logaritmo común
ln x = loge x logaritmo natural
B. Uso de la calculadora para hallar logaritmos
Ejemplos: Utiliza la calculadora para evaluar cada una con seis cifras decimales.
a. log 3184
Utilizando la techa 10x entra 3184 = 3.502973
b. ln 0.000349
Utilizando la techa ex entra 0.000349 = -7.960439
c. log(-3.24) = error
ln 3
d. = 14.27549
ln 1.08
3
e. ln = 1.02165
1.08
f. ln 3 – ln 1.08 = 1.02165
C. Relaciones logarítmicas y exponenciales
Log x = y es equivalente a x = 10x
Ln x = y es equivalente a x = ex
Ejemplos: Encuentre x con tres dígitos significativos, dados los logaritmos indicados.
a. log x = -9.315
x = 10-9.315
x = 4.84 x 10-10
b. ln x = 2.386
x = e2.386
x = 10.9
8

9. D = nivel de decibeles del sonido
I = intensidad del sonido
Io = 10-12 w/m2 (estandarizado)
D. Aplicaciones
D = 10 log I
1. Intensidad del sonido I0
Encuentra el número de decibeles de un cuchicheo con intensidad de sonido de
5.20 x 10-10 watt por metro cuadrado. Calcule la respuesta hasta dos cifras
decimales.
D = 10 log I D = 10 log 5.20 x 10-10
I0 10-12
= 10 log (5.20 x 102)
= 10 (log 5.20 + log 102)
= 10 (0.716 +2)
= 27.16 decibeles
2. Intensidad de un terremoto
M = magnitud en la escala Richter
El terremoto de 1985 en Chile liberó E = energía liberada por el terremoto
aproximadamente 1.26 x 1016 joules de Eo = 104.40 joules (estandarizado)
energía. ¿cuál fue su magnitud en la escala de
Richter? Calcule la respuesta con dos cifras 2 E
M = log
decimales? 3 E0
2 E 2 1.26 x1016
M = log M = log
3 E0 3 10 4.40
2
M = log1.26 x1011.60
3
2
M = (log1.26 + log 10 )
11.60
3
2
M = (0.100 + 11.60) = 7.80
3
3. Teoría de vuelo de un cohete
v = velocidad de un cohete al apagarse cuando
se agota el combustible
En una etapa típica, el combustible sólido de un c = velocidad de escape de motor del cohete
cohete puede tener una razón de peso W1/Wb = W1 = peso de partida (combustible, estructura y
18.7 y una velocidad de escape c = 2.38 km/s. carga útil)
¿Alcanzaría este cohete una velocidad de Wb = peso consumido (estructura y carga útil)
lanzamiento de 9.0 km/s
W1
v = c ln
W1 Wb
v = c ln v = 2.38 ln 18.7
Wb
v = 6.97 km/s
No alcanzará llegar a la órbita por ser menor a 9.0 km/s
Ejercicios de Práctica
Tomado del libro: Pre- Cálculo Ejercicios p. 321- 322
Funciones y Gráficas
Barnett – Ziegler-Byleen 9

10. Funciones Exponenciales y Logarítmicas
Libro: Pre-Cálculo Funciones y sus Gráficas
Barnett, Ziegler y Byleen
10

11. 11