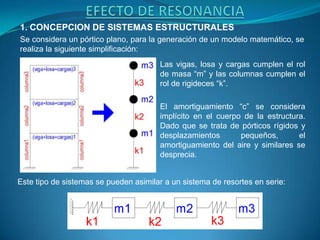
1. EFECTO DE RESONANCIA 1. CONCEPCION DE SISTEMAS ESTRUCTURALES Se considera un pórtico plano, para la generación de un modelo matemático, se realiza la siguiente simplificación: Las vigas, losa y cargas cumplen el rol de masa “m” y las columnas cumplen el rol de rigideces “k”. El amortiguamiento “c” se considera implícito en el cuerpo de la estructura. Dado que se trata de pórticos rígidos y desplazamientos pequeños, el amortiguamiento del aire y similares se desprecia. Este tipo de sistemas se pueden asimilar a un sistema de resortes en serie:

2. EFECTO DE RESONANCIA A partir del cuerpo libre del caso mas simple (sistema de 1 grado de libertad) se deduce la ecuación diferencial que gobierna el régimen de movimiento. Fi + Fd + Fs = P(t) Fi es la fuerza de inercia, Fd es la fuerza de amortiguamiento, Fs es la fuerza de rigidez y P es una carga variable en e tiempo. Se escribe la ecuación en términos diferenciales: Donde U es el desplazamiento. La resolución de la ecuación diferencial da como resultado una expresión matemática de U en función del tiempo U(t)

5. EFECTO DE RESONANCIA De acuerdo al cuerpo libre del sistema, la ecuación base para carga armónica es: En la realidad es muy difícil estimar valores de amortiguamiento. Uno de los capítulos próximos trata exclusivamente ese tema. Por ahora se empelara el mas sencillo de todos que es el amortiguamiento viscoso, su introducción modifica la ecuación base de la siguiente manera: Reaparece un termino conocido que es la frecuencia natural de la estructura w = frecuencia natural de la estructura Tal como la frecuencia de carga, este valor representa la inversa del periodo, pero no de variación de la carga sino el periodo natural del sistema. Ocurre que una estructura, de acuerdo a su configuración geométrica, asignación de secciones, distribución de masas, rigideces y sistema de amortiguamiento, tiene al menos una forma característica de oscilar y esta es armónica, es decir, cumple un patrón sinusoidal matemáticamente determinable

6. EFECTO DE RESONANCIA Por lo anterior, la estructura oscilara según su modo natural de vibrado y cumplirá un ciclo cada periodo T, por lo mismo tendrá una frecuencia natural w. En la figura se ve el modo de vibrado natural. Debe recalcarse que no se trata de una deformación ocasionada por un estimulo externo (carga), sino un modo natural que tiene la estructura para oscilar y que es ante todo un parámetro fisicomatemático teórico.

7. EFECTO DE RESONANCIA La solución de la ecuación base se disgrega en una Sol. Particular y una complementaria (siguiendo las reglas de la matemática diferencial) que sumadas dan la solución total: Donde C1 y C2 dependen de las condiciones de frontera. Graficando la respuesta en función del tiempo se tendrá: Dentro de esta ecuación aparece la relación entre la frecuencia de la carga y la frecuencia natural de la estructura, fundamental para el análisis de resonancia, que se denotara:

8. EFECTO DE RESONANCIA 3. CONCEPTO MODOS DE VIBRADO Se parte del problema de autovalor-autovector, que es un problema vectorial que se expande para obtener polinomios de grado “n”, donde “n” es el numero de nudos de la estructura. Para hallar cada autovalor debe resolverse un sistema de homogéneo basado en el llamado autovector (que se determina en función de las propiedades de cada nudo). Como una estructura tiene gran cantidad de nudos, el problema se trata matricialmente, donde la masa “m” es reemplazado por la matriz de masas [M], la rigidez “k” es reemplazada por la matriz de rigidez [K]: Donde l son los autovalores y {q} son los autovectores. El problema tiene solución no trivial si y solo si: El análisis matemático es demasiado largo para desarrollar en una presentación, pero halla en el texto base de la asignatura.

9. EFECTO DE RESONANCIA Sin embargo, la interpretación física será: una estructura, de acuerdo a su configuración geométrica, asignación de secciones, distribución de masas, rigideces y sistema de amortiguamiento, tiene al menos una forma característica de oscilar y esta es armónica, es decir, cumple un patrón sinusoidal matemáticamente determinable. Como puede observarse, el pórtico se ha simplificado según lo explicado anteriormente y se obtiene una estructura con UN nudo. En azul puede verse su posibilidad física de oscilación y un análisis intuitivo del problema (que se ratifica con el empleo de las herramientas matemáticas mostradas en la anterior diapositiva), permite inferir que esta es la UNICA posibilidad física de oscilación y por tanto el UNICO modo de vibrado.

10. EFECTO DE RESONANCIA Se presenta otra estructura, esta vez con dos nudos: Puede verse en azul una posibilidad de oscilación y en rojo otra y resulta evidente que físicamente no existe ninguna posibilidad mas de oscilación. Se entiende entonces que una estructura de “n” nudos tiene “n” autovalores-autovectores y cada uno de ellos representa un modo de vibrado. Por lo tanto, una estructura tiene tantos modos de vibrados como nudos contenga.

11. EFECTO DE RESONANCIA Otro aspecto que resulta destacable es que el tiempo en que el primero modo de vibrado (en azul) cumpla un ciclo será distinto del tiempo que le tome al segundo (en rojo). Este hecho también es verificable matemáticamente y a partir de ello podemos afirmar que a cada modo de vibrado le esta asociado intrínsecamente un valor determinado y distinto de periodo y su correspondiente “frecuencia natural”. De ello se deduce que una estructura de “n” tendrá “n” modos de vibrado con “n” frecuencias naturales asociadas a los mismos. Esta idea también es importante al momento de analizar resonancia.

12. EFECTO DE RESONANCIA 4. DEFORMACIONES Nuevamente reiteramos que los modos de vibrado NO son deformaciones reales, sino “posibilidades” de oscilación inherentes al sistema. Nótese que existe una diferencia conceptual primordial: los desplazamientos son una función U(t) dependiente del tiempo y aunque hay infinidad de valores de U para infinidad de valores de t la solución es “única” y es la función U(t), es decir, se tiene una respuesta continua, mientras que los modos de vibrado no dependen del tiempo y de modo fijo existirán tantos como tenga la estructura, entonces siempre su numero será finito y su forma invariante en el tiempo, es decir, se trata de un parámetro discreto. De hecho, en consecuencia con lo anterior, los desplazamientos U(t) están en función de los modos de vibrado. Si a la ecuación base se le introduce el concepto de autovalor-autovector, esta se vectorializa y queda: Cuya solución se obtendrá resolviendo la ecuación diferencial vector-matricial:

13. EFECTO DE RESONANCIA La resolución matemática de la anterior expresión es larga y compleja (esta dada en el texto base), pero su consecuencia física es que la función deformación U(t) es una combinación lineal de todos los modos de vibrado: Donde aii son constantes dependientes de las condiciones de frontera del problema y en los hechos representan porcentajes de participación de cada modo de vibrado li. Como consecuencia de lo anterior, la suma de todos estos coeficientes debería ser igual a 1. La variabilidad de estos porcentajes suele aproximarse a una curva exponencial, entonces, no es necesario considerar todos los modos de vibrado. Para una estructura sostenida por pórticos (un edificio que puede tener miles de nudos), suelen ser suficientes los primeros 12 a 15 modos de vibrado, que están asociados a sus propias frecuencias naturales de vibración y también a determinados porcentajes de masa. Se considera que sumados los porcentajes de masa de los modos de vibrado considerados representen el 90% de la masa total del edificio. A continuación se proporciona una tabla guia:

14. EFECTO DE RESONANCIA 4. RESONANCIA El concepto físico de resonancia es bastante simple. Se presenta cuando la frecuencia de la carga es igual a la frecuencia natural del sistema, es decir: El efecto físico de esta situación es que se magnifica la respuesta, es decir, las deformaciones, tal como se observo en el video. La representación matemática de lo anterior se realizara para el caso mas simple (un grado de libertad) y es como sigue: se tiene la solución: Se considera únicamente la respuesta estable y se extrae el siguiente factor:

15. EFECTO DE RESONANCIA Sabiendo que Po/K es la respuesta estática, es decir, sin cargas dinámicas, se tendrá el factor de magnificación dinámica: Graficando esta expresión se tiene: Como puede verse, el factor de magnificación D, y por ende las deformaciones, crece mas mientras mas el valor de b se acerca a 1, es decir, mientras la frecuencia de carga W se acerca mas al valor de la frecuencia natural del sistema w.

16. EFECTO DE RESONANCIA Sin embargo, como se vio anteriormente, no existe una sola frecuencia natural de vibrado, sino tantas como modos de vibrado existan y aunque se recomendó que no se empleen todos los modos de vibrado, no queda claro que modo de vibrado y que frecuencia natural asociada debe usarse. Como se vio en la tabla adjunta, los primeros modos de vibrado son los que mayor porcentaje de masa asociada tienen, normalmente son los 3 o 4 primeros, entonces, inicialmente bastara considerar solo las frecuencias naturales asociadas a estos 3 o 4 MDV. Pero aun se pueden hacer mayores simplificaciones teóricas. El problema consiste en evitar que , entonces, como la frecuencia de la carga W es un dato invariante (condición del problema), solo se puede modificar la frecuencia natural del sistema w haciéndola mas grande o mas pequeña, sin embargo, normalmente las frecuencias de carga W suelen ser bastante altas, entonces conviene hacer la frecuencia natural w lo mas baja posible y es el primer modo de vibrado el que ofrece los valores mas bajos además de tener asociada la mayor cantidad de masa, por tanto, se trabajara únicamente con este modo de vibrado y su frecuencia natural w asociada

19. EFECTO DE RESONANCIA 4. MODELOS MATEMATICOS Todo el desarrollo matemático involucrado se circunscribe en la creación de modelos matemáticos, hasta ahora simplificados. A continuación se realizara la resolución fisicomatemática del siguiente problema:

20. EFECTO DE RESONANCIA 4. MODELOS MATEMATICOS Se vera que se parte de la simplificación siguiente: Para la resolución, la ecuación base debe matricializarse de la siguiente manera: con: El resultado será la obtención de las deformaciones U(t) pero para los 4 nudos del modelo (derecha) y no para los 7 nudos reales y tendrá que realizarse una desagregación matemática adicional. Sin embargo, existen problemas mucho mas complejos como la resolución de pórticos en 3 dimensiones

21. EFECTO DE RESONANCIA Se tiene un edificio real en 3 dimensiones. En este caso realizar desagregaciones de U(t) resulta complicado y MUY moroso, por lo que seria preferible un análisis del modelo SIN simplificaciones.

22. EFECTO DE RESONANCIA Ello implicaría, por ejemplo, para la matriz de rigidez [k] hacer consideraciones físicas basadas en la ley de Hooke, que como consecuencia arrojarían una matricializacion mas complicada:

23. EFECTO DE RESONANCIA Lo anterior debe hacerse para cada barra del edificio, ya que las cuatro matrices de rigidez mostradas anteriormente, que almacenan parámetros se área, material, geometría e inercia, inevitablemente consideran los dos nudos de una sola barra y su cuerpo mismo en coordenadas locales. El mismo tratamiento tendría que hacerse con las masas y los amortiguamientos; a ello súmele la forma vectorializada de la ecuación base (autovalor-autovector) y si además, existen barras (vigas o columnas) de sección variable, el símbolo de diferencial debería entrar dentro de cada matriz para resolver estos gradientes continuos de sección. Como se ve, el modelo matemático se complica tanto que su resolución resulta inviable en términos prácticos. Por ello antiguamente no se realizaban cálculos dinámicos, sino simplemente estáticos y se afectaban por factores de seguridad. El adelanto tecnológico ha permitido la invención de software especializado que permite resolver modelos matemáticos tan complejos como el descrito, de modo que los antiguos métodos han sido reemplazados por la modelación digital mediante de software especializado. Sin embargo, el empleo de estas aplicaciones es inútil e incluso PELIGROSO sin una solida base teórica fisicomatemática. La siguiente clase estará exclusivamente dedicada al manejo del paquete SAP2000 V.14.0.0. que es el software especializado tecnológicamente mas confiable para estos tipos de análisis y la creación de modelos digitales.