Matemática Superior, Límites.

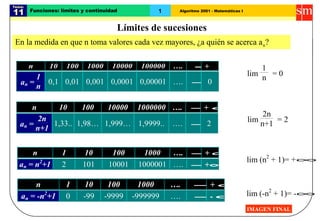
1. Algoritmo 2001 - Matemáticas I
Tema:
11 1Funciones: límites y continuidad
En la medida en que n toma valores cada vez mayores, ¿a quién se acerca an?
n 10 100 1000 10000 100000 …. →+∞lim
1
n
= 0
n 10 100 10000 1000000 …. →+∞
lim
2n
n+1
= 2
n 1 10 100 1000 …. →+∞
lim (n2
+ 1)= +∞
n 1 10 100 1000 …. →+∞
lim (-n2
+ 1)= -∞
Límites de sucesiones
an =
1
n
0,1 0,01 0,001 0,0001 0,00001 …. →0
an =
2n
n+1
1,33.. 1,98… 1,999… 1,9999.. …. →2
an = n2
+1 2 101 10001 1000001 …. →+∞
an = -n2
+1 0 -99 -9999 -999999 …. →- ∞
IMAGEN FINAL

2. Algoritmo 2001 - Matemáticas I
Tema:
11 2
0
0,1
0,2
0,3
0,4
0,5
0,6
0,7
0,8
0,9
1
0 5 10 15 20 25 30 35 40 45 50 55 60 65 70 75 80 85 90 95 100
a20
Funciones: límites y continuidad
Representación de los términos de la sucesión an = 1/n
a1
a2
a3
a50 a96
IMAGEN FINAL

3. Algoritmo 2001 - Matemáticas I
Tema:
11 3
1
1,1
1,2
1,3
1,4
1,5
1,6
1,7
1,8
1,9
2
2,1
0 5 10 15 20 25 30 35 40 45 50 55 60 65 70 75 80 85 90 95 100
a20
Funciones: límites y continuidad
Representación de los términos de la sucesión an = 2n/(n + 1)
a1
a2
a3
a50
a96
IMAGEN FINAL

4. Algoritmo 2001 - Matemáticas I
Tema:
11 4
0
500
1000
1500
2000
2500
3000
3500
4000
4500
5000
5500
6000
6500
7000
7500
8000
8500
9000
9500
10000
0 5 10 15 20 25 30 35 40 45 50 55 60 65 70 75 80 85 90 95 100
Funciones: límites y continuidad
Representación de los términos de la sucesión an = n2
+ 1
a20
a50 a90
a5
IMAGEN FINAL

5. Algoritmo 2001 - Matemáticas I
Tema:
11 5
-10001
-9501
-9001
-8501
-8001
-7501
-7001
-6501
-6001
-5501
-5001
-4501
-4001
-3501
-3001
-2501
-2001
-1501
-1001
-501
-1
0 5 10 15 20 25 30 35 40 45 50 55 60 65 70 75 80 85 90 95 100
Funciones: límites y continuidad
Representación de los términos de la sucesión an = -n2
+ 1
a20
a50
a90
a5
IMAGEN FINAL

6. Algoritmo 2001 - Matemáticas I
Tema:
11 6
-2500
-2000
-1500
-1000
-500
0
500
1000
1500
2000
2500
0 5 10 15 20 25 30 35 40 45 50
a10
Funciones: límites y continuidad
Representación de los términos de la sucesión an = (-1)n .
n2
a1
a44
a23
Esta sucesión no tiene límite
IMAGEN FINAL

7. Algoritmo 2001 - Matemáticas I
Tema:
11 7Funciones: límites y continuidad
n 10 100 1000 10000 100000 …. →+∞
lim








1 +
1
n
n
= e
El número e






1 +
1
n
n
2,59374246012,704813829422 2,716923932236 2,718145926825 2,718268237192 …. →e
IMAGEN FINAL

8. Algoritmo 2001 - Matemáticas I
Tema:
11 8
2
2,1
2,2
2,3
2,4
2,5
2,6
2,7
2,8
0 5 10 15 20 25 30 35 40 45 50 55 60 65 70 75 80 85 90 95 100
a20
Funciones: límites y continuidad
Representación de los términos de la sucesión an = (1+1/n)n
a1
a2
a3
a50
a96
IMAGEN FINAL

9. Algoritmo 2001 - Matemáticas I
Tema:
11 9Funciones: límites y continuidad
En la medida en que x toma valores cada vez más próximos a “a”,
¿a quién se acerca f(x)?
x 1 1,9 1,99 1,999 …. →2-
x→2-
lim x2
= 4
x 3 2,1 2,01 2,001 …. →2+
x→2+
lim x2
= 4
x 1 1,9 1,99 1,999 …. →2-
x→2-
lim Ent(x) = 1
x 3 2,1 2,01 2,001 …. →2+
x→2+
lim Ent(x) = 1
Límites de funciones en un punto
f(x) = x2
1 3,6 3,96 3,996 …. →4
f(x) = x2
9 4,4 4,04 4,004 …. →4
f(x) = Ent(x) 1 1 1 1 …. →1
f(x) = Ent(x) 3 2 2 2 …. →2
IMAGEN FINAL

10. Algoritmo 2001 - Matemáticas I
Tema:
11 10Funciones: límites y continuidad
En la medida en que x se hace muy grande, con valores positivos ¿a quién se acerca f(x)?
x 1 10 100 1000 …. →+∞
x→+∞
lim x2
= +∞
x→-∞
lim x2
= +∞
x 1 10 100 1000 …. →+∞
x→+∞
lim
x + 1
x
= 1
En la medida en que x se hace muy grande, con valores negativos ¿a quién se acerca f(x)?
x -1 -10 -100 -1000 …. →-∞
x -1 -10 -100 -1000 …. →-∞
x→- ∞
lim
x + 1
x
= 1
Límites de funciones en el infinito
f(x) = x2
1 100 10000 1000000 …. →+∞
f(x) =
x + 1
x
2 1,1 1,01 1,001 …. →1
f(x) = x2
1 100 10000 1000000 …. →+∞
f(x) =
x + 1
x
0 0,9 0,99 0,999 …. →1
IMAGEN FINAL

11. Algoritmo 2001 - Matemáticas I
Tema:
11 11
- 4 - 2 2 4 6 8 10
2
4
6
8
10
y =
x + 1
x - 1
Funciones: límites y continuidad
x→+∞
lim
x + 1
x - 1
= 1
Significado geométrico del límite finito de una función, para x → + ∞
IMAGEN FINAL

12. Algoritmo 2001 - Matemáticas I
Tema:
11 12
- 4 - 2 2 4 6 8 10
2
4
6
8
10
y =
x + 1
x - 1
Funciones: límites y continuidad
x→1+
lim
x + 1
x - 1
= +∞
Significado geométrico del límite infinito de una función para x
tendiendo a un número real
IMAGEN FINAL

13. Algoritmo 2001 - Matemáticas I
Tema:
11 13Funciones: límites y continuidad
•
x→3
lim
x + 1
x - 1
=
•
x→1
lim
x + 1
x - 1
=
x→1+
lim
x + 1
x - 1
= + ∞
x→1−
lim
x + 1
x - 1
= - ∞
•
x→+∞
lim
x + 1
x - 1
=
x→+∞
lim
1 +
1
x
1 -
1
x
= 1
Indet
k
0
Indet
∞
∞
No hay indeterminación
4
2
= 2
Cálculo de límites (I)
IMAGEN FINAL

14. Algoritmo 2001 - Matemáticas I
Tema:
11 14Funciones: límites y continuidad
•
x→1
lim
x2
- 1
x - 1
=
•
x→−∞
lim
x + 1
x - 1
=
x→−∞
lim
1 +
1
x
1 -
1
x
= 1
Indet
0
0
Indet
∞
∞
x→1
lim
(x - 1)(x + 1)
x - 1
= 2
Cálculo de límites (II)
IMAGEN FINAL

15. Algoritmo 2001 - Matemáticas I
Tema:
11 15Funciones: límites y continuidad
•
x→0
lim
x
1 - 1 - x
= 2
Indet
0
0
x→0
lim
x(1 + 1 - x)
(1 - 1 - x) (1 + 1 - x)
=
x→0
lim ( 1 + 1 - x) =
•
x→+∞
lim
x2
+ x
x
=
Indet
∞
∞
x→+∞
lim
1 +
1
x
1
= 1
•
x→−∞
lim
x2
+ x
x
=
Indet
∞
∞
x→+∞
lim
1 -
1
x
-1 = -1
x→+∞
lim
x2
- x
-x =
Cálculo de límites (III)
IMAGEN FINAL

16. Algoritmo 2001 - Matemáticas I
Tema:
11 16Funciones: límites y continuidad
Estudio del
x→0
lim
sen x
x
. Se pone la calculadora en modo Rad para construir las siguientes tablas.
x 0,1 0,01 0,001 0,0001 0,00001 0,0000001
sen x
x
0,998334166468 0,999983333416 0,999999833333 0,999999998333 0,99999999998 0,999999999999
x - 0’1 - 0’01 - 0’001 - 0’0001 - 0’00001 - 0’0000001
sen x
x
0,998334166468 0,999983333416 0,999999833333 0,999999998333 0,99999999998 0,999999999999
Los resultados sugieren que
x→0+
lim
sen x
x
=1
Los resultados sugieren que
x→0-
lim
sen x
x
=1
En consecuencia:
x→0
lim
sen x
x
=1
Límites de funciones trigonométricas
IMAGEN FINAL

17. Algoritmo 2001 - Matemáticas I
Tema:
11 17Funciones: límites y continuidad
El
x→0
lim
sen x
x geométricamente
 10  5 5 10
 0.2
0.2
0.4
0.6
0.8
1
• La función no está
definida en 0.
• Pero está definida en
las proximidades del
punto 0
IMAGEN FINAL

18. Algoritmo 2001 - Matemáticas I
Tema:
11 18Funciones: límites y continuidad
Gráfica de la función f (x) =


x+1 si x ≤0
x - 1 si x > 0
x + 1 si x ≤ 0 x - 1 si x >0
X
Y
1
-1
-1
1
•
x→0+
lim f(x) =
x→0+
lim (x - 1) = -1
•
x→0-
lim f(x) =
x→0-
lim (x + 1) = 1
•f(0) = 1
f(x) no es continua en el punto xo = 0
Continuidad en un punto
IMAGEN FINAL