Aplikasi integral
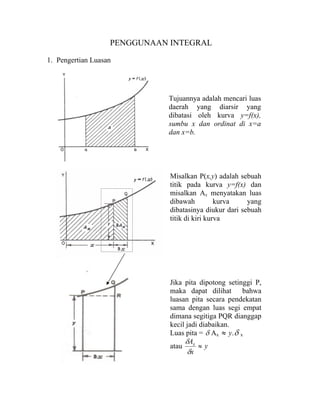
- 1. PENGGUNAAN INTEGRAL 1. Pengertian Luasan Tujuannya adalah mencari luas daerah yang diarsir yang dibatasi oleh kurva y=f(x), sumbu x dan ordinat di x=a dan x=b. Misalkan P(x,y) adalah sebuah titik pada kurva y=f(x) dan misalkan Ax menyatakan luas dibawah kurva yang dibatasinya diukur dari sebuah titik di kiri kurva Jika pita dipotong setinggi P, maka dapat dilihat bahwa luasan pita secara pendekatan sama dengan luas segi empat dimana segitiga PQR dianggap kecil jadi diabaikan. Luas pita = δ Ax ≈ y.δ x atau y x Ax ≈ δ δ
- 2. (a) (b) Jika ruas kanan dan kiri diintegrasi maka didapat sbb : Jika Ax = ∫ dxy menyatakan luas daerah sampai ke titik P(x,y). ` Jika proses diteruskan bidang gb. a dipenggal sebanyaknya menjadi gb. b sehingga 0→xδ akhirnya kesalahan daerah yang diarsir ini hilang maka dx dA x A xx → δ δ y dx dAx =∴ (bukan pende- katan lagi) dapat diabaikan a) Jika subsitusikan x=b, diperoleh luas daerah sampai ke titik L yaitu Ab = ∫ dxy dgn x=b. b) Jika subsitusikan x=a, diperoleh luas daerah sampai ke titik K yaitu Aa = ∫ dxy dgn x=a. cxF dxxfdxyAx += == ∫∫ )( )(
- 3. Jika hasil pertama kurangi dengan hasil kedua, akan diperoleh luas kurva diantara ordinat x = a dan x=b. a dan b adalah harga batas integral. 2. Luas Bidang Datar a. Luas di atas sumbu x misalkan )(xfy = adalah grafik diatas sumbu x dan f kontinu dan tidak negatif pada selang bxa ≤≤ , maka ∫= b a dxxfRA )()( Dimana daerah R dibatasi grafik 0,,),( ==== YbXaXxfy b. Luas di bawah sumbu x misalkan )(xfy = adalah grafik diatas sumbu x dan ∫ b a dxxf )( = bil negatif maka, ∫−= b a dxxfRA )()( yaitu : A=∫ ∫ == − )()( axbx dxydxy bentuk ini ditulis sbb : ∫= b a dxyA a b y x y=f(x) a b y x y=f(x)
- 4. Contoh : Tentukan luas daerah R dibawah kurva 22 34 +−= xxy antara x = -1 dan x = 2 Jawab : luassatuan x xx dxxxRA 7,14 2 2 1 5 1 4 2 16 2 32 2 25 )22()( 2 1 45 2 1 34 = ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ −−−−⎟ ⎠ ⎞ ⎜ ⎝ ⎛ +−= ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ +−= +−= − −∫ 3. Daerah Antara Dua Kurva Kurva-kurva )(xfy = dan )(xfg = dengan )()( xfxg ≤ pada selang bxa ≤≤ Contoh Soal ke-1 Tentukan luas daerah antara kurva 4 1 xy = dan 2 2 2 xxy −= dan sketsa gambar tersebut serta harga batasnya pada sumbu x. a. menentukan harga batas. ⇔ y1 = y2 ⇔ 022 2424 =+−⇒−= xxxxxx ⇔ 0)2)(1)(( 2 =++− xxxx ⇔ 1,0 == xx , x yang lain imaginer (tidak dipakai) [ ] [ ]dxxgxfA xxgxfA b a∫ −= ∆−=∆ )()( )()(
- 5. b. Menentukan bentuk kurva maka nilai x disubsitusi kepersamaan y1 dan dan y2 x y1 y1 0 0 0 0.25 0.0039 0.4375 0.50 0.0625 0.7500 0.75 0.3164 0.9375 0.90 0.6561 0.9900 1 1 1 Dari tabel di atas bila range dirapatkan dan dihubungkan titiknya akan didapat gambar sbb : c. Luas daerah yang dicari adalah pengurangan dari kurva atas dikurangi kurva bawah. ( ) ( )dxxxxA 41 0 2 2∫ −−=⇔ dxxxxA 421 0 2 −−=⇔ ∫ 2 1 0 53 2 15 7 5 1 3 1 1 53 satuan xx xA =−−= ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ −−=⇔
- 6. Contoh Soal ke-2 Tentukan luas daerah yang dibatasi oleh parabola xy 42 = dan garis 434 =− yx , sketsa serta harga batasnya pada sumbu y. a. menentukan harga batas. Pers. 1) xy 42 = atau 4 2 y x = , Pers. 2) 434 += yx atau 4 43 + = y x Pers.1 = Pers.2 Maka : 432 += yy ⇔ 0432 =−− yy 0)1()4( =−−⇔ yy 1,4 −=⇔ y b. Menentukan bentuk kurva maka nilai x disubsitusi kepersamaan y1 dan dan y2 y 4 2 y x = 4 43 + = y x 4 4 4 3 2.25 3.25 2 1 2.50 1 0.25 1.75 0 0 1 -1 0.25 0.25
- 7. Dari tabel di atas bila range dirapatkan dan dihubungkan titiknya akan didapat gambar sbb : c. Luas daerah yang dicari adalah pengurangan dari kurva atas dikurangi kurva bawah. dy yy A ∫− ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ − + =⇔ 4 1 2 44 43 ( )dyyyA ∫− −+=⇔ 4 1 2 43 4 1 4 1 32 3 4 2 3 4 1 − ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ −+= y y y ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ +−−⎟ ⎠ ⎞ ⎜ ⎝ ⎛ −+= 3 1 4 2 3 3 64 1624 4 1 = 21.5 24 125 ≈ satuan2
- 8. Persamaan Parametrik. Persamaan selalu dengan cara yang sama dimana adalah lebih dari dua variabel. Caranya selalu sama yaitu : 1) Nyatakan x dan y dalam parameter. 2) Ubah variabelnya. 3) Sisipkan batas-batas parameternya. Contoh: Suatu kurva memiliki persamaan pametrik atyatx 2,2 == . Tentukan luas luas daerah yang dibatasi oleh kurva tesebut, sumbu x, dan ordinat pada t=1 dan t=2. Jawab : ∫= b a dxyA , a dan b adalah batas variabelnya. Dengan menggantikan y dengan 2 at , didapatkan ∫= b a dxatA 2 Tidak dapat diintegrasi langsung fungsi t terhadap x, maka harus dirubah variabel integrasinya sbb: 2 atx = dtatdxat dt dx 22 =∴=∴ didapatkan : ∫ ∫== 2 1 2 1 22 42.2 dttadtatatA = 2 1 3 2 3 4 ⎥ ⎦ ⎤ ⎢ ⎣ ⎡t a = 3 28 3 1 3 8 4 2 2 a a =⎥⎦ ⎤ ⎢⎣ ⎡ − 3. Harga mean (harga rata-rata) Harga mean adalah rata-rata (average) harga (tinggi) yang ditinjau. Dalam mencari harga mean suatu fungsi )(xfy = diantara x=a dan x=b yang dapat dilihat pada gambar di bawah. Jika memperkirakan tinggi dari gambar dalam diagram maka didapat suatu harga M.
- 9. dan diberikan sbb : M ab A Alas Luas − == ∴ M ∫− = b a dxy ab 1 4. Harga RMS. RMS = Root Mean Square kadang-kadang harga akar dari harga rata- rata. rms = √(harga mean dari y2 atau (rms)2 ∫− = b a dxy ab 21 Contoh : Hitung harga mean dan rms dari fungsi 32 += xy di antara x=1 dan x=3. a) Mean. M ∫ + − = 3 1 2 )3( 13 1 dxx 2 3 1 3 3 2 14 3 3 1 9 3 27 2 1 3 32 1 satuan x x = ⎭ ⎬ ⎫ ⎩ ⎨ ⎧ ⎥⎦ ⎤ ⎢⎣ ⎡ +−⎥⎦ ⎤ ⎢⎣ ⎡ += ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ +=
- 10. b) RMS. (rms)2 ∫− = 3 1 2 13 1 dxy ( )∫ ++= 3 1 24 96 2 1 dxxx 3 1 3 5 92 52 1 ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ ++= xx x ⎭ ⎬ ⎫ ⎩ ⎨ ⎧ ⎥⎦ ⎤ ⎢⎣ ⎡ ++ ⎭ ⎬ ⎫ ⎩ ⎨ ⎧ −⎥⎦ ⎤ ⎢⎣ ⎡ ++= 92 5 1 2754 5 243 2 1 x [ ] 2,592.11816.48 2 1 =−+= rms 694.72.59 == satuan2 5. Volume Benda Putar Benda Putar, dibentuk dengan memutar suatu bidang datar disekeliling sebuah garis, disebut sumbu putar pada bidang datar dapat diketahui melalu cara berikut : a. Metode Cakram. Dibentuk dengan memutar suatu bidang datar sekeliling sebuah garis, disebut sumbu putar pada bidang datar.
- 11. Jika bentuk bidang dibatasi oleh kurva y=f(x), sumbu x , dan ordinat pada x=a dan x=b diputarkan sutu putaran penuh mengelilingi sumbu x, maka akan diperoleh sebuah benda putaran yang simetris terhadap OX seperti gambar di atas. Untuk mendapatkan V, pertama-tama tinjau dahulu sebuah pita sempit dalam bentuk bidang semula. Volume yang dibentuk pita tsb ≈ volume yang dibentuk oleh pita persegi panjang yaitu xyV δπδ .. 2 ≈ berupa selinder pipih. Jika seluruh bentuk selinder dibagi-bagi menjadi sejumlah pita, maka setiap pita akan menghasilkan selindernya sendiri, masing-masing dengan volume xy δπ .. 2 lihat gambar berikut : ∴ Volume total , ∑ = = ≈ bx ax xyV δπ .. 2
- 12. Bila 0→xδ maka kesalahan yang ditimbulkan oleh bagian atas luas persegi panjang dapat dihilangkan menjadi : ∫= b a dxyV .. 2 π Contoh soal : Tentukan volume benda putar yang dibentuk oleh daerah R yang dibatasi oleh kurva xy =2 , sumbu x dan garis x = 4, dimima R diputar mengelilingi sumbu x. Penyelesaian : ∫= b a dxyV .. 2 π , dimana xy = Maka : ( )∫= 4 0 2 .. dxxV π = 4 0 2 4 0 2 ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ =∫ x dxx ππ = 2 16 π = 13.258 ≈π satuan3
- 13. b. Metode Cincin Contoh 1 : Tentukan volume benda putar apabila daerah yang dibatasi oleh parabola- parabola 2 xy = dan xy 82 = diputar mengelilingi sum-bu-x. Sketsa gambar tersebut serta harga batasnya. a. menentukan harga batas. ⇔ y1 = y2 ⇔ xx 82 = ⇔ 084 =− xx ⇔ 0)8( 3 =−xx ⇔ ,0=x dan 2)8( 3 =⇒= xx b. Menentukan bentuk kurva maka nilai x disubsitusi kepersamaan y1 dan dan y2 y 2 xy = xy 8= 2 4 4 1.5 2.25 3.464 1 1 2.828 0.5 0.25 2 0 0 0 Sebuah benda putar dipotong- potong tegak lurus pada sum-bu putarnya, maka diperoleh sebuah cakram yang ditengah-tengah ada lubangnya. Daerah ini disebut Cincin.
- 14. Dari tabel di atas bila range dirapatkan dan dihubungkan titiknya akan didapat gambar sbb : Contoh 2 : Hitung Volume benda putar daerah setengah lingkaran yang dibatasi oleh kurva 2 4 yx −= dan sumbu y diputar mengelilingi garis x = -1 Penyelesaian : Jari-jari luar cincin adalah 14 2 +− y , sedangkan jari-jari dalam adalah 1. hasilnya bila disketsa melalui pentabelan adalah sbb: ( ) ( )[ ] ( ) ( ) 3 2 0 52 2 0 4 222 6.94.616 5 1 4 8 8 satuan xx dxxxV xxxV ππ π π π =−= ⎥⎦ ⎤ ⎢⎣ ⎡ −= −= ∆−≈∆ ∫ c. Luas daerah yang dicari :
- 15. ( ) [ ] ( ) ( ) 3 2 0 3 2 3 2 2 0 2 0 22 0 2 3 2 2 0 22 2 2 2 2 51.33 3 8 802 3 44 3 2 2 4422 4422 141 satuan y yy y dyydydyy dyyy dyyV ≈ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ −+=⎥ ⎦ ⎤ ⎢ ⎣ ⎡ −+−−= ⎥⎦ ⎤ ⎢⎣ ⎡ −+−= −+−= ⎥⎦ ⎤ ⎢⎣ ⎡ −−+= ∫ ∫∫ ∫ ∫− ππ π π π c. Metode Kulit Tabung. Sebuah kulit tabung adalah sebuah benda yang dibatasi oleh dua tabung lingkaran tegak yang sumbu simetrinya berimpit, gbr. disamping. r1= jari-jari tabung dalam r2= jari-jari tabung luar h = tinggi tabung
- 16. maka volume tabung adalah : V = ( luas alas ) . ( tinggi) ( ) )( 2 2 .)()(. 12 12 1212 2 1 2 2 rrh rr hrrrrhrr −⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ + = −+=−= π πππ ∴ V = 2π x (jari-jari rata-rata)x(tinggi)(tebal) rrhV ∆= π2 atau untuk lebih mudahnya perhatikan gambar dibawah ini : Dari proses ini dapat dihitung sebuah benda putar kulit tabung. Gb. dibawah menunjukkan proses tersebut potongan jalur-jalur vertikal diputar mengelilingi sumbu y.
- 17. Contoh 1 : Tentukan volume benda yang terbentuk pada daerah yang dibatasi oleh kurva x y 1= , sumbu x, garis x = 1 dan garis x = 4 diputar mengelilingi sumbu y . Penyelesaian : Harga y dari persamaan x y 1= bila dihitung dan ditabelkan maka akan menghasilkan grafik seperti gambar di atas. Sehingga : ∫= b a dxxfxV )(2π 3 4 1 2 3 4 1 2 1 4 1 32.29 3 28 1. 3 2 8. 3 2 2 3 2 2 2 1 2 satuan x dxx dx x xV ≈ = ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ −= ⎥⎦ ⎤ ⎢⎣ ⎡ = = = ∫ ∫ π π π π π
- 18. Contoh 2 Daerah yang dibatasi oleh garis xhry )/(= , sumbu x dan garis x=h diputar mengelilingi sumbu x. Diperoleh sebuah kerucut (diandaikan 0,0 >> hr ). Tentukan volume kerucut itu dengan menggunakan metode cakram dan metode kulit tabung. Penyelesaian : 1. Metode Cakram : 32 2 32 0 3 2 2 0 2 2 2 0 2 2 2 2 3 1 3 3 satuanhr h hr x h r dxx h r dxx h r V xx h r V h h h π π π π π π = = ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ = = = ∆⎟ ⎠ ⎞ ⎜ ⎝ ⎛ ≈∆ ∫ ∫
- 19. 2. Metode Kulit tabung. 32 22 0 32 0 2 0 3 1 32 2 32 2 1 22 2 satuanhr rr h r yy h dyy r yhdyy r h hyV yy r h hyV r rr π ππ ππ π = ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ −=⎥ ⎦ ⎤ ⎢ ⎣ ⎡ −= ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ −=⎟ ⎠ ⎞ ⎜ ⎝ ⎛ −= ∆⎟ ⎠ ⎞ ⎜ ⎝ ⎛ −≈∆ ∫∫ 6. Volume benda dengan Penampang Lintang yang diketahui: Metode ini membahas benda yang memiliki daerah-daerah lingkaran sebagai penampang-penampang tegak yang berbentuk bujur sangkar atau segitiga. Jika luas penampang silang ABC, yang terjadi oleh suatu bidang tegak lurus pada sumbu-x dan berjarak x satuan dari titik asal, dapat dinyatakan sebagi fungsi x, A(x), maka volume benda diberikan oleh ∫= b a dxxAV )(
- 20. Contoh 1 : Sebuah benda mempunyai lingkaran alas yang berjari-jari 4 satuan. Cari volume benda itu, jika setiap bidang irisan tegak lurus pada garis tengah yang tetap, merupakan segitiga sama sisi. Penyelesaian : Ambil lingkaran seperti gambar di bawah dengan sumbu-x sebagai garis tengah tetap. Persamaan lingkarannya : .1622 =+ yx Penampang melintang ABC merupakan segitiga sama sisi dengan sisi 2y dan luas )16(33)( 22 xyxA −== . Maka : 3 4 0 2 4 0 2 4 4 2 3 3 256 3 16 4832 3 1632)16(32 )16(3)( satuan x xdxx dxxdxxAV b a =⎥⎦ ⎤ ⎢⎣ ⎡ −= ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ −=−= −== ∫ ∫∫ −
- 21. Contoh 2 : Alas sebuah benda adalah suatu daerah rata pada kuadran pertama yang dibatasi oleh 4/1 2 xy −= , sumbu-x dan sumbu-y. Andaikan penampang-penampang yang tegak lurus pada sumbu x berbentuk bujur sangkar. Tentukan volume benda ini. Penyelesaian. Bila dipotong-potong benda tegak lurus pada sumbu-x akan diperoleh lempengan tipis sbb: 3 2 0 53 2 0 42 07.1 15 16 80 32 6 8 2 806 162 1 satuan xx x dx xx V ≈= +−= ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ +−= ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ +−= ∫
- 22. 7. Panjang Kurva Misalkan P adalah titik (x, y) dan Q adalah titik pada kurva di dekat P. Misalkan pula sδ = panjang busur kecil PQ. Dari rumus phitagoras diberikan : ( ) ( ) ( )222 yxs δδδ +≈ Jika masing-masing ruas dibagi dengan 2 xδ , maka ( ) ( ) ( ) ( )2 2 2 2 1 x y x s δ δ δ δ +≈∴ 22 1 ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ +≈⎟ ⎠ ⎞ ⎜ ⎝ ⎛ ∴ x y x s δ δ δ δ ⎪⎭ ⎪ ⎬ ⎫ ⎪⎩ ⎪ ⎨ ⎧ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ +≈∴ 2 1 x y x s δ δ δ δ jika δx→0 ⎪⎭ ⎪ ⎬ ⎫ ⎪⎩ ⎪ ⎨ ⎧ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ += 2 1 dx dy dx ds ∫ ⎪⎭ ⎪ ⎬ ⎫ ⎪⎩ ⎪ ⎨ ⎧ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ +=∴ b a dx dx dy s 2 1
- 23. Contoh : Tentukan panjang kurva 32 xy = di antara x = 0 dan x = 4, untuk cabang y > 0. Penyelesaian : ∫ ⎪⎭ ⎪ ⎬ ⎫ ⎪⎩ ⎪ ⎨ ⎧ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ +=∴ b a dx dx dy s 2 1 32 xy =∴ 2 3 xy =→ , 2 3 2 3 x dx dy =∴ , 4 9 11 2 x dx dy +=⎟ ⎠ ⎞ ⎜ ⎝ ⎛ +∴ ∫ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ +=∴ 4 0 2 1 4 9 1 dx x s = 4 0 2 3 4 9 1 9 4 . 3 2 ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ + x [ ] [ ] 07.9162.31 27 8 11010 27 8 =−=−= satuan Panjang Kurva - persamaan parametrik. δt→0, bentuk ini menjadi : 222 ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ +⎟ ⎠ ⎞ ⎜ ⎝ ⎛ =⎟ ⎠ ⎞ ⎜ ⎝ ⎛ ∴ dt dy dt dx dt ds → ⎪⎭ ⎪ ⎬ ⎫ ⎪⎩ ⎪ ⎨ ⎧ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ +⎟ ⎠ ⎞ ⎜ ⎝ ⎛ =∴ 22 dt dy dt dx dt ds ∫ = = ⎪⎭ ⎪ ⎬ ⎫ ⎪⎩ ⎪ ⎨ ⎧ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ +⎟ ⎠ ⎞ ⎜ ⎝ ⎛ =∴ 2 1 22 tt tt dt dy dt dx s dt Misalkan )(),( tFxtfy == Dari rumus sebelumnya : ( ) ( ) ( )222 yxs δδδ +≈ bila kedua ruas dibagi dengan 2 xδ didapat, 222 ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ +⎟ ⎠ ⎞ ⎜ ⎝ ⎛ ≈⎟ ⎠ ⎞ ⎜ ⎝ ⎛ ∴ t y t x t s δ δ δ δ δ δ
- 24. Contoh : Tentukan panjang kurva θθ 33 sin2,cos2 == yx diantara titik-titik yang bersesuaian dengan θ = 0 dan θ = π/2. Penyelesaian: Menggunakan rumus yang sesuai dengan parameter, θ θθ π d d dy d dx s ∫ ⎪⎭ ⎪ ⎬ ⎫ ⎪⎩ ⎪ ⎨ ⎧ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ +⎟ ⎠ ⎞ ⎜ ⎝ ⎛ =∴ 2/ 0 22 Bila, θ3 cos2=x θθθθ θ sincos6)sin(cos6 22 −=−=→ d dx θθ θ θ cossin6sin2 23 =→= d dy y ∴ 22 ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ +⎟ ⎠ ⎞ ⎜ ⎝ ⎛ θθ d dy d dx = θθθθ 2424 cossin36sincos36 + = ( )θθθθ 2222 sincoscossin36 + = θθ 22 cossin36 θθθ θθ 2sin3cossin6 22 ==⎟ ⎠ ⎞ ⎜ ⎝ ⎛ +⎟ ⎠ ⎞ ⎜ ⎝ ⎛ ∴ d dy d dx maka didapatkan : satuan ds 3 2 1 2 1 3 2 2cos 3 2sin3 2 2 0 0 =⎥ ⎦ ⎤ ⎢ ⎣ ⎡ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ −−⎟ ⎠ ⎞ ⎜ ⎝ ⎛ = ⎥⎦ ⎤ ⎢⎣ ⎡− = =∴ ∫ π π θ θθ
- 25. 8. Luas Permukaan Benda Putar. Luas Permukaan yang terbentuk oleh perputaran busur y=f(x), suatu kurva kontinu, sekeliling sebuah garis yang sebidang (sumbu). Bila kurva diputar pada sumbu x diantara x=x1 dan x=x2 maka luas permukaan dapat ditentukan dengan rumusan sbb: Untuk menghitung luas pemukaan ini maka perlu dipenggal-penggal seperti gambar berikut : jika δx 0→ , maka dx ds y dx dA π2≈ Sebagaimana diketahui pada perhitungan panjang kurva, dimana ⎪⎭ ⎪ ⎬ ⎫ ⎪⎩ ⎪ ⎨ ⎧ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ += 2 1 dx dy dx ds , maka ⎪⎭ ⎪ ⎬ ⎫ ⎪⎩ ⎪ ⎨ ⎧ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ +π= 2 12 dx dy y dx dA Maka, dx dx dy yA x x∫ ⎪⎭ ⎪ ⎬ ⎫ ⎪⎩ ⎪ ⎨ ⎧ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ += 2 1 2 12π Jika sebuah elemen busur se-panjang δs satuan diputarkan, maka akan diperoleh sebuah pita tipis seluas δA. Didapat syA δπδ .2≈ Dengan membagi kedua rumus di atas dengan δx, didapatkan x s y x A δ δ π δ δ 2≈
- 26. Contoh : Tentukan luas permukaan yang terjadi jika busur parabola xy 82 = , dengan 0>y , di antara x = 0 dan x = 2 diputarkan mengelilingi sumbu x. Penyelesaian : ∴ dx dx dy yA ∫ ⎪⎭ ⎪ ⎬ ⎫ ⎪⎩ ⎪ ⎨ ⎧ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ += 2 0 2 12π ∴ xy 82 = 2 1 22 xy =⇒ ⇒ xdx dy x dx dy 2 2 2 2 1 =⎟ ⎠ ⎞ ⎜ ⎝ ⎛ ⇒= − ∴ x x xdx dy 22 11 2 + =+=⎟ ⎠ ⎞ ⎜ ⎝ ⎛ + ∴ dx x x xA ∫ ⎪⎭ ⎪ ⎬ ⎫ ⎪⎩ ⎪ ⎨ ⎧ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ + = 2 0 2 2 222 2 1 π dx x x x∫ + = 2 0 2 1 2 1 2 1 )2( ..24 π dxx∫ += 2 0 2 1 )2(.24 π 2 0 2/3 )2( .24 2 3 ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ + = x π = ( ) ( )[ ]228 3 28 − π [ ] [ ]312.7 3 8 428 3 8 π =− π = = 61.3 satuan3
- 27. Persamaan Parametrik Permukaan Putaran Jika busur kecil diputarkan sepanjang δs, maka luas δA pita kecil yang terbentuk diberikan oleh, syA δπδ .2≈ Kedua ruas dibagi dengan δt, diperoleh t s y t A δ δ π δ δ .2≈ Jika δt→0, hubungan ini menjadi dt ds y dt dA .2π≈ tinjau lagi persamaan panjang kurva parametrik, ⎪⎭ ⎪ ⎬ ⎫ ⎪⎩ ⎪ ⎨ ⎧ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ +⎟ ⎠ ⎞ ⎜ ⎝ ⎛ =∴ 22 dt dy dt dx dt ds maka, ⎪⎭ ⎪ ⎬ ⎫ ⎪⎩ ⎪ ⎨ ⎧ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ +⎟ ⎠ ⎞ ⎜ ⎝ ⎛ =∴ 22 2 dt dy dt dx y dt dA π dt dt dy dt dx yA ∫ ⎪⎭ ⎪ ⎬ ⎫ ⎪⎩ ⎪ ⎨ ⎧ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ +⎟ ⎠ ⎞ ⎜ ⎝ ⎛ =∴ 2 1 22 2 θ θ π Contoh : Tentukan luas pemukaan yang terbentuk jika busur kurva 22 3,3 ttxty −== di antara 0=t dan 1=t diputarkan mengelilingi sumbu OX sebanyak 2π radian. Penyelesaian : 2 2 2 3663 t dt dy t dt dy ty =⎟ ⎠ ⎞ ⎜ ⎝ ⎛ →=→=∴ ( )223 13333 tt dt dx ttx −=−=→−=∴ ( )42 2 219 tt dt dx +−=⎟ ⎠ ⎞ ⎜ ⎝ ⎛ ∴
- 28. 242 22 369189 ttt dt dy dt dx ++−=⎟ ⎠ ⎞ ⎜ ⎝ ⎛ +⎟ ⎠ ⎞ ⎜ ⎝ ⎛ ( ) dtttA ∫ ++=∴ 1 0 222 1932π ( ) ( )∫ ∫ +=+= 1 0 1 0 4222 18118 dtttdttt ππ 5 48 15 8 18 5 1 3 1 18 53 18 1 0 52 π πππ ==⎥⎦ ⎤ ⎢⎣ ⎡ +=⎥ ⎦ ⎤ ⎢ ⎣ ⎡ + tt satuan2 9. Momen, Pusat Masa (Titik Berat) Dua massa, masing-masing sebesar m1 dan m2 yang diletakkan pada papan seimbang dan berjarak d1 dan d2 dari titik penyangga pada bagian- bagian berbeda (lihat gambar) m1 m2 d1 d2 m1 m2 0 m x Syarat keseimbangan adalah M = 0. m1 m2 m3 m4 mn-1 mn x1 x2 0 x3 x4 xn-1 xn Jika koordinat titik seimbang x, dimana momen sistem terhadap titik ini harus nol, berapa koordinat x titik seimbang ? ( ) ( ) ( ) 0...2211 =−++−+− nn mxxmxxmxx Rumus seimbang : 2211 mdmd = Jika bandmil berimpit dengan titik asal maka, koordinat x1 dari m1 ada-lah x1=-d1 dan dari m2 adalah 22 dx = maka diberikan, 02211 =+ mxmx Hasilkali massa m dan jarak berarah dari suatu titik tertentu dinamakan momen. ∑ = =+++= n i iinn mxmxmxmxM 1 2211 ...
- 29. atau nnn mxmxmxmxmxmx +++=+++ ...... 212211 maka diperoleh ∑ ∑ = = == n i i n i ii m mx m M x 1 1 Distribusi massa yang kontinu pada suatu garis ∆x 0 a b Maka momen M terhadap titik asal : ∫ ∫== b a b a x xx m M x )( )( δ δ Distribusi massa pada Bidang Perhatikan n massa titik nmmm ,...,, 21 yang terletak pada titik-titik ( ) ( ) ( )nn yxyxyx ,,...,,,, 2211 pada bidang yang memiliki sebuah sistem koordinat pada gambar di bawah. 1m ),( 33 yx 3m ),( nn yx ),( 33 yx ),( 22 yx 2m ),( 11 yx Ini dinamakan pusat masa, titik dengan koordinat x ini adalah titik seimbang yang diperoleh sebagai hasil bagi momen sistem terhadap titik asal dan jumlah massa. Jika kepadatan di x adalah δ(x) dgn aturan “potong,hampiri, integral” maka, xxm ∆≈∆ )(δ xxxM ∆≈∆ )(δ ∫= b a dxxm )(δ ∫= b a dxxxM )(δ 4m ),( 44 yx Jumlah momen yM dan xM masing- masing terhadap sumbu x dan sumbu y ditentukan sbb: ∑ = = n i iiy mxM 1 ∑ = = n i iix myM 1
- 30. Koordinat-koordinat yx, titik berat sistem tersebut adalah ∑ ∑ = = == n i i n i ii y m mx m M x 1 1 ∑ ∑ = = == n i i n i ii x m my m M y 1 1 Mencari pusat massa (titik berat) sepotong lempeng tipis yang rata dengan menganggap lempengan tipis (lamina) homogen, berarti kepadatan δ adalah konstan. Untuk suatu lempengan homogen siku empat pusat masa berimpit dengan pusat geometrinya seperti gambar di bawah ini. Sepotongan lamina(lempengan tipis) homogen yang dibatasi oleh )(,, xfybxax === dan )(xgy = , dengan )()( xfxg ≤ . Potonglah lamina ini menjadi jalur-jalur yang sejajar dengan sumbu y seperti gambar di bawah. Jalur ini dapat dianggap berbentuk segi empat, sehingga massa masing-masing jalur dapat dianggap terpusat pada geometri padanya.
- 31. Kemudian hapirilah dan akhirnya jika 0→∆x maka dapat dintegralkan. [ ] xxgxfm ∆−≈∆ )()(δ [ ]dxxgxfm b a∫ −= )()(δ [ ] xxgxfxM y ∆−≈∆ )()(δ [ ]dxxgxfxM b ay ∫ −= )()(δ [ ] xxgxf xgxf Mx ∆− + ≈∆ )()( 2 )()( δ [ ]dxxgxfxM b ax ∫ −= )()( 2 22δ Dengan cara ini akan dihasilkan koordinat titik berat yx, yaitu m M x y = , m M y x = Maka, m M x y = [ ] [ ] [ ] [ ]dxxgxf dxxgxfx dxxgxf dxxgxfx b a b a b a b a ∫ ∫ ∫ ∫ − − = − − = )()( )()( )()( )()( δ δ [ ] [ ] [ ] [ ]dxxgxf dxxgxf dxxgxf dxxgxf m M y b a b a b a b ax ∫ ∫ ∫ ∫ − − = − − == )()( )()( 2 1 )()( )()( 2 2222 δ δ
- 32. Contoh : Tentukan sentroid (titik berat) daerah yang dibatasi 3 xy = dan xy = . Penyelesaian : 1. Mencari batas integral : ∴ xx =3 ⇒ 03 =− xx ⇒ 06 =− xx ∴ 1;0 21 == xx Dengan memasukkan nilai x pada persamaan 3 xy = dan xy = sehingga sketsa grafik didapat sebagai berikut : 2. Titik sentroid x [ ] [ ]dxx dxxxx ∫ ∫ − − = 1 0 3 1 0 3 3 = 1 0 4 2/3 1 0 5 2/5 43 2 55 2 ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ − ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ − x x x x = 12 5 5 1 = 25 12 ( ) ( )[ ] [ ]dxx dxx y ∫ ∫ − − = 1 0 3 1 0 232 3 3 2 1 = [ ] [ ]dxx dxxx ∫ ∫ − − 1 0 3 1 0 6 3 2 1 7 3 12 5 28 5 12 5 722 1 1 0 72 == ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ − = xx Titik centroidnya : );( 7 3 25 12C C
- 33. 10. Pusat Gravitas suatu benda putaran Untuk mencari posisi pusat gravitasi suatu benda yang terbentuk jika bentuk bidang yang dibatasi oleh kurva )(xfy = , sumbu x , dan ordinat pada ax = dan bx = diputarkan mengelilingi sumbu x. Contoh : Tentukan posisi pusat gravitasi dari benda yang terbentuk jika bidang yang dibatasi oleh kurva 1622 =+ yx , sumbu x, dan ordinat pada x = 1dan x = 3 diputar mengelilingi sumbu x. Penyelesaian : ∫ ∫=∴ 3 1 2 3 1 2 dxy dxxy x , 0=y ∫∫∫ −=−=∴ 3 1 33 1 23 1 2 )16()16( dxxxdxxxdxxy ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ −−⎟ ⎠ ⎞ ⎜ ⎝ ⎛ −=⎥ ⎦ ⎤ ⎢ ⎣ ⎡ −= 4 1 8 4 81 72 4 8 3 1 4 2 x x 442064 =−= ∫∫ −=∴ 3 1 23 1 2 )16( dxxdxy ( ) ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ −−−=⎥ ⎦ ⎤ ⎢ ⎣ ⎡ −= 3 1 16948 3 16 3 1 3 x x 3 1 23= 89.1 3 1 23 44 ==∴ x ; koordinatnya pusat gravitasi adalah : ( )0;89.1 Dari piringan-piringan elementer dijumlahkan momen volumenya (massanya) terhadap sumbu OY, maka dapat dihitung x , yaitu ∫ ∫= b a b a dxy dxxy x 2 2 , 0=y
